AP Syllabus focus:
‘Identify from tables when a limit does not exist, such as when values grow without bound, oscillate between several values, or approach different values from each side.’
Understanding when a limit fails to exist from a numerical table requires recognizing distinctive patterns in function values that reveal divergence, oscillation, or disagreement between directional approaches.
Recognizing When Numerical Tables Indicate a Nonexistent Limit
Tables of values are a powerful numerical tool for estimating limits, but they also reveal situations where a limit does not exist at a point. When studying limits numerically, AP Calculus AB students must learn to identify specific patterns in tables that signal the absence of a single value the function approaches. These patterns typically fall into three categories: unbounded behavior, oscillatory behavior, and inconsistent one-sided behavior. Each reflects a fundamental way in which a limit can fail to exist.
One-Sided Behavior and the Need for Agreement
A limit at a point requires both the left-hand limit and right-hand limit to approach the same number. A table approximates this by displaying function values as x approaches a target value from below and above. If these sequences behave differently, the limit does not exist.
Limit Does Not Exist (DNE): A limit fails to exist when the function values do not approach a single real number as the input approaches a point.
When interpreting tables, look for whether the values approaching from each side stabilize around a shared number. If patterns diverge, the limit is nonexistent.
Pattern 1: Approaching Different Values from Each Side
This pattern occurs when values approaching the target point from the left appear to settle near one number, while values from the right settle near a different number. Such disagreement indicates a jump in behavior and makes a single limit impossible.
Key Indicators
• Left-hand values cluster around a particular value.
• Right-hand values cluster around a different value.
• The gap between the two clusters does not shrink as the table narrows.
Why This Signals Nonexistence
A limit requires the function’s nearby values to compress toward the same output. If two distinct trends persist, no amount of zooming in will reconcile them.
Pattern 2: Unbounded Behavior in Table Values
Sometimes a table shows that as x approaches a target value, the corresponding function values increase or decrease without bound. This suggests the presence of infinite limits, which the syllabus identifies as a reason a limit may not exist in the real-number sense.
Unbounded Behavior: A function exhibits unbounded behavior near a point when its values grow arbitrarily large in the positive or negative direction as the input approaches that point.
A sentence separating definition blocks ensures clarity and flow when introducing essential calculus concepts.
How Tables Reveal Unbounded Growth
• Values increase rapidly with each step toward the target.
• The magnitude of the output shows no trend toward stabilization.
• Entries may switch sign or grow beyond the numerical scale of the table.
Implications
A limit that heads toward +∞ or −∞ does not settle at a finite number.
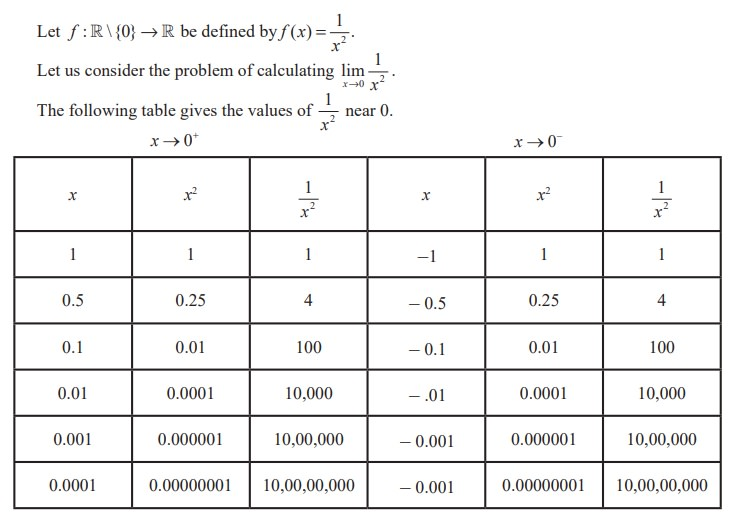
This table lists values of x approaching 0 from the right and left together with corresponding values of x² and 1/x². As the magnitude of x decreases, the 1/x² entries grow without bound, illustrating the unbounded table pattern. The surrounding text provides context for the function definition, extending slightly beyond the AP requirements but reinforcing how such tables are constructed. Source.
Pattern 3: Oscillatory Behavior
A table may also reveal oscillation, where values alternate between two or more outputs as x approaches a point. Oscillation prevents convergence and therefore prevents a limit from existing.
Oscillation: Repeated variation between two or more distinct values as inputs approach a point, preventing the output from approaching a single value.
A brief explanatory sentence reinforces the connection between oscillation and the failure of convergence.
How Oscillation Appears in a Table
• Values jump back and forth between multiple outputs rather than settling.
• The magnitude of the oscillation does not shrink as the table narrows.
• No numerical trend emerges toward a common number.
Why Oscillation Prevents Limits
A limit requires predictability and convergence. Oscillation demonstrates the opposite: values near the input point do not stabilize or cluster.
An oscillatory table pattern arises when values jump back and forth between several numbers (such as between values near 1 and near −1) without narrowing to a single target.
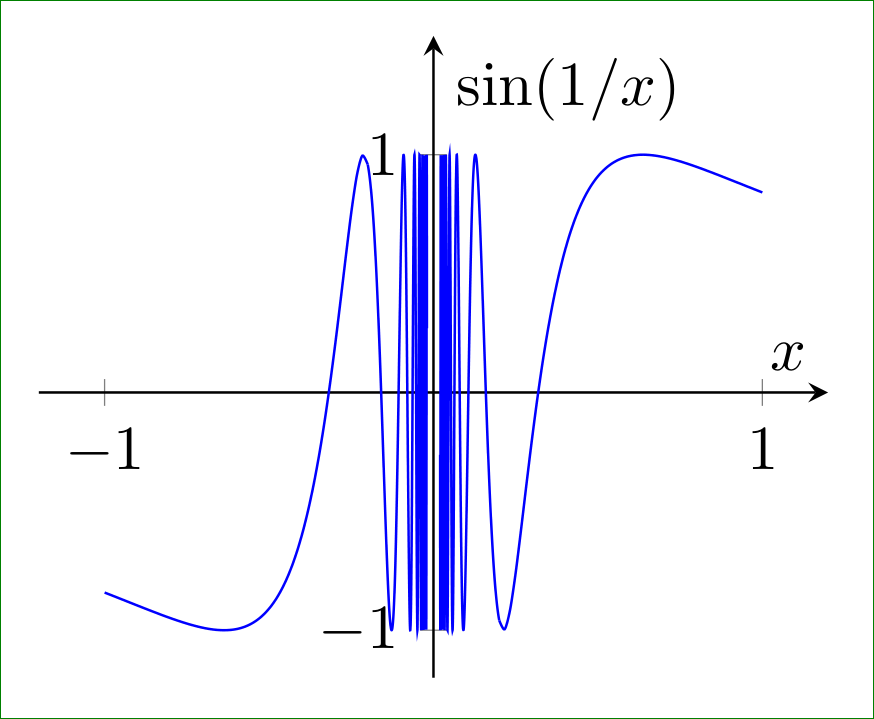
The graph of y = sin(1/x) shows increasingly rapid oscillations between 1 and −1 as x approaches 0. A numerical table created from this region would alternate between values near these bounds, never converging. The visual detail exceeds what appears in a table but directly supports the oscillatory limit-does-not-exist behavior described in the notes. Source.
The Importance of Recognizing Misleading Tables
Tables provide snapshots rather than continuous information, meaning misinterpretation is possible if the resolution is too coarse. A table with insufficient precision might hide oscillation or growing divergence. Therefore, when a limit appears not to exist, consider whether the table’s granularity is adequate to support the conclusion.
Key Considerations When Evaluating Tables
• Whether values are sampled close enough to the target.
• Whether both sides of the approach are represented.
• Whether repeated refinement shows stabilizing or destabilizing behavior.
Synthesizing Table Patterns with Limit Concepts
Recognizing when a limit does not exist from a table strengthens understanding of the underlying definition of limits. A limit requires all nearby paths to converge to a single value; any pattern suggesting divergence, disagreement, or instability indicates failure of that requirement. By identifying unbounded growth, oscillation, and directional mismatch in tables, students develop a robust ability to evaluate limits numerically in alignment with AP Calculus AB expectations.
FAQ
There is no fixed numerical threshold, but the values should be sufficiently close to the point of interest so that genuine patterns emerge.
In practice, when refining the table (for example, using increments of 0.1, then 0.01, then 0.001), the behaviour should become clearer. If divergence, oscillation, or disagreement persists despite refinement, this strongly suggests the limit does not exist.
Yes. Poorly rounded values may artificially create the illusion of oscillation or divergence.
Common issues include:
• Values rounded to too few decimal places.
• Differences appearing only because the table lacks precision.
• Apparent instability created when the true limit is very sensitive.
Using more accurate computations or checking values with technology reduces this risk.
A removable discontinuity affects only the function’s value at a single point, not the values near it.
Therefore, table entries still cluster around a common number on both sides. This means the table will look like a convergent limit scenario, even though the function itself is undefined or mismatched at the point.
Yes. If oscillations occur at a scale smaller than the table’s resolution, the pattern may not be visible.
This occurs when:
• The function oscillates infinitely often near the point.
• The table uses increments too large to capture rapid fluctuations.
Reducing step sizes helps reveal concealed oscillatory behaviour.
Look for a consistent trend rather than isolated large values.
Unbounded behaviour typically shows:
• Rapid escalation in magnitude with each refinement.
• No indication of stabilisation.
• Growth occurring on one or both sides of the target point.
If the large values fluctuate or remain within a limited band, the behaviour is extreme but not unbounded.
Practice Questions
Question 1 (1–3 marks)
A table of values for a function f is shown below as x approaches 2.
x: 1.9, 1.99, 1.999, 2.001, 2.01, 2.1
f(x): 3.2, 3.18, 3.179, 7.4, 7.39, 7.35
Using the table, determine whether the limit of f(x) as x approaches 2 exists. Justify your answer using numerical evidence.
Question 1 (3 marks total)
• 1 mark: States that the limit does not exist.
• 1 mark: Identifies that values approaching from the left (1.9 to 1.999) settle near approximately 3.18.
• 1 mark: Identifies that values approaching from the right (2.001 to 2.1) settle near approximately 7.37, showing disagreement.
Question 2 (4–6 marks)
A function g is investigated using a numerical table as x approaches 0. The table suggests the following behaviour:
• As x approaches 0 from the positive side, g(x) increases rapidly: 20, 50, 120, 300, ...
• As x approaches 0 from the negative side, g(x) decreases rapidly: -18, -47, -110, -290, ...
• A student concludes that the limit of g(x) as x approaches 0 does not exist.
(a) Explain, using the table behaviour, why the student claims the limit does not exist.
(b) Another student argues that because the values become large in magnitude, the limit must be infinite. Discuss whether this statement is correct, referring to the numerical pattern on both sides of 0.
(c) State clearly what conclusion should be drawn about the limit of g(x) as x approaches 0.
Question 2 (6 marks total)
(a) (2 marks)
• 1 mark: Recognises that values from the positive side grow without bound in the positive direction.
• 1 mark: Recognises that values from the negative side grow without bound in the negative direction.
(b) (2 marks)
• 1 mark: States that an infinite limit requires both sides to approach the same type of infinity.
• 1 mark: Notes that here one side tends to positive infinity while the other tends to negative infinity, so the criterion is not met.
(c) (2 marks)
• 1 mark: Correctly concludes that the limit does not exist as a real number.
• 1 mark: Clarifies that the limit also does not exist as an infinite limit because the one-sided behaviours diverge in opposite directions.

