The average rate of change describes how a function’s output varies with its input over an interval, providing a bridge between algebraic expressions and meaningful real-world interpretations.

Understanding Average Rate of Change

The average rate of change measures how much a function’s output changes relative to its input over a specific interval. This value helps describe overall behavior without requiring information about how the function behaves at every point. It is particularly useful when interpreting data or understanding a scenario where only initial and final information are available.

Because this quantity compares total change rather than moment-to-moment change, it conveys a broad trend rather than instantaneous behavior. Students should recognize that while the concept originates from algebraic difference quotients, its interpretation depends heavily on context.

Formal Structure of the Average Rate of Change

To compute an average rate of change, one compares values of the function at two input points. This structure supports consistent interpretation across formulas, graphs, and real-world situations.

This expression quantifies how much output changes per unit of input.

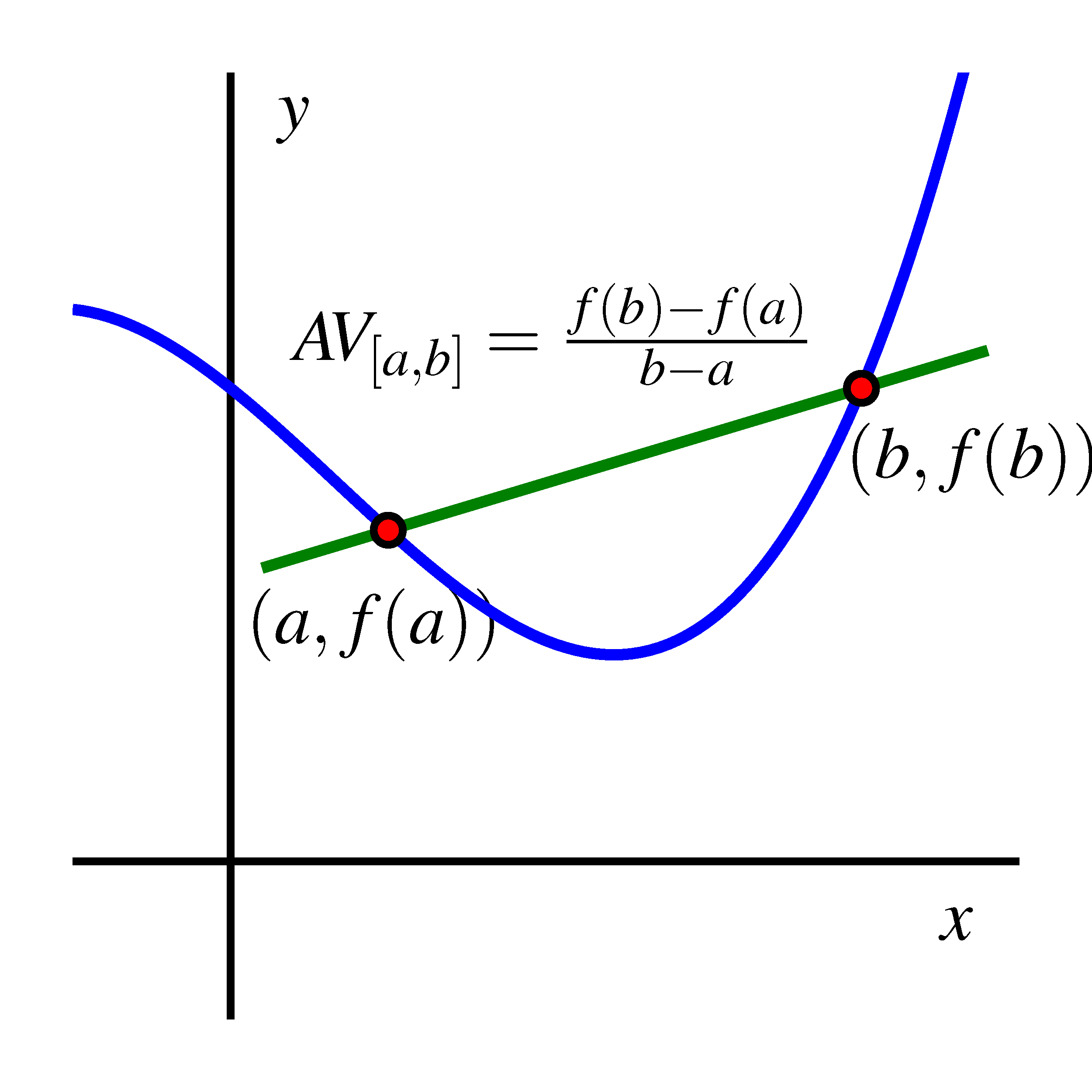
This figure shows a function with two highlighted points connected by a secant line. The slope $AV_{[a,b]} = \dfrac{f(b)-f(a)}{b-a}$ represents the average rate of change on the interval. The diagram emphasizes how total output change relates to total input change. Source.

A vital aspect of using this structure is recognizing the relationship between signs and meaning. A positive average rate of change indicates increasing behavior over the interval, while a negative value indicates decreasing behavior. A value of zero reveals no net change across the interval.

Interpreting Average Rate of Change in Formulas

When a function is given by a formula, students can apply algebraic substitution to evaluate $f(a)$ and $f(b)$ directly. This procedure allows precise computation and creates a foundation for interpreting the meaning of the result within real-world contexts.

Key interpretive skills include:

• Identifying the relevant interval based on the problem statement.

• Recognizing units of both input and output to determine the units of the average rate of change.

• Understanding how the magnitude of change communicates the strength of a relationship.

• Relating the result back to the modeled situation using clear, descriptive language.

Because the average rate of change captures overall behavior, it should not be misinterpreted as describing behavior at individual points inside the interval. Instead, it communicates the overall trend between the starting and ending values.

Important Terminology for Formula-Based Interpretation

Students should be comfortable with several key terms that frequently appear in problems involving function formulas:

• Interval: The pair of input values over which change is measured.

• Net change: The total difference in output between the two input points.

• Relative change: The output change compared to the input change, forming the essence of rate.

• Units of rate: Derived by dividing output units by input units, essential for correct contextual interpretation.

Each of these terms reinforces that average rate of change is fundamentally tied to how one quantity responds to changes in another.

Interpreting Average Rate of Change in Context

Real-world problems demand not only correct computation but also clear explanation of the meaning of the average rate of change. Typical contexts—such as motion, economics, population growth, or scientific measurement—rely on understanding what the function represents and how the interval selection affects interpretation.

To support meaningful interpretation in context, students should:

• Identify what the input represents in the scenario.

• Identify what the output represents in the scenario.

• State the rate using appropriate units from the context.

• Describe the average rate of change in words that match the real-world meaning of the function.

For instance, if input measures time and output measures distance, the resulting average rate of change carries the units of distance per time, describing overall speed over the interval.

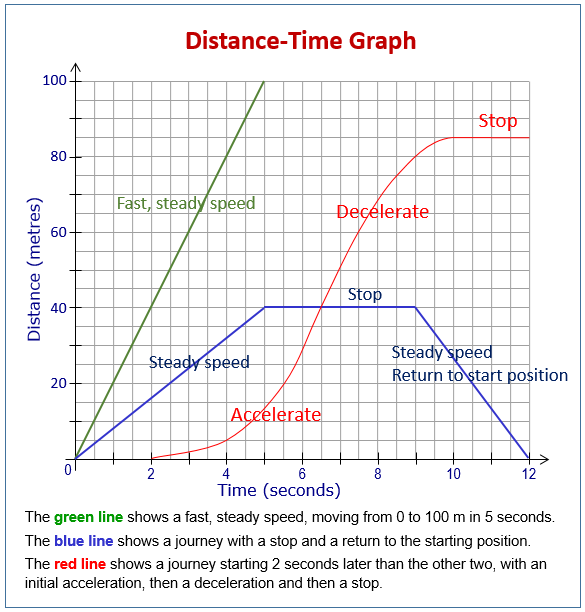
This graph illustrates how distance changes over time for different motion patterns. The slope of any segment, interpreted as $\dfrac{\text{change in distance}}{\text{change in time}}$, corresponds to an average speed. Additional labels such as “Accelerate” and “Steady speed” extend beyond the syllabus but help visualize varying rates of change. Source.

Common Interpretive Pitfalls

Students should avoid several misinterpretations that can distort the meaning of the average rate of change:

• Confusing average rate of change with instantaneous rate of change.

• Ignoring the context’s units when expressing the rate.

• Assuming behavior between the endpoints is uniform.

• Using interval endpoints incorrectly or reversing $a$ and $b$ in ways that alter sign and meaning.

Understanding these pitfalls ensures clearer communication and more accurate interpretation in applied settings.

Process for Interpreting and Communicating the Average Rate of Change

The following structure supports reliable interpretation across a wide variety of contexts:

• Identify the interval of interest based on the problem statement.

• Compute the net change in output and net change in input.

• Calculate the average rate of change using the difference quotient.

• Determine units by dividing output units by input units.

• Interpret the meaning of the computed value in complete sentences tied to the real-world situation.

This stepwise approach reinforces the connection between symbolic procedures and contextual understanding, fulfilling the syllabus requirement that students interpret average rates of change meaningfully across both formulas and real-world scenarios.