Derivatives of Secant and Cosecant Functions (2.10.2) | AP Calculus AB Notes

AP Syllabus focus:

‘Differentiate sec x and csc x by expressing them using cosine and sine, or using known formulas, and apply product and quotient rules as needed.’

This subsubtopic develops the differentiation of secant and cosecant functions by rewriting them in terms of sine and cosine or by applying established derivative rules to obtain efficient symbolic results.

Derivatives of Secant and Cosecant Functions

Understanding how to differentiate sec x and csc x expands the toolkit of trigonometric differentiation and reinforces the structural connections among trigonometric identities, algebraic manipulation, and derivative rules already learned. These derivatives frequently appear in applied settings and require fluency with both product and quotient representations of trigonometric functions.

Rewriting Secant and Cosecant Using Fundamental Trigonometric Identities

The functions sec x and csc x are reciprocals of cosine and sine. Introducing this relationship allows the derivative to be computed using familiar rules.

Secant Function: $\sec x = \dfrac{1}{\cos x}$ , the reciprocal of cosine.

A reciprocal form enables the use of the quotient rule or algebraic manipulation to prepare the expression for differentiation.

Cosecant Function: $\csc x = \dfrac{1}{\sin x}$ , the reciprocal of sine.

These identities guide the structure of the derivative and reveal how changes in cosine and sine influence changes in secant and cosecant.

Using the Quotient Rule When Differentiating Reciprocal Trigonometric Functions

Expressing sec x or csc x as a quotient highlights how the quotient rule produces characteristic combinations of trigonometric functions and their derivatives.

$\text{Quotient Rule: } \left(\dfrac{f}{g}\right)' = \dfrac{f'g - fg'}{g^{2}}$

$f$ = numerator function

$g$ = denominator function

A reciprocal function places the constant 1 in the numerator, producing derivatives driven almost entirely by the derivative of the denominator. This structure naturally leads to results involving squares of cosine or sine, which can then be rewritten using trigonometric identities to obtain standard derivative forms.

Because AP Calculus AB emphasizes conceptual preparation, students should recognize that differentiating a reciprocal triggers a negative sign and involves the derivative of the base trigonometric function.

Derivative of the Secant Function

To differentiate sec x efficiently, the function may be rewritten using a product identity. Since sec x can be expressed as $\sec x = \dfrac{1}{\cos x}$ , applying the quotient rule produces an expression that simplifies into a standard derivative formula used throughout calculus.

$\dfrac{d}{dx}(\sec x) = \sec x \tan x$

$\sec x$ = secant function

$\tan x$ = tangent function

This formula reflects how the reciprocal nature of secant combines with the derivative of cosine. The appearance of tan x is a natural consequence of rewriting negative ratios of sine and cosine. Students should recognize that the resulting product $\sec x \tan x$ reinforces the interconnected nature of trigonometric derivatives.

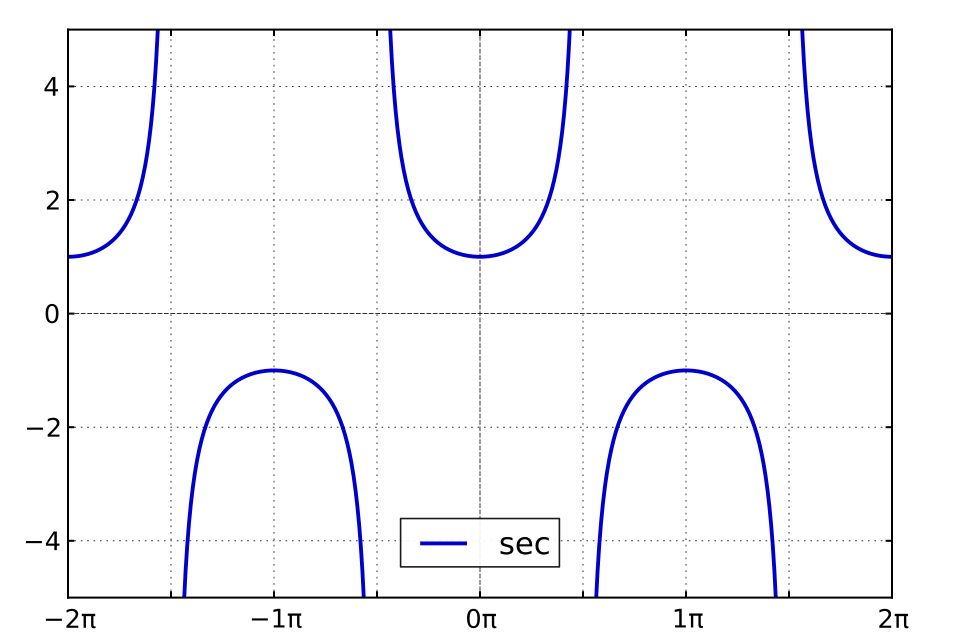
Graph of the secant function $y=\sec x$ over $[-2\pi,2\pi]$ , illustrating vertical asymptotes and steep growth where $\cos x$ approaches zero. This visualization supports interpreting the derivative $,\frac{d}{dx}(\sec x)=\sec x\tan x,$ in terms of rapidly changing slopes. Source.

Derivative of the Cosecant Function

Like secant, the cosecant function differentiates most cleanly when expressed as a reciprocal and simplified using known relationships among trigonometric functions.

$\dfrac{d}{dx}(\csc x) = -\csc x \cot x$

$\csc x$ = cosecant function

$\cot x$ = cotangent function

The negative sign originates from the derivative of sine, and the appearance of cot x emerges as the quotient of cosine and sine within the reciprocal structure. Understanding these relationships helps students build strong connections between derivative behavior and the geometry of the unit circle.

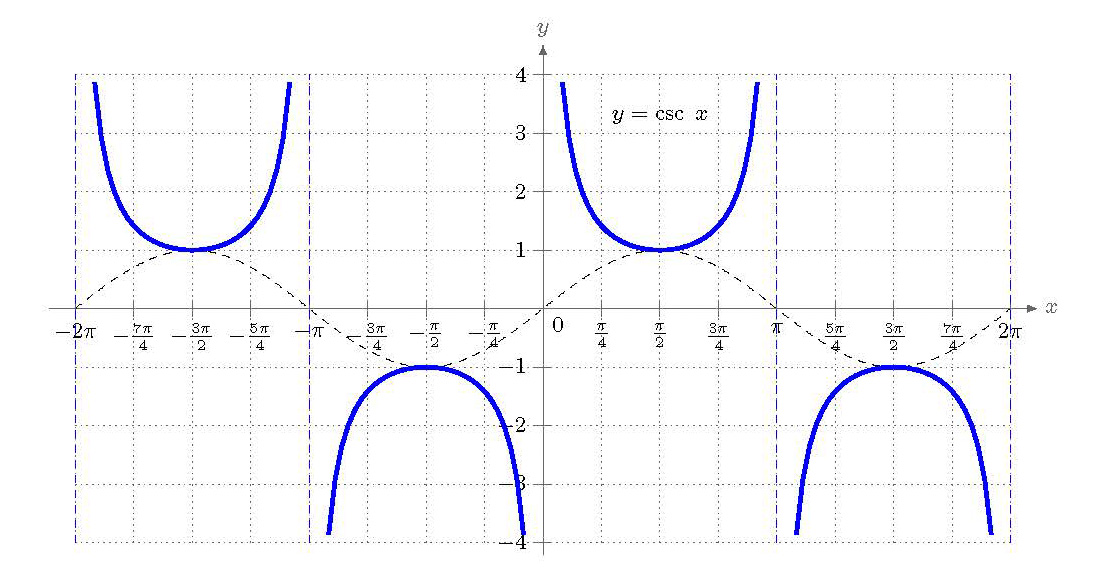
Graph of $y=\csc x$ with $y=\sin x$ shown as a dashed reference curve. The vertical asymptotes of $\csc x$ at zeros of $\sin x$ illustrate the reciprocal identity $,\csc x=\frac{1}{\sin x},$ . The sine curve is additional context beyond the syllabus but clarifies how the derivative relates to the underlying function. Source.

A key instructional objective is for students to see these results not as isolated formulas but as natural extensions of the reciprocal identities and the derivative rules already mastered. The presence of a product in both derivative formulas signals that even functions defined as reciprocals can yield derivatives expressed through products of trigonometric functions.

Applying Product and Quotient Rules Strategically

Students should be able to recognize situations in which rewriting a trigonometric expression before differentiating may significantly reduce algebraic complexity. The choice between applying a rule directly or manipulating the expression first depends on the goal of simplification.

Key considerations include:

Determining whether a reciprocal form or an identity involving sine and cosine leads to a cleaner derivative.
Recognizing when expressing a trigonometric function as a product supports straightforward differentiation.
Maintaining awareness that derivative expressions for sec x and csc x nearly always appear as products with tangent or cotangent, respectively.
Ensuring that signs and reciprocal relationships are handled accurately, especially when derivatives of sine and cosine introduce sign changes.

Conceptual Connections to Prior Derivative Rules

Understanding derivatives of sec x and csc x reinforces earlier concepts, including:

How derivative rules interact with reciprocal identities.
How the quotient rule structures derivative expressions before simplification.
How familiar trigonometric relationships create opportunities for algebraic rewriting that leads to standard derivative forms.

These conceptual ties strengthen students’ ability to generalize patterns within trigonometric differentiation and to apply derivative formulas flexibly across a range of mathematical and applied problems.

FAQ

The appearance of tangent and cotangent results from simplifying expressions that emerge when differentiating reciprocal trigonometric functions.

When sec x and csc x are rewritten in terms of sine and cosine, the derivative naturally produces ratios such as sin x divided by cos x or vice versa. These ratios correspond exactly to the definitions of tangent and cotangent.

Thus, tangent and cotangent are not added arbitrarily; they arise directly from algebraic simplification after applying derivative rules.

Both approaches work, but rewriting often leads to cleaner expressions and reduces the chance of sign errors.

The quotient rule can introduce multiple negative signs, especially when differentiating 1 over a trigonometric function. By rewriting the function using identities or expressing it as a product, the differentiation steps become more transparent.

In practice, most students find rewriting first more efficient and less error-prone.

The difference in sign stems from the derivatives of cosine and sine.

• The derivative of cosine is negative, creating a positive outcome when differentiating sec x.
• The derivative of sine is positive, but its reciprocal structure produces a negative coefficient when differentiating csc x.

These sign differences reflect the underlying behaviour of the parent functions rather than anything unique to secant or cosecant themselves.

The derivative is undefined exactly where the original function is undefined.

• Sec x is undefined where cos x = 0.
• Csc x is undefined where sin x = 0.

Since the derivative formulas include sec x or csc x as factors, any x-value that makes these expressions undefined also makes the derivative undefined. This corresponds to points where the functions have vertical asymptotes.

As sine or cosine approaches zero, their reciprocals (csc x and sec x) grow without bound, causing rapid vertical changes.

Because the derivatives of these functions include products with tangent or cotangent, the slopes also become extremely large near the same points.

This steepness reflects the sensitivity of reciprocal functions: very small changes in sine or cosine produce large changes in their reciprocals, and the derivative measures exactly how fast that change occurs.

Practice Questions

Question 1 (1–3 marks)
Differentiate the function f(x) = 5 sec x.
Give your answer in its simplest form.

Question 1 (1–3 marks)
• 1 mark: Correct use of the constant multiple rule.
• 1 mark: Correct derivative of sec x stated as sec x tan x.
• 1 mark: Final simplified answer f′(x) = 5 sec x tan x.

Total: 3 marks.

Question 2 (4–6 marks)
A function is defined by g(x) = sec x • csc x for values of x where both functions are defined.
(a) Show that g(x) can be rewritten in the form g(x) = 1 / (sin x cos x).
(b) Hence find g′(x).
(c) Using your answer to part (b), explain why g′(x) becomes undefined at x = π/2.

Question 2 (4–6 marks)

(a)
• 1 mark: Correctly stating sec x = 1 / cos x.
• 1 mark: Correctly stating csc x = 1 / sin x.
• 1 mark: Concluding g(x) = 1 / (sin x cos x).

(b)
• 1 mark: Correct method shown (e.g., product rule or differentiating reciprocal form).
• 1 mark: Correct derivative of sec x as sec x tan x.
• 1 mark: Correct derivative of csc x as –csc x cot x.
• 1 mark: Final correct expression for g′(x), such as:
g′(x) = sec x tan x csc x + sec x (–csc x cot x).

(c)
• 1 mark: Correct reasoning that sin x = 0 at x = π/2.
• 1 mark: Recognition that this makes g(x) and its derivative undefined because they involve division by sin x.

Total: 6 marks.

Try All Topic Practice Questions

Written by:

Dr Rahil Sachak-Patwa

Oxford University - PhD Mathematics

Rahil spent ten years working as private tutor, teaching students for GCSEs, A-Levels, and university admissions. During his PhD he published papers on modelling infectious disease epidemics and was a tutor to undergraduate and masters students for mathematics courses.