These notes develop how to differentiate tangent and cotangent functions by rewriting them using fundamental trigonometric identities and applying established derivative rules with clarity and precision.

Derivatives of Tangent and Cotangent Functions

Differentiating $\tan x$ and $\cot x$ is an essential skill in AP Calculus AB, and the syllabus emphasizes using trigonometric identities and quotient relationships to accomplish this efficiently. Because tangent and cotangent are defined in terms of sine and cosine, their derivatives naturally follow from combining the quotient rule, product rule, and known derivatives of $\sin x$ and $\cos x$. Understanding these relationships strengthens conceptual insight into how trigonometric functions change and prepares students for later applications in modeling and optimization.

Rewriting Tangent and Cotangent Using Fundamental Identities

The functions tangent and cotangent should first be recognized as ratios of sine and cosine. This rewriting is essential because it allows the direct use of previously learned derivative rules.

This identity reveals that tangent is a quotient of two differentiable trigonometric functions, allowing the derivative to be determined through the quotient rule.

Once this identity is established, differentiation proceeds by examining how both the numerator and denominator vary with respect to $x$. Before differentiating, it is helpful to note that the derivative of sine is cosine, and the derivative of cosine is negative sine. These relationships underpin every step in differentiating tangent.

Cotangent mirrors the structure of tangent but reverses the roles of sine and cosine.

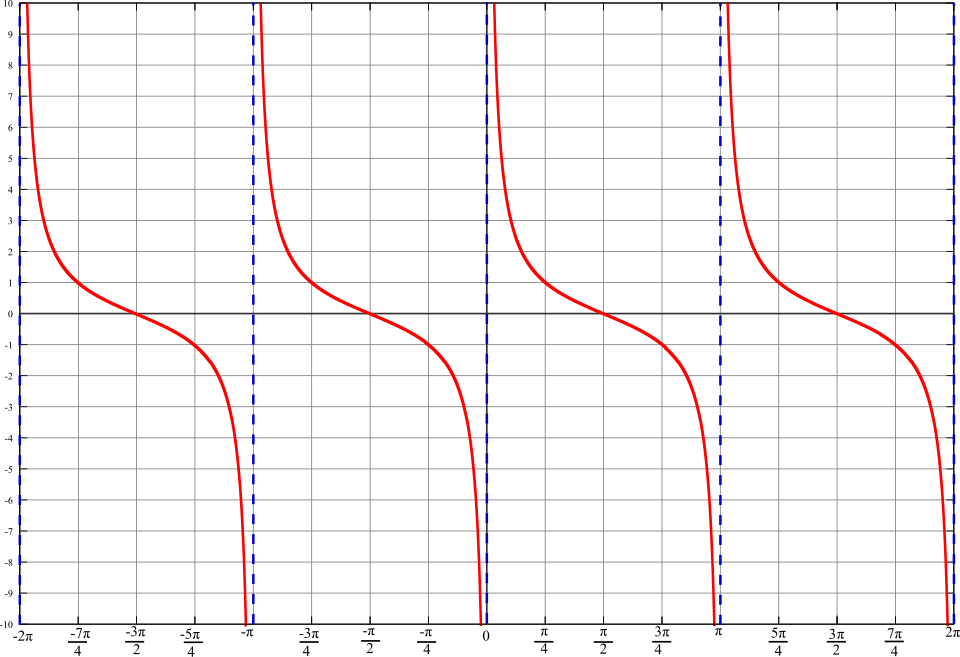
This graph shows $y = \cot x$ across several periods, illustrating its vertical asymptotes at multiples of $\pi$ and its decreasing behavior between them. The figure highlights how expressing cotangent as $\dfrac{\cos x}{\sin x}$ leads to its characteristic discontinuities. No additional curriculum-external content is included. Source.

This reversal leads to a different pattern in the resulting derivative. Because cotangent also involves division by a trigonometric expression, the quotient rule again becomes the primary tool for differentiation.

A clear understanding of these identity-based forms ensures that each derivative follows logically from rules already mastered.

Applying the Quotient Rule to Trigonometric Ratios

Once tangent and cotangent are expressed using sine and cosine, the quotient rule becomes the central technique for differentiation. Students should recall that the quotient rule examines how the numerator and denominator each change, measuring their combined effect on the overall ratio.

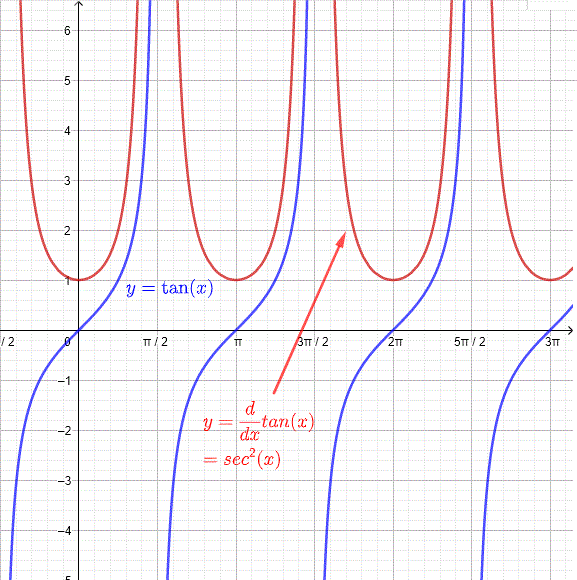
This graph displays $y = \tan x$ along with its derivative $y = \sec^2 x$, illustrating how the derivative grows sharply near tangent’s vertical asymptotes. The height of the $\sec^2 x$ curve corresponds directly to the steepness of the tangent function. This includes minor detail beyond core syllabus requirements but enhances conceptual understanding. Source.

This representation highlights how the quotient rule operates structurally. While this equation expresses the initial step in the derivative process, students ultimately simplify to the well-known formula involving secant. The appearance of squared trigonometric expressions and sign changes reflects how the sine and cosine derivatives contribute to the overall rate of change of tangent.

Before applying similar reasoning to cotangent, it is important to acknowledge that its numerator and denominator differ in order from those of tangent. The quotient rule will thus produce a change in sign and structure once simplified.

The resulting structure reveals how the derivative of cotangent depends on the combination of squared sine and cosine terms in the numerator and the squared sine function in the denominator. The presence of negative signs plays a crucial role in the final derivative expression.

Final Derivative Forms and Their Interpretive Meaning

From the processes shown above, the derivatives of tangent and cotangent simplify to their classical forms. These derivatives express how rapidly the trigonometric ratios change for a given angle. Because tangent and cotangent rapidly increase near odd multiples of $\dfrac{\pi}{2}$ or integer multiples of $\pi$, the derivatives naturally include expressions involving squared secant or cosecant functions that reflect steep slopes near vertical asymptotes.

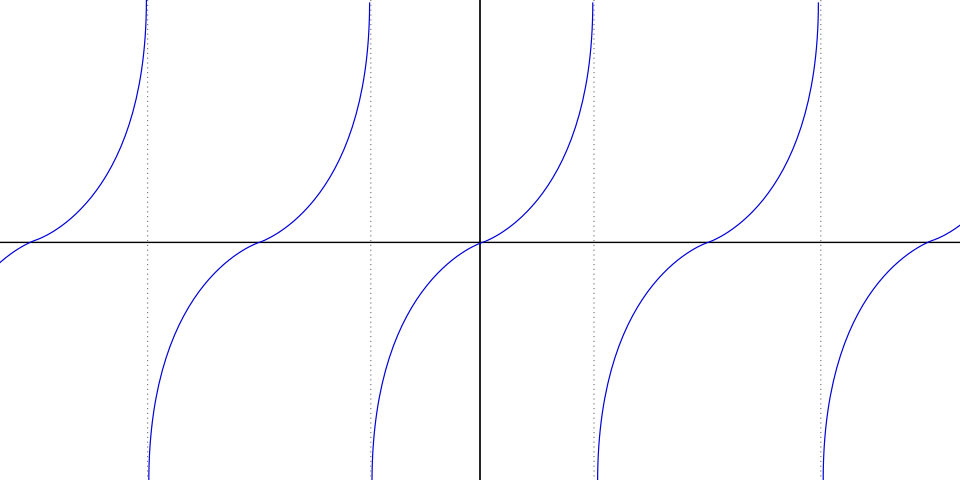
This image shows the graph of $y = \tan x$ with its characteristic vertical asymptotes at odd multiples of $\dfrac{\pi}{2}$. The curve’s steep behavior near these asymptotes visually supports the discussion of rapidly increasing derivative values. Labels and structure stay within the scope of AP Calculus AB expectations. Source.

Students should note the following key ideas:

• Tangent and cotangent derivatives result from combining quotient relationships with known trigonometric derivatives.

• Simplification typically introduces squared reciprocal identities such as $\sec^2 x$ and $\csc^2 x$.

• These derivatives capture how the rates of change behave near angles where sine or cosine approach zero, aligning with the shape of tangent and cotangent graphs.

Essential Takeaways for AP Calculus Learners

• Always rewrite tangent and cotangent as sine-cosine quotients before differentiating.

• Apply the quotient rule carefully, ensuring correct placement of derivatives of sine and cosine.

• Simplify expressions using familiar identities to reveal the standard derivative forms.

• Recognize that the resulting derivatives describe rapidly changing behavior near function asymptotes.