AP Syllabus focus:
‘Apply the inverse derivative formula to compute derivatives of inverse functions at given points, often using values from tables or graphs of f rather than an explicit f⁻¹.’
Understanding derivatives of inverse functions at specific points allows you to compute slopes of inverse curves efficiently, often without an explicit inverse formula, by leveraging known information about the original function.
Derivatives of Inverses at Specific Points
When working with inverse functions in calculus, one of the most powerful ideas is that the derivative of an inverse at a point can be determined using information about the original function rather than solving explicitly for the inverse. This subsubtopic focuses on computing such derivatives efficiently by applying the inverse derivative formula to specific numerical points, frequently using values from a table or graph.
Relationship Between a Function and Its Inverse
A function and its inverse swap the roles of inputs and outputs, which means the slopes of their graphs have a reciprocal relationship at corresponding points. Because evaluating or differentiating an inverse function directly is often difficult, AP Calculus students rely on the structural connection between the two functions.
Inverse Function: A function f⁻¹ such that f(f⁻¹(x)) = x and f⁻¹(f(x)) = x for all x in the domain where f is one-to-one.
This reciprocal nature allows us to use derivative information from the original function to determine the derivative of the inverse, even when the inverse is not explicitly expressed.
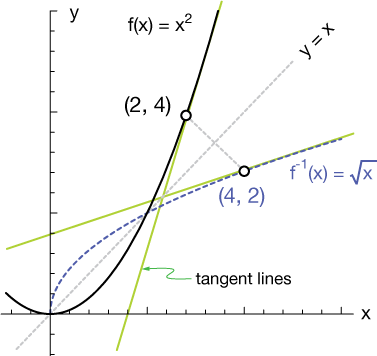
This figure shows a function and its inverse with tangent lines drawn at corresponding points. The slopes of these tangent lines are reciprocals, illustrating how derivative information from the original function determines the derivative of the inverse at a specific point. Source.
The Inverse Derivative Formula
The chain rule provides a direct path to the derivative of an inverse at a point. Applying the relationship f(f⁻¹(x)) = x yields a formula that connects the derivative of f⁻¹ with the derivative of f evaluated at a corresponding point.
( f⁻¹ )′(x) = 1 / f′( f⁻¹(x) )
( f⁻¹ )′(x) = Slope of the inverse function at input x
f′( f⁻¹(x) ) = Derivative of f evaluated at the point whose output equals x
Because the inverse derivative depends on f⁻¹(x), students often use tables or graphs to find the matching x-value on the original function without needing to compute the inverse algebraically.
A crucial step is recognizing that the point (a, b) on f corresponds to the point (b, a) on f⁻¹. This reversal of coordinates makes it possible to compute inverse derivatives using known function values.
Why We Use Values From Tables or Graphs
In many AP Calculus AB problems, the function f may not be given as a formula. Instead, you may be provided with:
A table showing x, f(x), and possibly f′(x)
A graph of f
A verbal description outlining key values of f and f′

This table provides values of a function and its derivative that can be used to compute derivatives of the inverse at specific points. By matching an output value to the table and taking the reciprocal of the listed derivative, the slope of the inverse can be determined without finding an explicit inverse formula. Source.
These representations allow you to locate the point where f(x) = a, identify the corresponding x-value (which becomes f⁻¹(a)), and then evaluate the derivative f′(f⁻¹(a)). The chain rule relationship ensures that information from f suffices to compute the slope of the inverse.
Key Ideas When Identifying Derivatives at Specific Points
To compute (f⁻¹)′(a) from available information, students must coordinate several conceptual steps that align with the inverse relationship:
Identify the corresponding point on f
Find the value x such that f(x) = a. This x becomes f⁻¹(a).Evaluate the derivative of f at this point
Determine f′(x) using provided derivative data or by interpreting the slope from a graph.Apply the inverse derivative formula
Take the reciprocal of that derivative to obtain (f⁻¹)′(a).Confirm that f′(x) ≠ 0
The derivative of the inverse exists only when the derivative of f at the corresponding point is nonzero, ensuring local invertibility.
Normal interpretation of the graph or table is essential, since correct identification of the matching x-value underlies the entire process.
Practical Structure for Solving These Problems
Though full examples are not included here, it is helpful to internalize a consistent structure for approaching point-specific inverse derivative questions. Students should:
Use given output values to locate the necessary input for f
Use given derivative information to compute f′(x)
Use inverse derivative reciprocity to compute (f⁻¹)′(a)
Emphasize the exchange of coordinates between f and f⁻¹
These steps mirror the AP requirement: you must be proficient at determining the slope of an inverse using only original function data, without needing an explicit inverse formula.
Importance Within the AP Curriculum
This topic prepares students to reason flexibly about functions and their inverses, including in problems that blend graphical and numerical representations. The AP Calculus AB framework emphasizes fluency in switching perspectives between a function and its inverse, understanding how their derivatives relate, and extracting needed information from limited or indirect sources. Mastery of these relationships enhances efficiency in later differentiation tasks and strengthens conceptual understanding of the chain rule as a unifying tool.
FAQ
If the required output value is not in the table, you cannot determine the exact derivative of the inverse using the table alone. AP-style questions only ask for (f⁻¹)'(x) when the corresponding value appears explicitly.
If the value is close to one in the table, you may be able to estimate, but such approximation tasks are rare in this subsubtopic and would be clearly indicated.
The derivative formula relies on the existence of a unique x-value satisfying f(x) = a. If f is not one-to-one, this correspondence fails.
A one-to-one function ensures:
• A unique input-output pairing
• A valid inverse function near the point of interest
• A meaningful reciprocal relationship between slopes
The slope of f⁻¹ at a point represents how steeply the inverse rises when x changes. Because inverse graphs reflect across the line y = x, their tangent lines also reflect.
This means:
• The slope of the inverse equals the reciprocal of the slope on the original function
• A steep slope on f becomes a shallow slope on f⁻¹, and vice versa
The essential first step is locating the point on f where the y-value equals a. Without identifying this matched point, the inverse derivative cannot be computed.
After locating the point:
• Determine the slope of f at that point
• Make sure the slope is non-zero
• Take the reciprocal to obtain the derivative of the inverse
A zero derivative indicates a horizontal tangent on f. At such a point, the graph fails the local invertibility requirement, because the reciprocal of zero is undefined.
This reflects that:
• A horizontal tangent would correspond to an infinitely steep tangent on the inverse
• The inverse function cannot have a well-defined derivative at that corresponding point
Practice Questions
(1–3 marks)
A function f is differentiable and one-to-one. A table of values is given:
f(2) = 5, f(4) = 9, f(7) = 12
f'(2) = 3, f'(4) = 6, f'(7) = 10
Find the value of (f⁻¹)'(9).
(1–3 marks)
• 1 mark for identifying that f⁻¹(9) corresponds to the x-value where f(x) = 9, which is x = 4.
• 1 mark for applying the inverse derivative rule: (f⁻¹)'(9) = 1 / f'(4).
• 1 mark for the correct numerical answer: 1/6.
Total: 3 marks.
(4–6 marks)
The function g is differentiable and strictly increasing. You are given the following information:
g(1) = 4, g(3) = 10, g(4) = 15
g'(1) = 2, g'(3) = 5, g'(4) = 12
(a) Explain how to identify the value of g⁻¹(10) using the information above.
(b) Hence calculate (g⁻¹)'(10).
(c) Briefly justify why the derivative of g⁻¹ exists at x = 10.
(4–6 marks)
(a) (1–2 marks)
• 1 mark for stating that to find g⁻¹(10), we locate the x-value where g(x) = 10.
• 1 mark for identifying that g(3) = 10, so g⁻¹(10) = 3.
(b) (2–3 marks)
• 1 mark for stating the inverse derivative rule: (g⁻¹)'(10) = 1 / g'(g⁻¹(10)).
• 1 mark for substituting g⁻¹(10) = 3, giving 1 / g'(3).
• 1 mark for the correct numerical answer: 1/5.
(c) (1 mark)
• 1 mark for stating that g'(3) is non-zero and g is one-to-one (or strictly increasing), ensuring that g is locally invertible and the derivative of its inverse exists.
Total: 6 marks.

