AP Syllabus focus:
‘Interpret derivatives of inverse functions as reciprocals of slopes on the original function and explain how this relationship can simplify differentiation problems.’
Interpreting Derivatives of Inverse Functions
Understanding how the derivative of an inverse function relates to the original function helps clarify why inverse differentiation often reduces to evaluating reciprocals of known slopes.
AP Calculus AB students frequently encounter functions whose inverses are difficult to write explicitly, yet their derivatives remain accessible. This topic highlights how slopes on a function and its inverse correspond through a reciprocal relationship, allowing efficient interpretation and computation of derivative values.
The Geometric Relationship Between a Function and Its Inverse
The graph of a function f and its inverse f⁻¹ are reflections across the line y = x. Reflecting a point on a graph exchanges its coordinates, and this symmetry plays a crucial role in understanding derivatives of inverses.
Slopes and the Line y = x
Because reflection swaps x and y, a slope on the original function transforms into the slope of the inverse at the corresponding reflected point. This motivates the central idea that steepness on one graph corresponds to reciprocal steepness on the other.
“On a graph, the curve of and the curve of are mirror images across the line .”
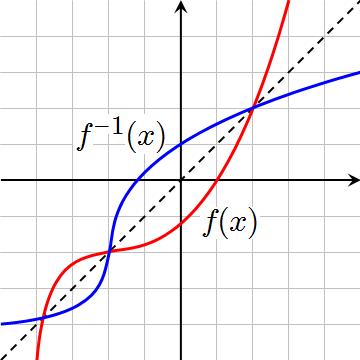
This graph shows and its inverse reflected across the line . Comparing corresponding points illustrates how inputs and outputs interchange under inversion. This geometric relationship underpins the interpretation of inverse derivatives. Source.
Reciprocal Slopes
When f is differentiable and f′ is nonzero at a point, the slope of f⁻¹ at the corresponding point is the reciprocal of the original slope. This connection explains why explicit formulas for inverses are often unnecessary for finding derivatives.
= Derivative of the original function
= Input value on the inverse corresponding to an output of
Interpreting the Reciprocal Relationship
The reciprocal nature of slopes reveals how the behaviors of paired functions mirror each other.
Meaning of the Reciprocal
If f′(a) is large, then (f⁻¹)′(f(a)) is small, indicating that a steep increase in the original function produces a gentle rise in the inverse at its associated point. Likewise, a small but nonzero slope in the original leads to a large slope in the inverse.
Importance of One-to-One Behavior
The reciprocal formula only applies when f is one-to-one, meaning it passes the horizontal line test. This ensures that each output corresponds to a single input, allowing the inverse to be a proper function.
One-to-One Function: A function for which every output value corresponds to exactly one input, guaranteeing the existence of an inverse function.
Because inverse derivatives depend on evaluating f′ at a specific matching point, the function must be invertible so that the relationship between corresponding points is well defined.
A sentence must appear here to maintain required spacing before another definition block.
Corresponding Point: For a point on a function , the corresponding point on is , obtained by reflecting across .
Using Slopes on the Original Function to Understand the Inverse
Students often interpret derivatives in graphical or tabular contexts. When explicit formulas are unavailable, the reciprocal relationship becomes especially valuable.
Graphical Interpretation
If a graph shows that f has a particular slope at a point, the slope of f⁻¹ at the reflected point can be interpreted directly:
A positive slope on f implies a positive slope on f⁻¹, preserving increasing behavior.
A negative slope on f implies a negative slope on f⁻¹, preserving decreasing behavior.
The steepness is inverted proportionally through a reciprocal.
“At corresponding points on and on , the tangent lines are reflections across , so their slopes are reciprocals of each other.”
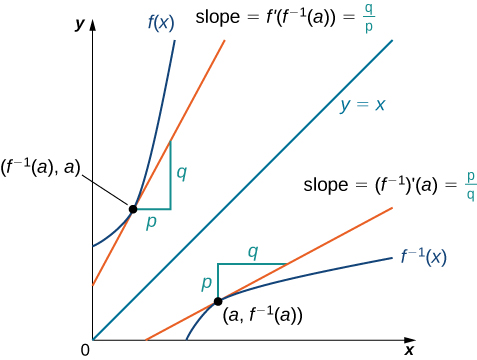
This illustration displays and together with tangent lines at reflected points. One tangent has slope and the other has slope , highlighting the reciprocal relationship between corresponding slopes. The image includes symbolic slope labels beyond the syllabus, but it accurately conveys the principle that . Source.
Tabular Interpretation
Tables frequently provide values of f, f′, and associated coordinate pairs. The reciprocal relationship allows the derivative of the inverse to be interpreted without ever computing f⁻¹ explicitly. Students locate the appropriate input on the original table, find its derivative, and take the reciprocal to interpret the slope of the inverse at the corresponding value.
Why the Reciprocal Formula Simplifies Problems
The key advantage of interpreting inverse derivatives lies in avoiding complex algebra. Many functions have inverses that are not elementary or involve cumbersome expressions. Instead of manipulating potentially complicated inverse forms, the reciprocal formula:
Reduces computation by using known derivatives of the original function.
Allows differentiation even when the inverse cannot be written explicitly.
Connects algebraic, numerical, and graphical reasoning through consistent slope relationships.
Reinforces the broader principle that reflecting a function across y = x interchanges roles of inputs and outputs.
Conceptual Summary of Interpretation Behaviors
To consolidate understanding of how inverse derivatives are interpreted, consider these essential ideas:
Reciprocal slopes form the heart of the interpretation of inverse derivatives.
Reflection across y = x provides the geometric justification.
Corresponding points link the evaluation of f′ to the derivative of f⁻¹.
Nonzero derivatives ensure that slopes remain defined and meaningful under inversion.
One-to-one behavior ensures that each output corresponds to a single input, maintaining a valid inverse function structure.
These interpretive tools equip students to approach inverse differentiation with confidence, especially when functions are represented graphically or numerically rather than through explicit formulas.
FAQ
Check that the function is one-to-one on the displayed interval. This usually means the graph is consistently increasing or consistently decreasing with no turning points.
Then identify the point where the slope is required. Once you know the slope of the original function at that point, the derivative of the inverse is simply the reciprocal of that slope.
If the graph is not one-to-one on the shown interval, the derivative of the inverse is not defined there.
A small slope on the original function means the graph is nearly horizontal, so a small change in output requires a large change in input.
When the axes are swapped for the inverse, this behaviour becomes a steep slope because the inverse graph must rise sharply to reflect the large input change.
This phenomenon is especially noticeable near flat sections of the original function.
As the original derivative approaches zero, the reciprocal becomes very large, so the inverse’s derivative tends to grow rapidly.
This indicates the inverse graph is becoming steeper and may approach a vertical tangent.
If the original derivative actually becomes zero, the inverse derivative is undefined, and no reciprocal relationship applies at that point.
Yes. If the slope of the original function is only known approximately, the reciprocal provides an efficient estimate for the inverse derivative.
Useful steps include:
• Find the approximate slope from a graph or table.
• Take the reciprocal to estimate the inverse slope.
• Evaluate how sensitive the reciprocal is to small errors in the original slope.
This works well unless the original slope is very close to zero.
Tables often list input values, output values, and slopes for the original function. To use them for an inverse derivative, you must locate the correct pair of corresponding values.
A corresponding point swaps the roles of input and output, allowing you to identify where the slope of the inverse is needed.
Once the output value in the table matches the input of the inverse, the reciprocal of the listed slope gives the inverse derivative.
Practice Questions
Question 1 (1–3 marks)
A function f is differentiable and strictly increasing. At x = 4, f(4) = 10 and f′(4) = 5.
Find the value of the derivative of the inverse function, (f⁻¹)'(10).
Question 1 (1–3 marks)
• Correct use of the reciprocal derivative relationship:
(f⁻¹)'(f(x)) = 1 / f′(x). (1 mark)
• Substitution of x = 4 and f′(4) = 5. (1 mark)
• Final answer: (f⁻¹)'(10) = 1/5. (1 mark)
Question 2 (4–6 marks)
The function g is one-to-one and differentiable, and a table of values gives:
g(2) = 7, g(5) = 12,
g′(2) = 4, g′(5) = 2.
(a) Explain why g has an inverse function.
(b) State the coordinates of the point on the graph of g⁻¹ corresponding to the point (2, 7) on the graph of g.
(c) Find (g⁻¹)'(7).
(d) Use your results to comment on the relative steepness of g and g⁻¹ at the corresponding points.
Question 2 (4–6 marks)
(a) • Statement that g is one-to-one (strictly monotonic) so it has an inverse. (1 mark)
(b) • Correct coordinate reversal: the corresponding point on g⁻¹ is (7, 2). (1 mark)
(c) • Correct use of derivative relationship:
(g⁻¹)'(g(x)) = 1 / g′(x). (1 mark)
• Substitution of x = 2 and g′(2) = 4. (1 mark)
• Final answer: (g⁻¹)'(7) = 1/4. (1 mark)
(d) • Appropriate comparison: since g has slope 4 at x = 2, and g⁻¹ has slope 1/4 at the reflected point, g is much steeper there than its inverse. (1 mark)
Total: 6 marks

