Derivatives of arcsin and arccos (3.4.2) | AP Calculus AB Notes

AP Syllabus focus:
‘Use the chain rule and inverse function relationships to derive and apply derivative formulas for arcsin x and arccos x and for compositions involving these functions.’

Understanding how to differentiate arcsin and arccos is essential because these inverse trigonometric functions appear frequently in calculus, especially when analyzing compositions requiring careful application of the chain rule.

Derivatives of arcsin and arccos

The derivatives of arcsin and arccos arise from the inverse relationship between trigonometric functions and their inverses, combined with strategic use of the chain rule, which states that the derivative of a composition depends on both the outer and inner functions. These derivative formulas allow quick differentiation of expressions involving inverse trigonometric functions, including those where the inside function is more complicated than a simple variable.

Foundations of Inverse Trigonometric Differentiation

To differentiate inverse trigonometric functions, it is crucial to recall that arcsin and arccos reverse the actions of sine and cosine on restricted domains, ensuring each inverse is a proper function.

Inverse function refers to a function that reverses another function’s input–output pairing.

Inverse Function: A function $f^{-1}$ satisfying $f(f^{-1}(x)) = x$ for all $x$ in its domain.

Inverse trigonometric functions specifically undo trigonometric functions on restricted intervals that guarantee one-to-one behavior. Because the trig functions are not one-to-one on their natural domains, restrictions ensure that each output corresponds to exactly one input.

The derivative formulas for arcsin and arccos come from differentiating the identities $y=\arcsin(x)$ and $y=\arccos(x)$ by rewriting them as $\sin(y)=x$ or $\cos(y)=x$ and then applying implicit differentiation.

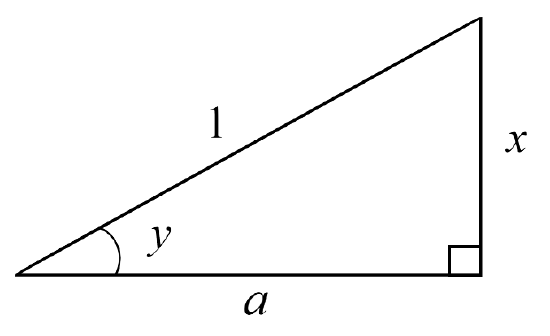
Right triangle representation for $y=\arcsin(x)$ , where $\sin y = x/1$ , so the opposite side has length $x$ and the hypotenuse has length $1$ . The adjacent side is $a=\sqrt{1-x^{2}}$ , leading to $\cos y = \sqrt{1-x^{2}}$ . This illustrates how the geometric relationship supports the inverse trigonometric derivative formula. Source.

Derivative Formula for arcsin

The derivative of $y=\arcsin(x)$ involves differentiating $\sin(y)=x$ implicitly and using the chain rule to treat $y$ as a function of $x$ .

$\frac{d}{dx}(\arcsin x) = \frac{1}{\sqrt{1 - x^{2}}}$
$x$ = input of the arcsin function, dimensionless

This formula is essential because it shows how the derivative increases as $x$ approaches $1$ or $-1$ , reflecting the steepness of the arcsin graph near its endpoints. It also highlights the relationship between inverse trig functions and algebraic expressions involving square roots.

After working with the arcsin derivative, notice how the square root in the denominator ensures the derivative is defined only on $[-1,1]$ , consistent with the domain of arcsin.

Derivative Formula for arccos

The derivative of $y=\arccos(x)$ emerges from differentiating $\cos(y)=x$ implicitly. Although a similar process is used as with arcsin, the derivative includes a negative sign due to the negative derivative of cosine.

$\frac{d}{dx}(\arccos x) = -\frac{1}{\sqrt{1 - x^{2}}}$
$x$ = input of the arccos function, dimensionless

The negative sign signals that arccos is a decreasing function on its domain, contrasting with arcsin, which is increasing.

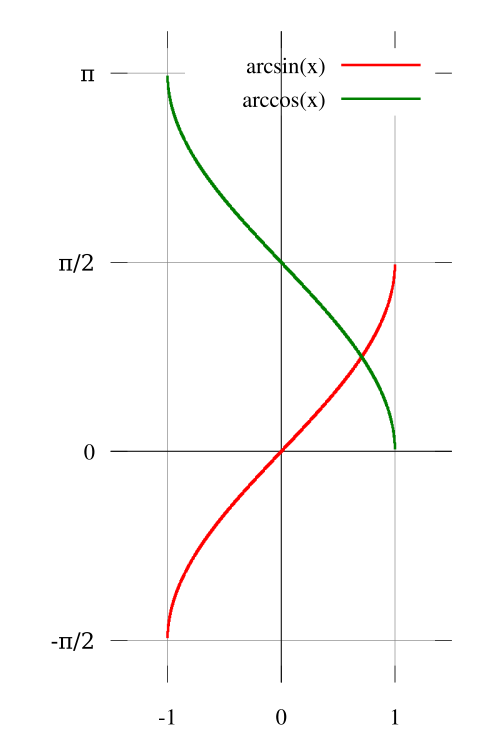
Graphs of $y=\arcsin(x)$ and $y=\arccos(x)$ on the interval $-1 \le x \le 1$ . The arcsine curve rises from $-\pi/2$ to $\pi/2$ , while the arccosine curve decreases from $\pi$ to $0$ . This highlights their shared domain and contrasting monotonic behavior. Source.

Between these two inverse trigonometric functions, the only difference in their derivative formulas is the sign. This pattern reflects the symmetry of their graphs and the relationship $\arccos(x) = \frac{\pi}{2} - \arcsin(x)$ .

Importance of the Chain Rule in Inverse Trig Differentiation

When differentiating inverse trig functions that involve more complicated inner expressions, the chain rule must be applied. The chain rule states that to differentiate a composite function, you multiply the derivative of the outer function by the derivative of the inner function.

Chain Rule: A rule stating that for a composite function $f(g(x))$ , the derivative is $f'(g(x)) \cdot g'(x)$ .

The chain rule ensures derivatives of expressions such as $\arcsin(2x)$ or $\arccos(g(x))$ incorporate both the inverse trig derivative and the derivative of the inside function.

Before applying these formulas, always identify:
• The outer function (arcsin or arccos).
• The inner function (the expression inside the parentheses).
• The derivative of the inner function.
• How the chain rule multiplies these components.

Structural Features of arcsin and arccos Derivatives

These inverse trigonometric derivatives share several key structural features:
• Both involve a denominator containing $\sqrt{1 - x^{2}}$ , tying them directly to the Pythagorean identity.
• Both only apply on domains where the square root is defined, aligning naturally with the domain restrictions of arcsin and arccos.
• Both derivatives become unbounded as $x$ approaches $\pm1$ , signaling vertical tangent behavior in their graphs.
• The sign difference between the formulas reflects the increasing nature of arcsin and the decreasing nature of arccos.

Applying Derivative Formulas in Compositions

When arcsin and arccos appear inside more complex expressions, use the following checklist:
• Identify the outer inverse trig function.
• Compute its derivative using the appropriate formula.
• Multiply by the derivative of the inside expression.
• Maintain careful notation to avoid sign errors, especially with arccos.
• Confirm that the expression remains within the domain of the inverse trig function.

These derivative formulas, coupled with clear chain rule application, allow efficient differentiation of inverse trigonometric expressions in a wide range of AP Calculus AB contexts.

FAQ

These square roots arise from applying the Pythagorean identity when rewriting a right triangle associated with the inverse trig expression.

When differentiating arcsin and arccos implicitly, the cosine or sine of an angle must be expressed using the triangle sides, which introduces the term sqrt(1 − x²).

This geometric origin explains why the derivative becomes undefined at the endpoints of the domain, where the square root becomes zero.

The chain rule is required whenever arcsin or arccos contains anything more complicated than a single variable, such as arcsin(2x − 5) or arccos(g(x)).

Identify the outer inverse trig function first, then check if the input expression is itself a function of x.

You will need to differentiate both layers.

Arccos is a decreasing function on its entire domain, so its slope must always be negative.

This comes from its inverse relationship with cosine, which decreases over the restricted interval used to define arccos.

Arcsin increases over its restricted interval, so its derivative is positive.

Typical errors include:
• Forgetting to multiply by the derivative of the inner function.
• Using the wrong sign for arccos derivatives.
• Applying the derivative rules outside the valid domain interval.

Checking the function structure before differentiating helps avoid most of these mistakes.

The vertical steepening of arcsin and arccos graphs near x = ±1 matches the derivative becoming unbounded there.

These formulas indicate where the graph has vertical tangents and how quickly the function changes in the central part of its domain.

Understanding this behaviour helps with sketching, estimating slopes, and reasoning about function behaviour without full calculations.

Practice Questions

Question 1 (1–3 marks)
Differentiate the function f(x) = arcsin(3x). State the domain restriction under which your derivative is valid.

Question 1 (3 marks total)

• Correct use of the chain rule for arcsin, giving f’(x) = 3 / sqrt(1 − 9x^2). (2 marks)
• Correct statement of the domain restriction: 1 − 9x^2 must be non-negative, or |3x| ≤ 1, so |x| ≤ 1/3. (1 mark)

Question 2 (4–6 marks)
Let h(x) = arccos(x^2 − 1).
(a) Find h’(x).
(b) The curve y = h(x) has a point at x = 1. Determine the slope of the tangent at this point.
(c) Explain why the value of the derivative at x = 1 is consistent with the behaviour of the arccos function.

Question 2 (6 marks total)

(a)
• Correct application of the chain rule to arccos: h’(x) = −1 / sqrt(1 − (x^2 − 1)^2) multiplied by derivative of the inside function 2x. (2 marks)
• Fully simplified derivative: h’(x) = −2x / sqrt(1 − (x^2 − 1)^2). (1 mark)

(b)
• Substitution of x = 1 into h’(x). (1 mark)
• Correct evaluation: h’(1) = −2 / sqrt(1 − 0) = −2. (1 mark)

Try All Topic Practice Questions

Written by:

Dr Rahil Sachak-Patwa

Oxford University - PhD Mathematics

Rahil spent ten years working as private tutor, teaching students for GCSEs, A-Levels, and university admissions. During his PhD he published papers on modelling infectious disease epidemics and was a tutor to undergraduate and masters students for mathematics courses.