Derivatives of arctan and Other Inverse Trig Functions (3.4.3) | AP Calculus AB Notes

AP Syllabus focus:
‘Find derivatives of arctan x and related inverse trigonometric functions, recognizing when these derivative formulas are useful in calculus problems.’

Understanding derivatives of arctangent and other inverse trigonometric functions is essential for analyzing composite functions, simplifying implicit relationships, and recognizing situations where inverse trig derivatives naturally appear in calculus.

The inverse trigonometric functions most relevant here are arctan, arccot, arcsec, and arccsc, each providing a way to recover an angle from a trigonometric ratio. Because these functions reverse trigonometric relationships, their derivatives have distinctive algebraic structures useful in both pure and applied calculus. Students must be able to recognize when inverse trig derivatives simplify expressions and distinguish these derivatives from those of ordinary trigonometric and logarithmic functions.

The Derivative of arctan x

The function arctan x returns the angle whose tangent equals $x$ .

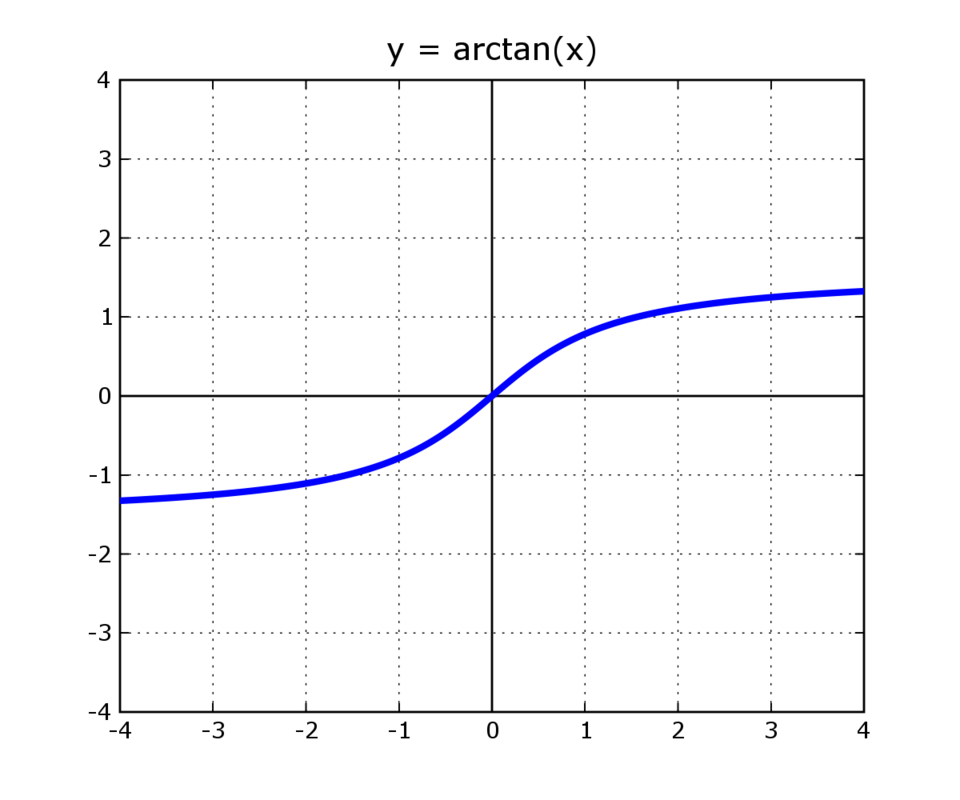
Graph of $y=\arctan x$ showing its S-shaped curve approaching horizontal asymptotes at $y=\pi/2$ and $y=-\pi/2$ . The curve illustrates that $\arctan x$ increases most rapidly near $x=0$ and flattens for large $|x|$ . This reflects the behavior of its derivative $1/(1+x^2)$ , which diminishes as $|x|$ grows. Source.

Inverse Trigonometric Function (arctan): The function that outputs the unique angle $\theta$ in $(-\frac{\pi}{2}, \frac{\pi}{2})$ such that $\tan(\theta)=x$ .

The derivative formula captures how quickly the output angle changes with respect to its input. Because the tangent function approaches vertical asymptotes at odd multiples of $\frac{\pi}{2}$ , the derivative of arctan includes a denominator that prevents undefined behavior on its domain.

$\frac{d}{dx}(\arctan x) = \frac{1}{1 + x^{2}}$
$x$ = Real input value

The structure of this derivative makes arctan a natural tool for situations involving rational expressions or slopes that approach zero as inputs grow large.

Derivatives of Other Inverse Trigonometric Functions

Although arctan x is the most commonly applied inverse trigonometric function in AP Calculus AB, students should also be familiar with derivatives of arccot x, arcsec x, and arccsc x, since they appear in differentiation tasks, implicit equations, and composite-function settings. These formulas arise from applying the chain rule to the identity defining each inverse function.

Inverse Trigonometric Function (arccot): The function that outputs the angle $\theta$ in $(0,\pi)$ such that $\cot(\theta)=x$ .

The derivative of arccot mirrors the form of the derivative of arctan but with a negative sign, reflecting the decreasing nature of the cotangent relationship.

$\frac{d}{dx}(\arccot x) = -\frac{1}{1 + x^{2}}$
$x$ = Real input value

Inverse secant and inverse cosecant introduce expressions involving absolute value because their underlying trigonometric functions are not one-to-one without domain restrictions.

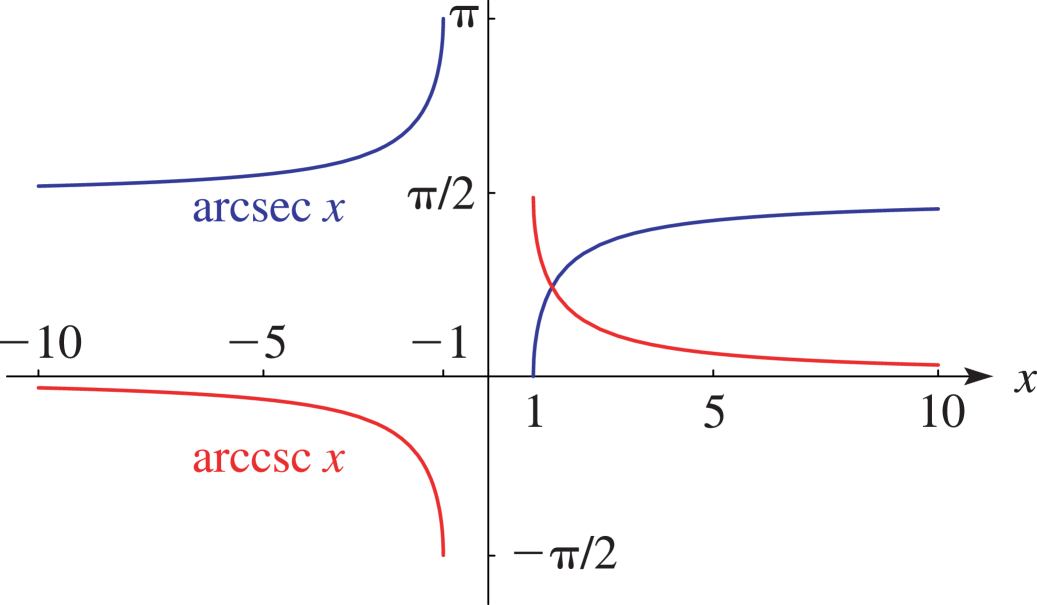
Graphs of $y=\operatorname{arcsec}x$ (blue) and $y=\operatorname{arccsc}x$ (red), defined only for $|x|>1$ . The figure emphasizes the restricted domains that motivate the absolute value terms in their derivatives, such as $1/(|x|\sqrt{x^2-1})$ . The note about complex values for $-1<x<1$ includes extra content beyond the AP syllabus but does not affect interpretation at this level. Source.

These restrictions ensure each inverse function is properly defined and differentiable where appropriate.

Inverse Trigonometric Function (arcsec): The function that outputs the angle $\theta$ in $[0,\pi]$ , $\theta \neq \frac{\pi}{2}$ , such that $\sec(\theta)=x$ .

A sentence must occur before the next equation block. The derivative of arcsec includes the absolute value of $x$ to ensure the expression remains valid and consistent with the restricted domain.

$\frac{d}{dx}(\arcsec x) = \frac{1}{|x|\sqrt{x^{2}-1}}$
$x$ = Real input value with $|x| \ge 1$

Similarly, the derivative of arccsc x follows from differentiating its implicit identity while honoring its domain constraints.

$\frac{d}{dx}(\arccsc x) = -\frac{1}{|x|\sqrt{x^{2}-1}}$
$x$ = Real input value with $|x| \ge 1$

These derivatives appear when differentiating expressions involving reciprocal trigonometric relationships or when solving problems that connect geometry with algebraic structure.

When These Derivative Formulas Are Useful

Recognizing when to apply inverse trigonometric derivatives is essential for efficient differentiation. Students should be attentive to structural cues indicating that an expression might simplify using these formulas. Key situations include:

Expressions involving rational forms resembling $\frac{1}{1+x^{2}}$ , which suggest a connection to the derivative of arctan $x$ .
Implicit relationships where tangent, cotangent, secant, or cosecant appear in an equation linking variables.
Composite structures such as $\arctan(g(x))$ or $\arcsec(f(x))$ , which require applying the chain rule in addition to the inverse trig derivative formula.
Modeling or geometry contexts where slopes or angles arise naturally from ratios that correspond to trigonometric definitions.
Functions with domain restrictions where absolute value expressions in the derivative ensure correct and consistent interpretations.

Applying Derivative Rules to Composites

Inverse trigonometric functions often appear nested within more complex expressions. The chain rule plays a central role in ensuring accurate differentiation. When differentiating a composite involving an inverse trig function:

Identify the outer function (the inverse trig expression).
Determine the inner function and find its derivative.
Multiply the derivative of the outer function by the derivative of the inner function to complete the chain rule.
Ensure all domain and absolute-value restrictions are respected to maintain correctness.

These strategies allow students to analyze complicated relationships and confidently compute derivatives using the structure and properties of inverse trigonometric functions.

FAQ

The derivative of arctan has the simplest algebraic structure because its domain is all real numbers, so no absolute values or domain-based restrictions appear.

In contrast, functions like arcsec or arccsc require restricted domains for their inverses to be valid. These restrictions lead to derivative formulas involving absolute values and square roots, reflecting changes in behaviour near points where the original trigonometric functions are not one-to-one.

Absolute values appear when the inverse function is defined on domains where the input can be positive or negative but the derivative relies on a quantity that must stay non-negative.

For arcsec and arccsc, the original trig functions involve ratios whose magnitudes matter more than their signs. The absolute value ensures the derivative remains valid across the allowed intervals.

Look for algebraic patterns such as:
• A rational expression resembling 1 divided by a quadratic, which often signals arctan or arccot.
• A square root in the denominator combined with an absolute value, suggestive of arcsec or arccsc.

These patterns help reverse-engineer the original function, particularly when differentiating composite or implicit expressions.

Yes. Because functions like arctan flatten out as x becomes large, their derivatives help examine rates of change approaching infinity.

Inverse trig derivatives can also convert complicated ratios into manageable forms when assessing whether a function is continuous or differentiable at a point. Their predictable behaviour near boundaries makes them useful for analysing limiting behaviour.

Implicit equations often involve variables appearing in trigonometric ratios not easily solved for a single variable. Applying an inverse trig function can isolate an angle or ratio that captures the relationship more cleanly.

When differentiating, the resulting expressions naturally involve derivatives of arctan, arcsec, or similar functions, allowing the process to proceed without explicitly rearranging the original equation.

Practice Questions

Question 1 (1–3 marks)
Differentiate the function h(x) = arctan(3x).
Give your answer in its simplest form.

Question 1 (1–3 marks total)
• 1 mark for identifying the use of the chain rule.
• 1 mark for correctly differentiating arctan(u) to give 1/(1 + u^2).
• 1 mark for multiplying by the derivative of the inner function 3x, resulting in 3/(1 + 9x^2).

Question 2 (4–6 marks)
A function satisfies y = arcsec(2x + 1).
(a) Find dy/dx.
(b) The point P on the curve has x = 2. Determine the exact value of dy/dx at point P, stating any domain conditions that justify your working.

Question 2 (4–6 marks total)

(a)
• 1 mark for recognising the derivative of arcsec(u) as 1/(|u| sqrt(u^2 − 1)).
• 1 mark for correct substitution u = 2x + 1.
• 1 mark for applying the chain rule and multiplying by the derivative of the inner expression (which is 2).

(b)
• 1 mark for substituting x = 2 into the derived expression for dy/dx.
• 1 mark for correctly evaluating the expression to obtain the exact numerical value.
• 1 mark for stating the domain condition |2x + 1| ≥ 1 and confirming that x = 2 satisfies it.

Try All Topic Practice Questions

Written by:

Dr Rahil Sachak-Patwa

Oxford University - PhD Mathematics

Rahil spent ten years working as private tutor, teaching students for GCSEs, A-Levels, and university admissions. During his PhD he published papers on modelling infectious disease epidemics and was a tutor to undergraduate and masters students for mathematics courses.

Oxford University - PhD Mathematics

AP Calculus AB study notes

3.4.3 Derivatives of arctan and Other Inverse Trig Functions

The Derivative of arctan x

Derivatives of Other Inverse Trigonometric Functions

When These Derivative Formulas Are Useful

Applying Derivative Rules to Composites

FAQ

Practice Questions

Hire a tutor

AP Calculus AB study notes

3.4.3 Derivatives of arctan and Other Inverse Trig Functions

Derivatives of arctan and Related Inverse Trigonometric Functions

The Derivative of arctan x

Derivatives of Other Inverse Trigonometric Functions

When These Derivative Formulas Are Useful

Applying Derivative Rules to Composites

FAQ

Practice Questions

Hire a tutor