Inverse Trig Functions and Principal Values (3.4.1) | AP Calculus AB Notes

AP Syllabus focus:
‘Review definitions, domains, and ranges of arcsin, arccos, and arctan so their inverses are functions, preparing to use derivative formulas for inverse trig functions.’

Inverse trigonometric functions provide the essential bridge from trigonometric relationships back to their corresponding angle measures, and understanding their principal values ensures these inverses behave as proper functions.

Principal Values and the Need for Restrictions

Inverse trigonometric functions must be defined carefully because the original trigonometric functions are not one-to-one on their natural domains. A function must be one-to-one to possess an inverse, so mathematicians restrict the domains of sine, cosine, and tangent to intervals where they do not repeat values.

Principal Value: The unique output of an inverse trigonometric function obtained by restricting the domain of the original trig function so that the inverse becomes a real-valued function.

These restrictions guarantee that each inverse trig function returns a single, predictable angle, making them suitable for calculus operations such as differentiation.

arcsin and Its Principal Value Range

The inverse sine function, arcsin, undoes the action of the sine function on a restricted interval where sine is one-to-one.

arcsin: The inverse of sine defined so that $y = \arcsin(x)$ is the angle $y$ in the interval $[-\frac{\pi}{2}, \frac{\pi}{2}]$ whose sine is $x$ .

This interval is chosen because sine increases monotonically from $-\frac{\pi}{2}$ to $\frac{\pi}{2}$ and covers the full range $[-1,1]$ . Therefore:
• Domain of arcsin: $[-1,1]$
• Range of arcsin: $[-\frac{\pi}{2}, \frac{\pi}{2}]$

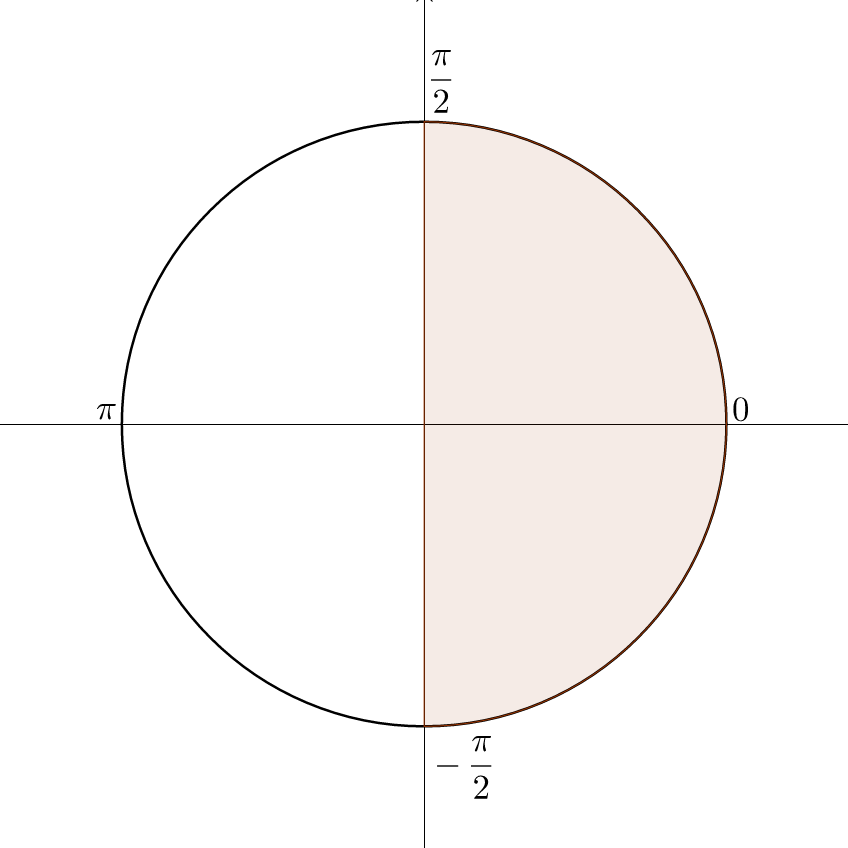
Shaded region on the unit circle showing the principal values of $y = \arcsin(x)$ from $-\frac{\pi}{2}$ to $\frac{\pi}{2}$ on the right half of the circle. The highlighted domain emphasizes why inverse sine outputs only these angles. This figure visually supports the definition of principal values for $\arcsin$ . Source.

When differentiating composite expressions containing arcsin, it is crucial to keep these principal values in mind, since they determine the behavior of the function and ensure correct interpretation of derivative signs.

arccos and Its Principal Value Range

The inverse cosine function, arccos, requires a different restricted interval from arcsin because cosine decreases on a different part of the unit circle.

arccos: The inverse of cosine defined so that $y = \arccos(x)$ is the angle $y$ in the interval $[0, \pi]$ whose cosine is $x$ .

Cosine is one-to-one and strictly decreasing on $[0,\pi]$ , making this interval ideal for defining arccos consistently.

Important properties include:
• Domain of arccos: $[-1,1]$
• Range of arccos: $[0,\pi]$

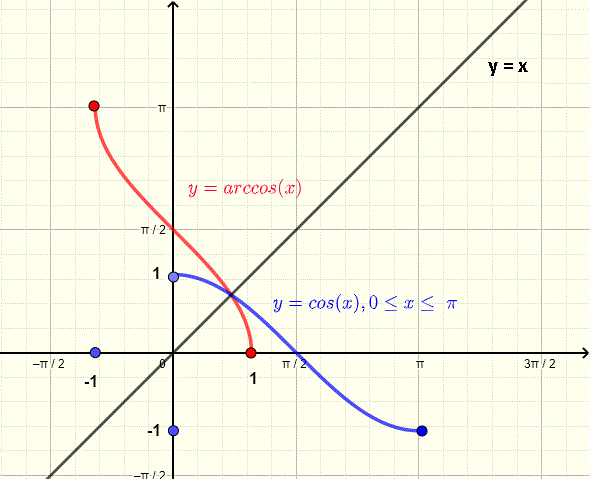
Graph of $y = \cos(x)$ restricted to $0 \le x \le \pi$ and its inverse $y = \arccos(x)$ reflected across $y = x$ . The diagram highlights the required domain restriction that ensures cosine becomes one-to-one. The resulting inverse curve clearly shows why $\arccos(x)$ takes values only in $[0,\pi]$ . Source.

These values play a key role when applying derivative formulas, which rely on the specified range to avoid ambiguity when selecting angle outputs.

arctan and Its Principal Value Range

The tangent function repeats every $\pi$ units, so its inverse, arctan, is defined on a centered interval capturing its monotonic behavior.

arctan: The inverse of tangent defined so that $y = \arctan(x)$ is the angle $y$ in the interval $(-\frac{\pi}{2}, \frac{\pi}{2})$ whose tangent is $x$ .

This interval excludes the vertical asymptotes of tangent and produces a smooth, continuous inverse function.

Key characteristics:
• Domain of arctan: all real numbers
• Range of arctan: $(-\frac{\pi}{2}, \frac{\pi}{2})$

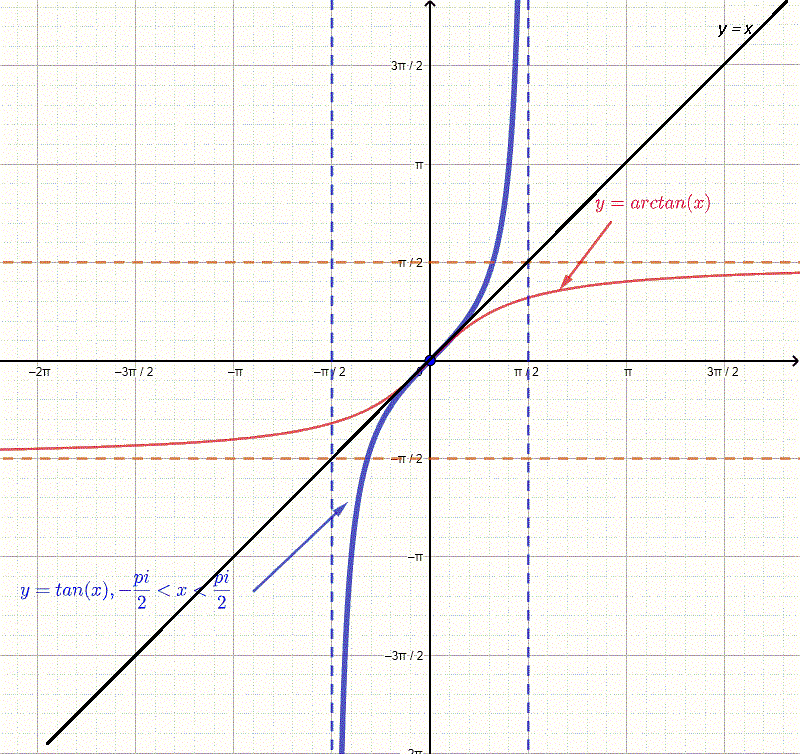
Graph of $y = \arctan(x)$ along with the restricted tangent curve and horizontal asymptotes at $y = -\frac{\pi}{2}$ and $y = \frac{\pi}{2}$ . The S-curve shows the full real domain and bounded range of the inverse tangent function. Extra details such as asymptotes exceed syllabus requirements but help illustrate how the principal range arises. Source.

Understanding this range is crucial when interpreting the increasing behavior of arctan and anticipating the sign of its derivative in differentiation contexts.

How Principal Values Support Differentiation

The AP Calculus AB syllabus requires familiarity with the definitions, domains, and ranges of arcsin, arccos, and arctan specifically to prepare students for applying derivative formulas. These formulas depend on the functions being well-defined and single-valued. For instance, the derivative of an inverse trig function reflects how an angle changes relative to a change in its trigonometric ratio. Without principal values, inverse trig expressions could yield multiple possible angles, making derivatives meaningless.

To support successful differentiation, students should remember the following structural ideas:

Why Domain Restrictions Matter

• They ensure each inverse trig function is a true function with exactly one output for each input.
• They determine the correct sign of derivative expressions because each range corresponds to a specific quadrant.
• They allow differentiation rules involving arcsin, arccos, and arctan to rely on predictable angle behavior.

How Principal Values Inform Calculus Procedures

• When differentiating compositions involving inverse trig functions, recognizing the appropriate range prevents misinterpretation of angle values.
• Many derivative formulas of inverse trig functions involve radicals, and knowing the ranges helps determine whether the radicand or the resulting derivative is positive or negative.
• Understanding the monotonic intervals of sine, cosine, and tangent clarifies why chain rule applications remain consistent across the inverse trig family.

These structural insights align with the syllabus emphasis on preparing for derivative formulas by developing a strong conceptual foundation in inverse trigonometric definitions and ranges.

FAQ

Each trigonometric function becomes one-to-one on a different interval, so the chosen principal value range must match the portion of the unit circle where the function is strictly increasing or strictly decreasing.

Sine behaves monotonically on the right-hand vertical interval, cosine on the upper semicircle, and tangent between its two vertical asymptotes. These differences ensure each inverse returns a unique angle.

A helpful approach is to examine graphs of sine, cosine, and tangent restricted to their monotonic intervals. Each graph forms a smooth, non-repeating curve that can be “flipped” across the line y = x to create its inverse.

This method highlights the link between the shape of the original function and the allowable angle outputs of its inverse.

Both depend on the ratio opposite over hypotenuse in right-triangle contexts, so their input values must lie between -1 and 1. However, their outputs correspond to angles in different parts of the unit circle.

Arcsin selects angles on the right-hand side, while arccos selects angles on the upper semicircle. These ranges avoid overlap and ensure each function is single-valued.

The expression is undefined because no real angle produces such a trigonometric value. For instance, no real angle has sine greater than 1 or less than -1.

In applied settings, this usually indicates an error in modelling, a miscalculation, or the need for complex-number methods not used in AP Calculus AB.

Tangent grows without bound as it approaches its vertical asymptotes, and when this behaviour is inverted, the resulting arctan graph approaches horizontal asymptotes.

This creates an S-shaped curve with a smooth transition from negative to positive output values. It visually reflects how arctan accepts all real inputs but restricts outputs to a finite interval.

Practice Questions

Question 1 (1–3 marks)
The function f is defined by f(x) = arcsin(x).
(a) State the domain of f. (1 mark)
(b) State the range of f. (1 mark)
(c) Explain why the sine function must be restricted in order for arcsin to be defined as a function. (1 mark)

Question 1
(a) Domain of f: the interval from -1 to 1 inclusive.
• 1 mark for stating the correct domain.

(b) Range of f: the interval from -pi/2 to pi/2 inclusive.
• 1 mark for stating the correct range.

(c) Sine is not one-to-one over its full domain, so without restriction it would not have a unique inverse value for each output.
• 1 mark for correctly stating that sine must be restricted because it is not one-to-one on its natural domain.
• Equivalent explanations earn full credit.

Question 2 (4–6 marks)
Let g be the inverse of the tangent function restricted to its principal domain.
(a) State the domain and range of g. (2 marks)
(b) Using the graph of tangent on its restricted interval, explain why g is one-to-one and hence invertible. (2 marks)
(c) A student claims that arctan(x) can output values equal to pi/2 or negative pi/2. Determine whether this is correct and justify your answer. (1–2 marks)

Question 2
(a) Domain of g: all real numbers.
Range of g: the interval from -pi/2 to pi/2.
• 1 mark for correctly stating the domain.
• 1 mark for correctly stating the range.

(b) On the restricted interval, tangent increases strictly and does not repeat any output value, so it is one-to-one. Therefore it has a well-defined inverse.
• 1 mark for noting the strict increase or monotonic behaviour of tangent on the interval.
• 1 mark for identifying that this ensures invertibility.

(c) The student’s claim is incorrect because arctan(x) approaches pi/2 and -pi/2 asymptotically but never attains these values.
• 1 mark for stating the claim is incorrect.
• 1 mark for providing a correct justification involving limiting behaviour or asymptotes.

Try All Topic Practice Questions

Written by:

Dr Rahil Sachak-Patwa

Oxford University - PhD Mathematics

Rahil spent ten years working as private tutor, teaching students for GCSEs, A-Levels, and university admissions. During his PhD he published papers on modelling infectious disease epidemics and was a tutor to undergraduate and masters students for mathematics courses.