AP Syllabus focus:
‘Practice deciding whether to use power, product, quotient, chain, or implicit differentiation based on the structure of a given expression before computing a derivative.’
Choosing the correct differentiation rule begins with recognizing a function’s structure. Effective selection streamlines computation, avoids unnecessary algebra, and ensures accurate derivatives across polynomial, rational, composite, and implicitly defined expressions.
Understanding the Purpose of Rule Selection
Before differentiating, students must examine how a function is built. A function’s algebraic structure determines whether the power rule, product rule, quotient rule, chain rule, or implicit differentiation is the most appropriate tool. Selecting the correct rule reduces errors and leads to more efficient problem solving in AP Calculus AB.
Identifying Structural Features in Functions
A careful reading of the expression’s components helps determine which rule matches the situation. To guide this process, focus on recognizing the relationships among multiplied, divided, or nested functions.
Observable Features That Guide Rule Selection
Single-term power expressions typically indicate the power rule.
Products of two or more variable-dependent factors signal the product rule.
Fractions with variable expressions in numerator and denominator require the quotient rule.
Nested functions, in which one function is inside another, demand the chain rule.
Equations where cannot be easily isolated often call for implicit differentiation.
The Power Rule: When It Applies
The power rule is used when differentiating expressions of the form or constant multiples of such terms. It is efficient only when the expression is a single power function, not a product or composition.
Power Function: A function of the form , where is any real number.
Students should ensure the term is not actually part of a product or composite function before applying this rule.
Recognizing When to Use the Product Rule
The product rule is needed when two differentiable expressions are multiplied and both depend on the variable.
Product Rule: A rule stating that the derivative of is .
A sentence must follow a definition, so note that failing to identify a hidden product—such as a constant multiplied by a function versus two variable-dependent expressions—can lead to misuse of the power rule.
Indicators That Signal a Product
A multiplication dot or explicit parentheses
Two variable expressions adjacent without an operation symbol
A trigonometric or exponential function multiplied by a polynomial
When the Quotient Rule Is the Correct Choice
The quotient rule is used when an expression is a ratio of differentiable functions and neither the numerator nor denominator is a constant.
Quotient Rule: A rule for differentiating , requiring and producing .
It is important to avoid the temptation to split a quotient unless algebraic simplification is valid and advantageous.
Situations Suggesting the Quotient Rule
A variable expression sits entirely in the denominator
Both numerator and denominator require differentiation
Simplifying before differentiating would be complicated or impossible
Choosing the Chain Rule for Composite Functions
The chain rule is essential when one function is nested inside another. Recognizing a composite structure ensures that the derivative accounts for both the outer and inner functions.
Recognizing a composite structure ensures that the derivative accounts for both the outer and inner functions.
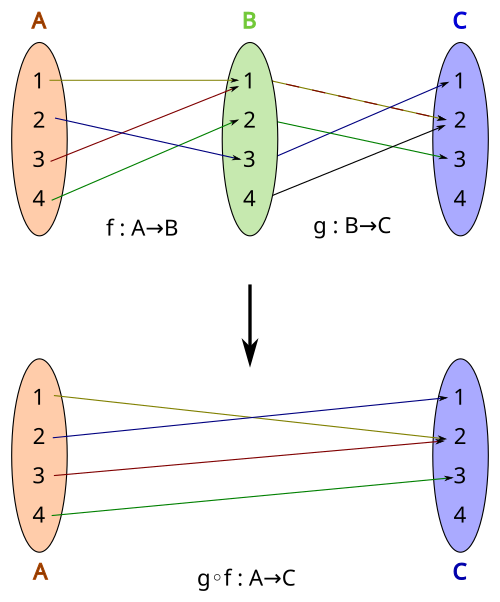
This diagram illustrates two functions, and , and their composition , showing how an input moves through inner and outer functions. It emphasizes the layered structure used when applying the chain rule. The set-based notation is more formal than required for AP Calculus AB but reinforces how composite mappings operate. Source.
Composite Function: A function formed by applying one function to the output of another, written as .
A sentence follows the definition to clarify that many expressions disguise their composite nature by combining polynomials with trigonometric, exponential, or logarithmic operations.
Structural Signs of a Composite
A function applied to an expression more complex than a single variable
Parentheses within trigonometric, exponential, or logarithmic functions
Powers applied to multi-term expressions
When Implicit Differentiation Is Necessary
Implicit differentiation becomes appropriate when the equation involves both and in a way that makes solving explicitly for difficult or impossible.
Implicit Equation: An equation in which the dependent variable cannot be isolated easily on one side.
After the definition, it is useful to note that students must treat as a function of , applying the chain rule to -terms when differentiating.
Clues That Implicit Differentiation Should Be Used
and appear intermixed in products, powers, or trigonometric functions
Rearranging to isolate would require extensive algebra
The relationship is given primarily to express a curve rather than a function
A Practical Strategy for Selecting the Correct Rule
To make efficient decisions, apply a systematic process:
Step-by-Step Identification
Scan the expression for multiplication, division, or nested structure.
Determine the main operation that connects the highest-level components of the function.
Check for combinations requiring multiple rules in sequence.
Simplify algebraically when appropriate, but only if simplification reduces—not increases—complexity.
Key Reminders
A function may require more than one rule, but the primary structure guides the first step.
Misidentifying the structure often leads to the wrong rule and incorrect differentiation.
Fluency develops through practice in recognizing patterns and anticipating which rules apply.
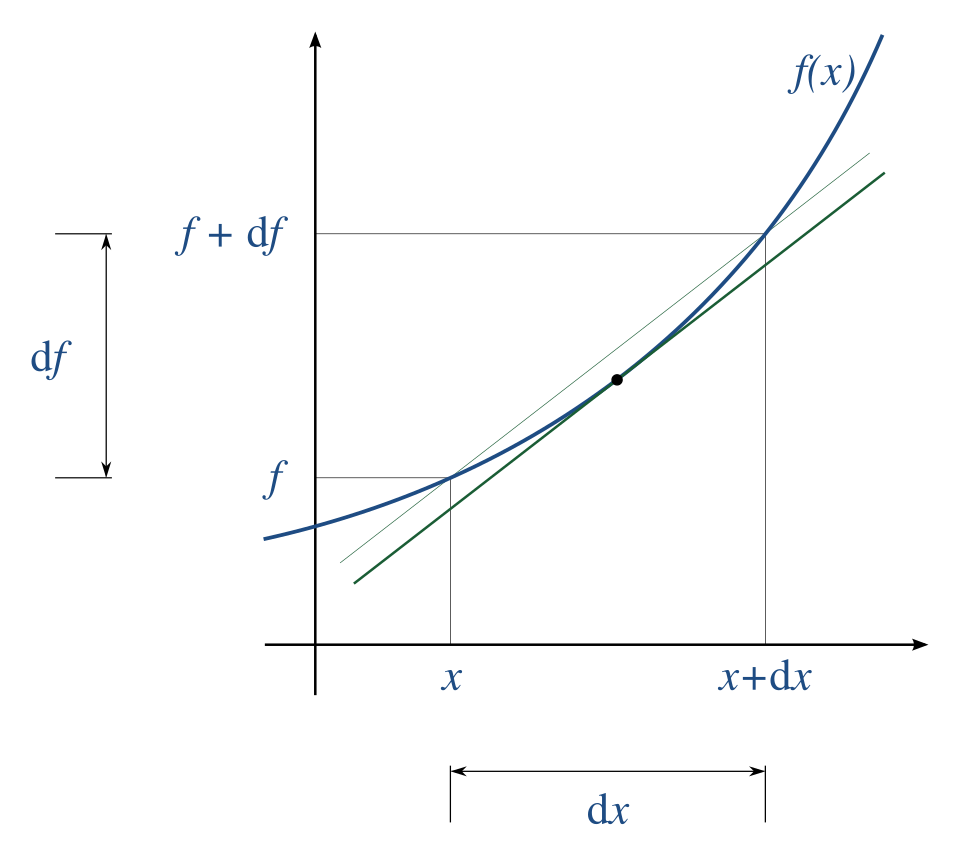
This graph shows a curve with a tangent line at a point, emphasizing that all differentiation rules ultimately compute the slope of the tangent. The geometric meaning connects rule selection to the purpose of finding instantaneous rate of change. The clean layout keeps the focus on the essential relationship between curve and tangent. Source.
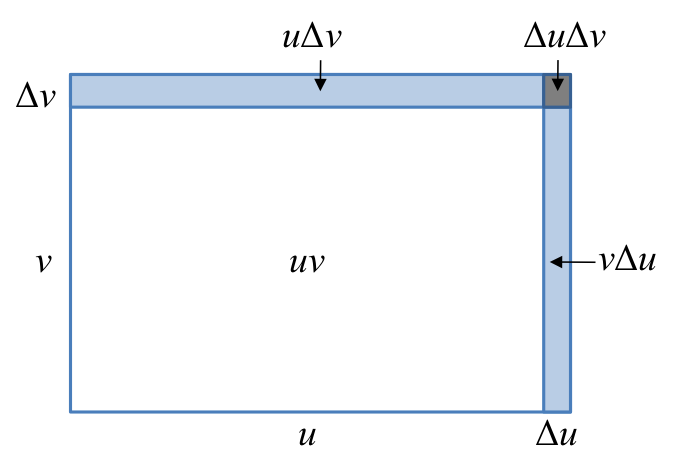
This diagram decomposes changes in the area of a rectangle whose side lengths vary, illustrating the structure behind . It visually reinforces when the product rule is needed. The geometric reasoning shown is more detailed than required in AP Calculus AB but strengthens intuition. Source.
FAQ
Look for the highest-level structure first: the operation that would be performed last if you evaluated the function.
• If multiplication combines two variable expressions, the product rule is usually primary.
• If division is the final operation, the quotient rule takes priority.
• If an outer function is applied to an inner expression, the chain rule will dominate.
Work from the outside inward rather than focusing on individual terms.
A frequent error is applying the power rule in situations where it does not apply, such as to products or quotients.
Another common mistake is failing to notice nested functions, especially when parentheses are subtle or a power is applied to a multi-term expression.
Carefully inspecting structure before differentiating helps avoid both mistakes.
Simplification is helpful if it clearly reduces complexity without altering the function’s structure.
Good times to simplify include:
• factoring out constants
• expanding simple brackets if it removes an unnecessary product
• rewriting a quotient as a product only when the denominator is a constant
Avoid simplification if it introduces a more complicated expression or disguises the rule actually required.
Check whether more than one structural feature is present. For example, a product involving composite functions will require both the product and chain rules.
A useful approach:
• Identify the dominant outer operation first.
• Then examine each component to see whether it is itself a product, quotient, or composite.
If a component requires a rule, you apply it inside the main rule.
Choosing the right rule immediately prevents unnecessary algebraic expansion or rearrangement, which saves valuable exam time.
It also reduces the risk of cascading errors. A wrong rule leads to incorrect structure in the derivative, making later steps harder to correct.
Efficient rule selection helps maintain accuracy while keeping work clear and manageable under exam conditions.
Practice Questions
A function is given by h(x) = (3x + 1)(x² − 4).
(a) State which differentiation rule should be used to differentiate h.
(b) Differentiate h.
Question 1 (1–3 marks)
(a) Correct identification of the product rule.
• 1 mark
(b) Correct differentiation using the product rule:
h’(x) = (3)(x² − 4) + (3x + 1)(2x)
• 1 mark for correct application of the rule
• 1 mark for a fully simplified or correct unsimplified derivative
(e.g. h’(x) = 3x² − 12 + 6x² + 2x, or 9x² + 2x − 12)
Total: 3 marks
Let f(x) = (2x − 5) / g(x), where g is a differentiable function with g(2) = 4 and g’(2) = −3.
(a) State the primary differentiation rule required to find f’(x).
(b) Find f’(x) in terms of g(x) and g’(x).
(c) Hence compute f’(2).
(d) Briefly explain why the rule used in part (a) is more appropriate than applying the power rule directly.
Question 2 (4–6 marks)
(a) Identification of the quotient rule.
• 1 mark
(b) Correct expression for f’(x) using the quotient rule:
f’(x) = [(2)(g(x)) − (2x − 5)(g’(x))] / [g(x)]²
• 1 mark for correct structure
• 1 mark for correct numerator
(c) Substitution of x = 2 into the derivative:
f’(2) = [(2)(4) − (2(2) − 5)(−3)] / (4)²
• 1 mark for correct substitution
• 1 mark for correct numerical evaluation
(Working gives f’(2) = (8 − (−3)) / 16 = 11/16)
(d) Correct explanation:
• 1 mark for noting that the expression is a quotient of two variable-dependent functions, so the power rule alone cannot be applied.
Total: 6 marks

