AP Syllabus focus:
‘Recognize when a single derivative requires a combination of rules, such as product and chain rules together, and plan an efficient order for applying them.’
Differentiating complex expressions often requires combining multiple derivative rules. Understanding how these rules interact helps students build efficient strategies for approaching multi-layered functions in calculus.
Combining Multiple Rules in One Problem
When differentiating a function involving several algebraic structures, trigonometric components, or nested compositions, AP Calculus AB students must identify which differentiation rules apply and in what order. This subsubtopic emphasizes recognizing structural cues in a function, selecting the appropriate rules, and organizing the differentiation process to avoid errors. Because complex expressions often mix multiplication, division, and composition, it is essential to determine whether the product rule, quotient rule, or chain rule (or a combination) is required before beginning any computation.
Recognizing Structural Features That Signal Multiple Rules
Correctly interpreting the structure of a function is central to applying multiple rules effectively. Students should learn to inspect functions for the presence of:
Products of functions, which signal the use of the product rule.
Ratios of functions, which signal the use of the quotient rule.
Nested functions, which signal the use of the chain rule.
Constants and linear factors, which may simplify a derivative when factored strategically.
Because the form of a function dictates the derivative rule, careful examination is the first step in any multistep differentiation task.
The Role of the Product Rule in Multistep Problems
The product rule arises when a function is expressed as the product of two differentiable functions.
Product Rule: If f(x)=u(x)v(x), then f′(x)=u′(x)v(x)+u(x)v′(x).
In multistep problems, the product rule rarely appears in isolation. One or both factors may themselves be composite, requiring application of the chain rule. For example, if one factor contains a trigonometric or exponential expression with a nontrivial inside function, the derivative of that factor requires differentiating the outside function first and then the inside function. Planning the sequence of differentiation helps prevent misapplication of rules and ensures each part of the product is handled accurately.
The Quotient Rule and Its Interaction with Compositions
Whenever a function is written as a ratio, the quotient rule becomes necessary.
Quotient Rule: If f(x)=u(x)/v(x), then f′(x)= (u′(x)v(x) − u(x)v′(x)) / (v(x))².
Unlike the product rule, the quotient rule includes subtraction and a squared denominator, making algebraic precision especially important. When either u(x) or v(x) contains a composite structure, the chain rule must be applied inside the quotient rule. Recognizing these layers allows a student to differentiate methodically rather than attempting to simplify prematurely, which may introduce unnecessary complexity.
The Chain Rule as the Unifying Technique
The chain rule appears in nearly every complex differentiation problem because many functions in calculus are compositions.
Chain Rule: If y=f(g(x)), then dy/dx = f′(g(x)) ⋅ g′(x).
Students must identify the outer function and inner function clearly before differentiating.
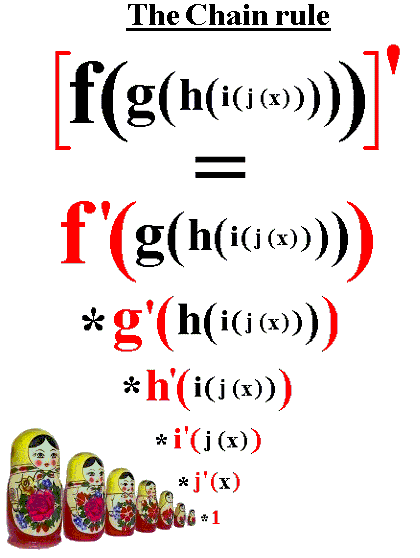
This diagram displays the chain rule in both function and Leibniz notation, highlighting how the derivative of a composite function depends on the outer and inner derivatives. It reinforces the form y = f(g(x)) and the relationship dy/dx = f′(g(x))·g′(x). The labels extend slightly beyond the syllabus wording but support conceptual understanding of composite structure. Source.
A sentence of explanation fits here to separate conceptual blocks and reinforce student understanding.
Planning the Order of Rule Application
A central skill described in this subsubtopic is determining an efficient order for applying derivative rules. This planning step should occur before any differentiation begins. Students should consider the following guidelines:
Determine whether the expression is fundamentally a product, quotient, or single composite.
Identify which components require the chain rule.
Differentiate from the outermost structure inward.
Avoid unnecessary algebraic manipulation before differentiating unless it simplifies the structure.
Keep track of each component using clear notation, especially when applying multiple rules sequentially.
By following these steps, students minimize mistakes and maintain clarity throughout longer derivatives.
Layered Use of Rules in Increasingly Complex Expressions
Many AP-level functions require several derivative rules in combination. Situations that require multiple rules include:
Products where each factor is a composite requiring the chain rule.
Quotients involving exponential or logarithmic expressions with inner functions.
Mixed algebraic-trigonometric compositions that require systematic peeling of layers.
Expressions where constants or powers distribute across products or compositions, altering which rule is most efficient.
Because multistep derivatives often involve nested rules, students benefit from practicing rule identification and consistent symbolic organization.
Maintaining Precision Through Notation and Interpretation
Throughout multistep differentiation, accurate notation plays a crucial role. Parentheses must be used consistently to preserve the intended grouping of functions. Terms such as inner function, outer function, numerator function, and denominator function help clarify each stage of the differentiation. When rules are combined, the meaning of each derivative must remain explicit, and students should maintain the structural logic of the original function throughout the process.
Strong conceptual understanding ensures that combining multiple derivative rules in one problem becomes an organized and predictable task rather than an exercise in memorization.
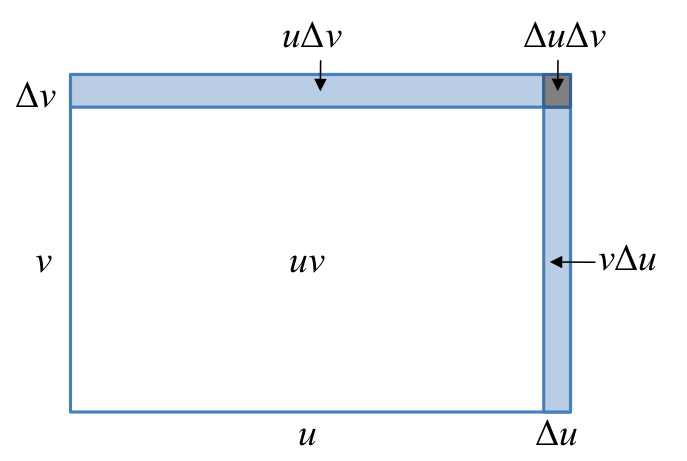
This diagram gives a geometric interpretation of the product rule by showing how changes in each factor contribute to the total change in a product. The labeled regions correspond to the two additive components u′(x)v(x) and u(x)v′(x). Although geometric, it remains aligned with calculus concepts relevant to understanding combined differentiation rules. Source.
FAQ
Simplification helps when it removes products, quotients, or unnecessary powers, but it is not always beneficial.
Factorising or expanding may reduce complexity, but it can also produce additional terms that require more work.
Good candidates for simplification include:
• Expressions where a common factor can be extracted.
• Quotients that can be rewritten as negative powers.
• Products that turn into single-term powers after algebraic manipulation.
Avoid simplifying when it obscures an inner function or hides a structure needed for the chain rule.
The most frequent error is forgetting to differentiate the inner function when applying the chain rule inside a product or quotient.
Other typical issues include:
• Dropping brackets, leading to incorrect sign distribution.
• Mixing up which part of the function is u and which is v in the product or quotient rule.
• Treating a function as a product when it is actually a composition, or vice versa.
Careful structural inspection before differentiating prevents most of these errors.
Many functions hide compositions inside apparently simple components.
Even factors that appear basic, such as sine, exponential, or logarithmic expressions, frequently contain an inner function that must be differentiated.
Examples of hidden compositions include:
• sin(ax + b)
• e^(g(x))
• (3x – 1)⁵
If any component contains its own function inside, the chain rule is active regardless of the outer structure.
Clear notation is essential.
Writing out each component explicitly helps track which rule applies at each stage.
A structured approach can include:
• Defining u and v before using the product or quotient rule.
• Label the inner and outer functions when using the chain rule.
• Using spacing and consistent brackets to separate terms.
• Writing intermediate derivatives rather than attempting mental shortcuts.
Good layout reduces algebraic errors and improves accuracy.
Begin by identifying the outermost operation. That operation determines the primary rule.
For example, if the function is a quotient, the quotient rule governs the overall differentiation, even if products or compositions lie inside.
A useful hierarchy is:
• Check for quotient structure first.
• If no quotient, check for product structure.
• If neither, examine whether the entire expression is a composition.
Once the outer rule is chosen, apply inner rules inwards, peeling the expression layer by layer.
Practice Questions
Question 1 (1–3 marks)
A function is defined by
f(x) = x² sin(3x).
(a) State which differentiation rules must be used to find f '(x).
(b) Find f '(x).
Question 1 (1–3 marks)
(a) 1 mark
• Correctly states that the product rule and chain rule are required.
(b) 2 marks
• 1 mark for correctly applying the product rule structure: derivative of x² times sin(3x) plus x² times derivative of sin(3x).
• 1 mark for correctly applying the chain rule to differentiate sin(3x) to obtain 3cos(3x).
Final answer: f '(x) = 2x sin(3x) + 3x² cos(3x).
Question 2 (4–6 marks)
A function is defined by
h(x) = (e^(2x) cos x) / (x² + 1).
(a) Identify all differentiation rules required to differentiate h(x).
(b) Show that
h '(x) = [e^(2x)(2cos x − sin x)(x² + 1) − 2x e^(2x) cos x] / (x² + 1)².
(c) Hence, or otherwise, determine the value of h '(0).
Question 2 (4–6 marks)
(a) 1 mark
• Identifies the quotient rule, product rule, and chain rule as necessary.
(b) 3 marks
• 1 mark for correct quotient rule structure applied to h(x).
• 1 mark for correctly differentiating the numerator using both product rule and chain rule.
• 1 mark for arriving at the given expression or an algebraically equivalent form.
(c) 1–2 marks
• 1 mark for correct substitution of x = 0 into the expression for h '(x).
• 1 mark for obtaining the correct value: h '(0) = 1.

