Using Graphs, Tables, and Technology (3.5.3) | AP Calculus AB Notes

AP Syllabus focus:
‘Use graphs, tables, and technology to check derivatives and to help select appropriate differentiation procedures for complicated or unfamiliar functions.’

Graphs, tables, and technology offer essential insight when derivatives are difficult to compute directly, allowing students to verify behavior, identify patterns, and choose suitable differentiation strategies.

Using Visual and Numerical Tools to Guide Differentiation

Students often face expressions where the correct differentiation rule is not immediately obvious. Graphs, tables, and technology-based outputs help reveal functional structure, rates of change, and smoothness, all of which influence the choice of derivative techniques. These tools do not replace analytical methods; instead, they support decision-making and verification, especially for complicated or unfamiliar functions.

Graphs as Diagnostic Tools

A graph provides immediate qualitative information about a function’s behavior. Before differentiating, students can examine features that indicate how a derivative should behave.

A graph that appears piecewise composed or non-smooth suggests careful attention to domain restrictions before applying rules.
Sharp corners or cusps indicate places where a derivative might fail to exist.
Curves exhibiting nested behaviors (e.g., waves within larger waves) often hint at composite structure, suggesting the chain rule may be appropriate.
Graphs showing products of oscillatory and polynomial behavior may indicate that both product and chain rules will be required.

When describing a graph’s shape, students rely on standard derivative interpretations. The slope of the tangent line, the instantaneous rate of change at each point, helps determine whether a chosen differentiation rule will produce the expected sign and magnitude.

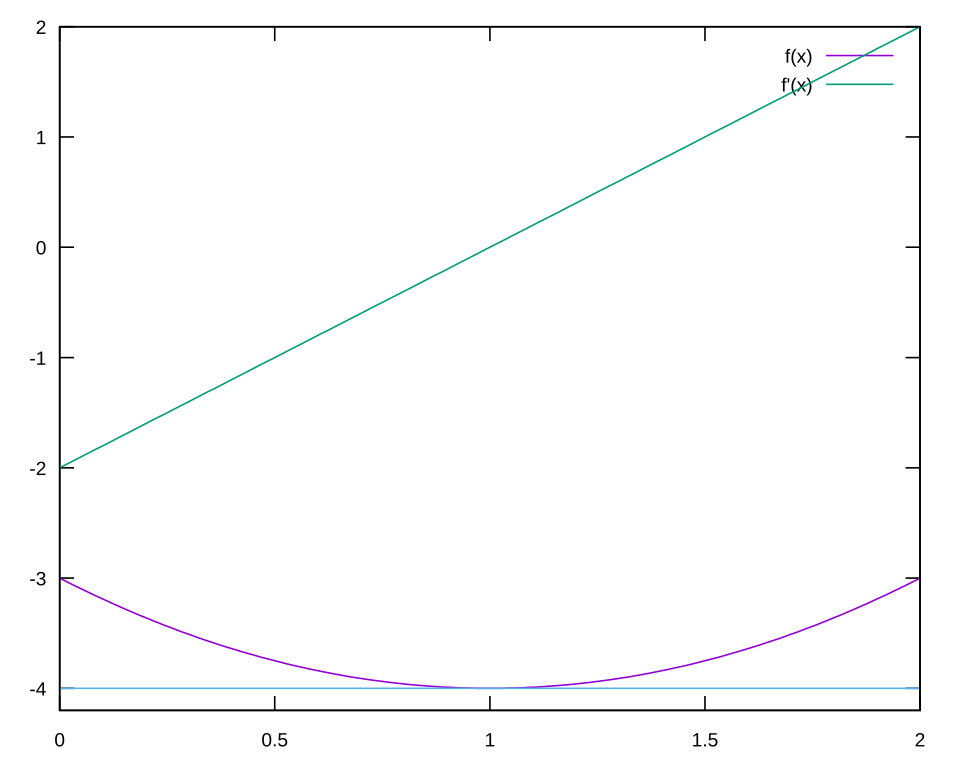
This graph displays the function $f(x)=x^2-2x-3$ , its derivative curve, and a tangent line at a specific point on the original function. The tangent line’s slope at that point matches the value of the derivative, illustrating the idea that the derivative gives the instantaneous rate of change. The separate derivative curve provides a visual way to compare the shape of $f$ and $f'$ when checking whether a computed derivative is reasonable. Source.

Slope of the Tangent Line: The instantaneous rate of change of a function at a point, equal to the value of its derivative there.

A graph allows a student to assess whether a derivative’s sign should be positive or negative, whether it should increase or decrease, and whether its magnitude should be relatively large or small. This prevents major errors when selecting or applying differentiation procedures.

Using Tables to Detect Patterns and Inform Rule Selection

Tables frequently appear in AP Calculus, showing values of a function $f(x)$ , its derivative $f'(x)$ , or related functions such as $g(x)$ and $g'(x)$ . Tables help students recognize patterns that reveal the internal structure of a function.

A table showing abrupt changes in slope magnitude may imply a product of varying growth rates, pointing toward the product rule. A table showing a consistently increasing slope may suggest the presence of a polynomial-like structure, while a changing sign pattern could indicate periodic or composite trigonometric behavior.

Tables allow students to:
- Detect whether a function is increasing or decreasing, supporting predictions about derivative sign.
- Identify maximums or minimums, suggesting derivative values of zero and assisting in checking analytic results.
- Infer composite relationships such as $f(g(x))$ when one table’s outputs seem to align with the inputs of another.

Tables also help verify results from implicit or inverse differentiation by confirming expected values of related functions.

Technology-Supported Differentiation and Verification

Graphing calculators and computer algebra systems (CAS) provide reliable ways to examine functions dynamically.

This photograph shows a TI-81 graphing calculator displaying the graphs of two functions, including $2\sin(X)$ and $X^3-2X$ , on the same coordinate grid. Such technology allows students to overlay functions, trace points, and approximate slopes, making it easier to judge whether a computed derivative or chosen differentiation rule is reasonable. The image also highlights that technology can graph more complicated expressions than those typically sketched by hand. Source.

Technology is particularly useful when:

The functional form is unfamiliar or too complex to inspect visually.
Multiple rules might apply, and students want to check consistency between methods.
Piecewise functions appear, and derivatives must be confirmed at boundary points.
A symbolic derivative is extremely complicated and requires numerical verification.

Technology also supports differentiation involving compositions, products, and quotients by allowing students to graph both the original function and its computed derivative to ensure qualitative alignment.

Numerical Derivative: An approximation of the instantaneous rate of change calculated by evaluating changes in function values over very small intervals.

Students must interpret technology-based outputs with mathematical understanding. Apparent flatness might be due to window settings, and oscillations may disappear at inappropriate scales. Thus, technology enhances but does not replace reasoning.

Deciding Which Differentiation Rule to Use

Together, graphs, tables, and technology provide evidence guiding the decision of which differentiation rules to apply.

Students may observe:

Composite behavior, such as nested curves, indicating the chain rule.
Multiplicative structure, where amplitude changes over oscillations hint at a product rule.
Ratios of functions, suggesting a quotient rule approach.
Implicit relationships visible from technology-generated plots, supporting implicit differentiation.

$f'(x) = \lim_{h \to 0} \dfrac{f(x+h) - f(x)}{h}$
$f(x)$ = Function value at $x$
$h$ = Increment approaching zero

Students use this formal definition conceptually to evaluate whether numerical or graphical evidence agrees with expected derivative behavior. A mismatch signals a needed revision in rule selection or symbolic computation.

Using Tools to Check Derivative Reasonableness

After completing a derivative analytically, students use visual and numerical tools to confirm:

The shape of the computed derivative matches the slope pattern of the original graph.
Values indicated by tables or technology align with computed formulas.
The derivative’s domain matches the behavior seen in graphs, especially at endpoints or discontinuities.

These checks reinforce correct differentiation strategies and deepen conceptual understanding.

FAQ

A poorly chosen viewing window can distort the apparent steepness or flatness of a curve. A function may appear to have a horizontal tangent when, in reality, the slope is small but non-zero.

Use multiple zoom levels to confirm behaviour.
Check the axes for equal scaling to avoid misinterpreting slope direction.
When in doubt, compare several screen views or use a numerical derivative tool.

Large fluctuations in the function’s values over small input intervals suggest sharp changes in slope.

If these changes alternate quickly between increases and decreases, the slope may vary rapidly.
Such behaviour warns you to examine the derivative more carefully, perhaps narrowing intervals or using technology to refine estimates.

Numerical differentiation is helpful for initial guidance but is sensitive to rounding and interval choice.

Small step sizes improve accuracy but may amplify calculator error.
Use numerical results as a diagnostic tool, not a final answer.
Always pair numerical checks with structural analysis of the function.

Visual similarity does not guarantee structural similarity. Two curves may appear alike yet arise from different compositions or multiplicative forms.

A function resembling a simple wave could be a composite of trigonometric and polynomial expressions.
Tables or symbolic forms help reveal hidden structures that graphs alone may obscure.

Compare the predicted slope trends from your derivative with the steepness observed on the graph.

If your derivative suggests rapid growth but the graph shows gradual increase, your expression may be overestimated.
Similarly, a derivative predicting small slopes where the curve is visibly steep indicates underestimation.
Use this comparison to refine your analytical work.

Practice Questions

Question 1 (1–3 marks)
A function f is shown on a graphing calculator screen. The graph appears to be decreasing for x < 1, then increasing for x > 1. Explain how technology can be used to verify whether the derivative f'(1) is approximately equal to 0, and state what feature of the graph supports this conclusion.

Question 1 (1–3 marks)
• 1 mark for stating that a graphing calculator or graphing technology can approximate the derivative numerically at x = 1.
• 1 mark for explaining that the slope of the tangent line or numerical derivative feature near x = 1 can be inspected.
• 1 mark for identifying that a turning point or change from decreasing to increasing suggests f'(1) is approximately 0.

Question 2 (4–6 marks)
A student uses a table of values for a function g and its derivative g' to determine which differentiation rules may be required to differentiate a related function h defined by h(x) = g(x) g(2x).
The table shows that g is increasing for x < 0, decreasing for 0 < x < 1, and increasing again for x > 1.
(a) Describe how a table of values helps the student infer whether g is likely to be composite, a product, or neither.
(b) Explain why examining changes in g' across different regions of the table can guide the student in selecting appropriate differentiation rules for h.
(c) State how graphical or technological tools could be used to check whether the resulting expression for h' is reasonable.

Question 2 (4–6 marks)
(a)
• 1 mark for explaining that a table of values helps detect changes in behaviour (e.g., increasing to decreasing) that may indicate structural features of g.
• 1 mark for noting that patterns in the table may suggest composite or multiplicative behaviour.

(b)
• 1 mark for stating that variations in g' indicate which differentiation rules may be needed when forming h'.
• 1 mark for explaining that the product h(x) = g(x) g(2x) implies the product rule and possibly the chain rule.

(c)
• 1 mark for stating that a graph or technological plot of h and h' can be used to compare slope behaviour.
• 1 mark for describing how consistency between the analytical derivative and graphical trends confirms reasonableness.

Try All Topic Practice Questions

Written by:

Dr Rahil Sachak-Patwa

Oxford University - PhD Mathematics

Rahil spent ten years working as private tutor, teaching students for GCSEs, A-Levels, and university admissions. During his PhD he published papers on modelling infectious disease epidemics and was a tutor to undergraduate and masters students for mathematics courses.