Using the Chain Rule in Related Rates (4.4.3) | AP Calculus AB Notes

AP Syllabus focus:
‘Apply the chain rule to differentiate equations relating multiple variables, ensuring that all derivatives are taken with respect to the same independent variable, usually time.’

Related rates problems require understanding how changing quantities connect. This topic explains why the chain rule is essential when multiple variables depend on time and must be differentiated consistently.

The chain rule is central to related rates because it ensures that every rate of change is expressed with respect to a single independent variable, typically time. When two or more quantities are linked by an equation, and each quantity changes as time progresses, differentiating correctly requires tracking how each variable depends on time. This prevents missing factors such as $\frac{dx}{dt}$ or $\frac{dy}{dt}$ that arise from implicit differentiation.

Why the Chain Rule Is Required

In related rates, expressions often involve composite functions—functions whose inputs also vary in time. Differentiating such relationships directly with respect to time demands the chain rule so that each variable’s dependence on time is fully represented. Because related rates problems do not treat variables as independent, it is incorrect to use ordinary derivative rules without accounting for how all quantities evolve over time. It is this interconnectedness that makes the chain rule indispensable.

The Role of an Independent Variable

Most related rates scenarios use time $t$ as the common independent variable. All rates, regardless of the physical or geometric setting, must be expressed in units per unit of time. When differentiating any expression involving a time-dependent variable, you must apply the chain rule automatically.

Independent Variable: The variable, typically time, with respect to which all derivatives in a related rates problem must be taken.

Because all changes are measured relative to the same independent variable, related quantities can be connected through their derivatives.

Differentiating Time-Dependent Quantities

When a variable such as $x$ depends on time, its derivative cannot be interpreted as $\frac{d}{dx}$ but instead as $\frac{dx}{dt}$ . Applying the chain rule ensures that implicit differentiation reflects this dependency even when it is not explicitly stated in the original problem. This is essential when equations include variables raised to powers, variables inside trigonometric or logarithmic functions, or variables multiplied together.

$\frac{d}{dt}[x^n] = n x^{n-1}\frac{dx}{dt}$
$x$ = time-dependent variable (units vary by context)
$n$ = constant exponent (unitless)

A sentence must appear between equation blocks to satisfy formatting rules. Differentiating more complex expressions similarly requires careful attention to each variable's dependence on time.

Applying the Chain Rule to Composite Expressions

Composite functions frequently arise in related rates through geometry, physics, and modeling contexts.

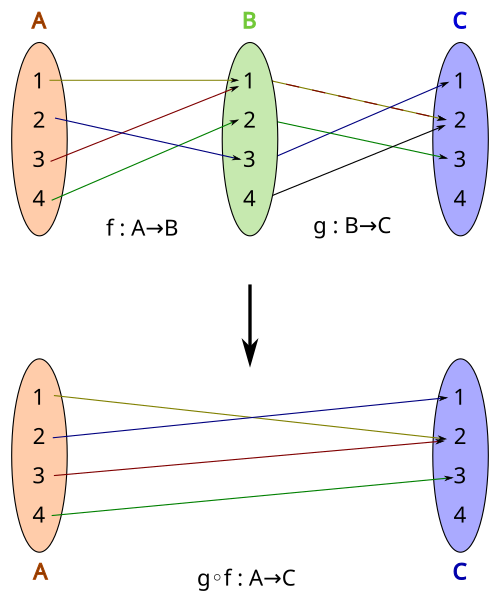
This diagram depicts the composition of two functions, showing how an input passes from set A through function $f$ to set B, then through function $g$ to set C. It illustrates how a single changing input affects multiple dependent outputs, reflecting the structure captured by the chain rule in related rates. The image contains only basic labels and arrows, with no extraneous detail. Source.

Whenever a formula involves a function within another function—such as a trigonometric function evaluated at a time-changing angle—the chain rule dictates that differentiation must reflect the inner function’s rate of change. Ignoring this structure leads to missing or incorrect rate expressions.

$\frac{d}{dt}[\sin(\theta)] = \cos(\theta)\frac{d\theta}{dt}$
$\theta$ = time-dependent angle (radians)

Such expressions appear in problems involving rotational motion, right-triangle relationships, or any scenario in which angles or lengths vary with time.

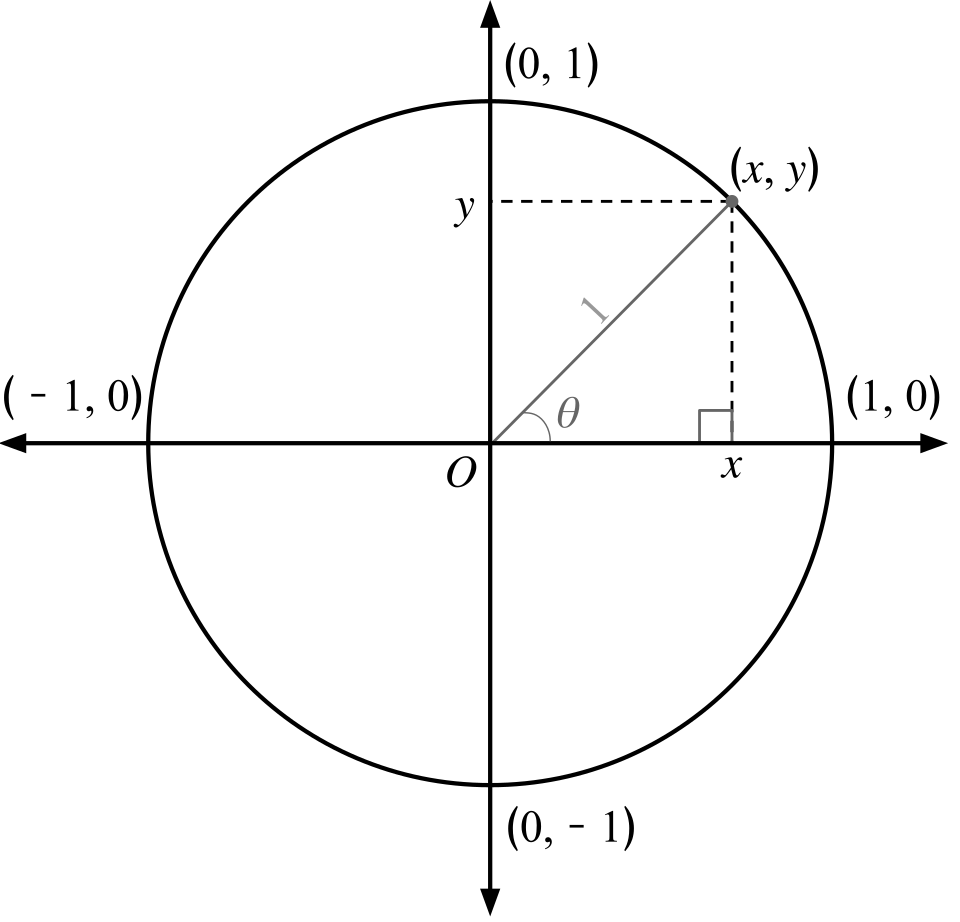
This unit-circle diagram shows an angle $\theta$ measured from the positive x-axis and a point on the circle with coordinates $(\cos\theta,\sin\theta)$ . It illustrates how a single time-dependent angle determines related horizontal and vertical components, each inheriting time dependence essential in related rates. The additional coordinate labels slightly exceed syllabus requirements but remain directly useful for trigonometric differentiation. Source.

Common Structures That Require the Chain Rule

In related rates, the chain rule is embedded within many routine differentiation steps. Students should be alert to these situations:

Powers of variables: Any expression of the form $x^n$ , $y^n$ , or combinations involving multiple time-dependent variables.
Trigonometric functions: Especially when an angle or input varies with time.
Logarithmic or exponential expressions: When the argument changes with time.
Geometric relationships: Equations involving radii, heights, distances, and angles that all depend on time.
Physical relationships: Quantities like pressure, force, temperature, or energy that change as underlying variables evolve.

Ensuring All Derivatives Are With Respect to Time

A frequent error in related rates problems is mixing derivatives with respect to different variables. To avoid this, every differentiation step should explicitly treat time as the independent variable. This means never using $\frac{dy}{dx}$ unless the problem specifically requires relating the rates $\frac{dy}{dt}$ and $\frac{dx}{dt}$ . Correct rate expressions must maintain consistent units that reflect changes per unit time.

Tracking Variables and Their Dependencies

Because multiple variables may change simultaneously, it is essential to label each rate clearly and express it with correct notation. The chain rule provides the framework for capturing how one variable’s rate influences another’s. When differentiating an equation that links several variables, each term must be examined to determine whether a product rule, quotient rule, or additional chain rule application is also required. This careful structure ensures accurate representation of how the related quantities interact through their time derivatives.

Interpreting Rates After Differentiation

Once differentiation is complete, the resulting derivative equation describes how all changing quantities are connected through their time rates. The chain rule ensures that each term in the equation reflects both the form of the original relationship and the way each variable evolves. Understanding this connection is fundamental to interpreting related rates results in meaningful context, aligned precisely with the AP Calculus AB expectations for this subsubtopic.

FAQ

Look for any variable whose value changes with time but appears inside another function, such as a trigonometric, exponential, or power function. This nested structure indicates that the derivative of the outer function must account for the inner variable's rate of change.

If the variable is part of a multiplication or division but is not inside another function, then product or quotient rules may be sufficient. However, many problems require combinations of these rules with the chain rule.

Time provides a natural, continuous measure of how physical, geometric, or functional quantities evolve. As objects move, grow, or change shape, time acts as the common factor linking their rates of change.

Using a single independent variable ensures consistency between all derivatives in a problem and allows different rates to be meaningfully compared and combined.

Yes. You may differentiate an implicitly defined relationship, such as one derived from a diagram or physical constraint. The chain rule still applies because each variable involved changes with time.

The key is to state the relationship correctly, even if it is geometric or verbal, before differentiating. Once written, apply implicit differentiation while treating every variable as a function of time.

Common errors include:
• Forgetting to multiply by the derivative of the inner variable with respect to time
• Mixing derivatives with respect to x, y, or t instead of staying consistent
• Substituting numerical values before differentiating, causing missing rate terms

To avoid these issues, always differentiate first, substitute later, and keep d(variable)/dt in every rate expression.

Quantities in diagrams often depend on one another through geometric formulas. As one measurement varies, others adjust according to the structure of the figure.

The chain rule ensures that when you differentiate these relationships, you capture how each interconnected variable contributes to the overall rate. This is especially useful when angles or lengths both change and influence each other’s behaviour.

Practice Questions

(1–3 marks)
A particle moves so that its position at time t satisfies an equation involving a time-dependent angle: y = 4 sin(theta), where theta is a differentiable function of time. Use the chain rule to find an expression for dy/dt in terms of theta and dtheta/dt.

(1–3 marks)
• 1 mark for recognising the need to apply the chain rule.
• 1 mark for differentiating sin(theta) correctly to obtain cos(theta).
• 1 mark for a fully correct expression: dy/dt = 4 cos(theta) dtheta/dt.

(4–6 marks)
A spherical balloon is being inflated. Its radius r increases with time according to an unknown differentiable function r(t). The volume of the balloon is given by V = (4/3)πr^3.
(a) Use the chain rule to differentiate V with respect to time, expressing dV/dt in terms of r and dr/dt.
(b) Explain why the chain rule is required in this situation.
(c) State what happens to the rate of change of volume if the radius increases at a constant rate, and justify your answer.

(4–6 marks)
(a)
• 1 mark for stating or identifying V = (4/3)πr^3.
• 1 mark for applying the chain rule to obtain dV/dt = 4πr^2 dr/dt.
(b)
• 1 mark for explaining that r depends on time, so differentiating V requires accounting for the rate of change of r.
(c)
• 1 mark for stating that dV/dt increases as the radius grows even if dr/dt is constant.
• 1 mark for justifying the statement by referring to the factor r^2 in the expression for dV/dt.

Try All Topic Practice Questions

Written by:

Dr Rahil Sachak-Patwa

Oxford University - PhD Mathematics

Rahil spent ten years working as private tutor, teaching students for GCSEs, A-Levels, and university admissions. During his PhD he published papers on modelling infectious disease epidemics and was a tutor to undergraduate and masters students for mathematics courses.