Product and Quotient Rules in Related Rates (4.4.4) | AP Calculus AB Notes

AP Syllabus focus:
‘Use product and quotient rules, together with the chain rule, when differentiating relationships between variables so that every term’s derivative is correctly expressed as a rate.’

Related rates problems often involve expressions where multiple time-dependent quantities multiply or divide, requiring careful differentiation using product and quotient rules to correctly relate their rates of change.

In many applied situations, two or more variables depend on time, even if the relationship between them appears algebraic and static. When a relationship involves multiplication or division, its structure forces the use of the product rule or quotient rule when differentiating with respect to time. Because related rates problems focus on how quantities change at an instant, these derivative rules ensure each differentiated term accurately represents a rate of change rather than a static quantity.

The need for these rules arises because each variable is itself a function of time. Even if time does not appear explicitly, the dependence is implicit, meaning every differentiation step must account for how each variable varies over time. This is why the specification emphasizes combining product and quotient rules with the chain rule, which guarantees that derivatives correctly include $\dfrac{d}{dt}$ for all time-dependent quantities.

Differentiation When Variables Depend on Time

Because related quantities change simultaneously, differentiating an expression such as $A = xy$ or $R = \dfrac{u}{v}$ requires acknowledging that $x$ , $y$ , $u$ , and $v$ all depend on time. Each derivative represents an instantaneous rate of change, which connects the physical or geometric meaning of the problem to a precise mathematical structure.

When differentiation introduces terms like $\dfrac{dx}{dt}$ or $\dfrac{dv}{dt}$ , these are interpreted as rates rather than slopes of static functions. Explicitly expressing these derivatives ensures no term is lost, and no variable is treated as constant unless the context guarantees it.

The product rule is essential when two time-dependent factors multiply to form a related quantity. Its structure ensures that both the change in the first factor and the change in the second factor contribute to the total rate of change. Neglecting even one component would cause an incorrect relationship between the quantities' rates.

Product Rule: When two differentiable functions of time multiply, their derivative is the derivative of the first times the second plus the first times the derivative of the second.

The product rule generates expressions containing both original variables and their time derivatives. In a related rates context, this supports accurate interpretation of how simultaneous changes combine to influence a dependent quantity.

Whenever your related-rates equation involves a product of two time-dependent quantities, you must apply the product rule so that each factor’s derivative appears in the rate equation.

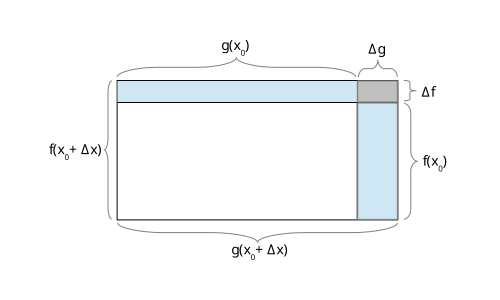
This diagram shows a rectangle whose side lengths represent two functions, and the shaded regions illustrate the contributions of $u'(x)v(x)$ and $u(x)v'(x)$ in the product rule. The figure includes minor proof-oriented elements beyond AP requirements but reinforces why both derivatives must appear in related rates. The visual structure emphasizes how simultaneous changes in each dimension produce the total rate of change of the product. Source.

$\dfrac{d}{dt}(xy) = x\dfrac{dy}{dt} + y\dfrac{dx}{dt}$
$x$ = Time-dependent variable
$y$ = Time-dependent variable
$\dfrac{dx}{dt}$ , $\dfrac{dy}{dt}$ = Rates of change of $x$ and $y$ with respect to time

These differentiated expressions demonstrate how multiple sources of change combine, making the product rule indispensable whenever a problem’s structure includes multiplication.

When one time-dependent quantity is divided by another, their relationship requires the quotient rule. This rule incorporates both the rate of change of the numerator and the rate of change of the denominator, while also accounting for how the denominator influences the magnitude of the resulting rate.

Quotient Rule: When one differentiable function of time is divided by another, the derivative is the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator, all divided by the square of the denominator.

Recognizing the quotient structure is crucial, because related rates problems using ratios often represent physical or geometric relationships—such as density, concentration, or velocity formulas—that change over time.

When a relationship is written as a quotient $Q(t)=\dfrac{N(t)}{D(t)}$ with both $N$ and $D$ depending on time, you must use the quotient rule to differentiate.

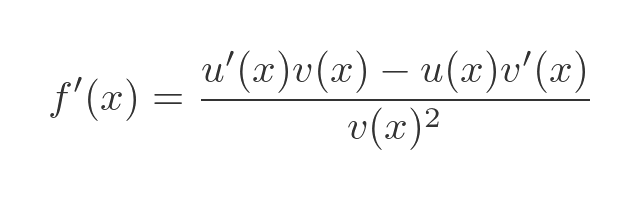
This formula graphic states the quotient rule in precise symbolic form, highlighting the numerator structure and the squared denominator. It reinforces correct organization of terms when forming related-rates equations. The image contains only the essential mathematical content needed for AP Calculus AB. Source.

$\dfrac{d}{dt}\left(\dfrac{u}{v}\right) = \dfrac{v\dfrac{du}{dt} - u\dfrac{dv}{dt}}{v^{2}}$
$u$ = Time-dependent numerator
$v$ = Time-dependent denominator
$\dfrac{du}{dt}$ , $\dfrac{dv}{dt}$ = Rates of change of $u$ and $v$ with respect to time

The quotient rule reinforces that both components of a ratio contribute to the instantaneous change, and that the denominator’s square is essential to maintaining correct scaling.

Integrating the Chain Rule with Product and Quotient Rules

Because each variable in a related rates problem depends on time, every derivative must apply the chain rule, even when it appears implicit. The chain rule ensures that differentiating an expression like $A = \pi r^{2}$ or $L = kx$ correctly introduces $\dfrac{dr}{dt}$ or $\dfrac{dx}{dt}$ , maintaining the essential link between static formulas and dynamic change.

The specification stresses using product and quotient rules together with the chain rule precisely because omitting the chain rule leads to relationships that ignore the time dependence central to related rates problems. In contexts involving physics, geometry, or real-world measurements, this alignment between structure and time variation is what makes related rates both powerful and broadly applicable.

Organizing Rate Expressions Correctly

Applying these rules requires careful notation and structured writing so that every term clearly expresses a rate. Students must distinguish between a quantity (such as $x$ ) and its rate ( $\dfrac{dx}{dt}$ ), avoiding confusion between instantaneous change and the quantity itself. Effective organization also prevents lost terms, sign errors, or incorrect assumptions of constancy.

Bullet-point strategies for maintaining accuracy include:

Identifying all time-dependent variables before differentiating.
Marking each derivative explicitly with $\dfrac{d}{dt}$ .
Checking whether multiplication or division is present before choosing a rule.
Ensuring that every final expression includes units consistent with rates.

FAQ

Look for any expression where two or more time-dependent quantities are multiplied. Even if one variable looks constant numerically, treat it as time-dependent unless the context explicitly states otherwise.
Common indicators include geometric formulas (such as area or volume components) or physical relationships where two changing measurements combine to produce a new quantity.

The quotient rule has a specific structure, and reversing the order of the numerator terms will give the wrong sign.
This matters because a sign error leads to an incorrect statement about whether the related quantity is increasing or decreasing.
A reliable memory aid is: derivative of the top times the bottom minus the top times the derivative of the bottom.

Yes. If a factor is explicitly constant in the context, you can pull it out before differentiating and avoid unnecessary product or quotient rules.
However, you must be certain from the problem statement that the factor does not change with time.
If there is any ambiguity, treat it as time-dependent and apply the appropriate rule.

Students often substitute numerical values too early. Always differentiate first, then substitute.
Other mistakes include failing to replace each variable with its given value, missing a sign on a derivative, or forgetting to square the denominator in the quotient rule.
Careful organisation of work reduces these errors.

After differentiating, check that:
• Every time-dependent variable has an associated rate term.
• No term that should contain a derivative is missing.
• The signs make sense with respect to the physical or geometric context.

A quick sanity check is to imagine whether the quantity should be increasing or decreasing under the given rates and compare this to the sign of your final expression.

Practice Questions

Question 1 (1–3 marks)
A quantity Q is defined by the product Q(t) = A(t)B(t), where A and B are differentiable functions of time t. At a particular instant, A = 5, dA/dt = 3, B = 4, and dB/dt = –2.
Find dQ/dt at that instant.

Question 1 (1–3 marks)

• 1 mark: States or uses the product rule in the form dQ/dt = A(dB/dt) + B(dA/dt).
• 1 mark: Substitutes correctly: dQ/dt = 5(–2) + 4(3).
• 1 mark: Correct final answer: dQ/dt = 2.

Question 2 (4–6 marks)
A variable Y is related to two time-dependent quantities U and V by the equation
Y(t) = U(t) / V(t).
Both U and V are differentiable functions of time.
(a) Derive an expression for dY/dt using the quotient rule.
(b) At a certain instant, U = 12, dU/dt = 5, V = 3, and dV/dt = –1.
Use your expression from part (a) to compute dY/dt at that instant.
(c) State whether Y is increasing or decreasing at this instant and justify your answer.

Question 2 (4–6 marks)

Part (a)
• 1 mark: Applies the quotient rule correctly: dY/dt = (V dU/dt – U dV/dt) / V².
• 1 mark: Uses correct structure, including the minus sign and the squared denominator.

Part (b)
• 1 mark: Correct substitution: (3(5) – 12(–1)) / 3².
• 1 mark: Correct computation: (15 + 12) / 9 = 27 / 9 = 3.

Part (c)
• 1 mark: States Y is increasing because dY/dt is positive.

Try All Topic Practice Questions

Written by:

Dr Rahil Sachak-Patwa

Oxford University - PhD Mathematics

Rahil spent ten years working as private tutor, teaching students for GCSEs, A-Levels, and university admissions. During his PhD he published papers on modelling infectious disease epidemics and was a tutor to undergraduate and masters students for mathematics courses.

Oxford University - PhD Mathematics

AP Calculus AB study notes

4.4.4 Product and Quotient Rules in Related Rates

Differentiation When Variables Depend on Time

Integrating the Chain Rule with Product and Quotient Rules

Organizing Rate Expressions Correctly

FAQ

Practice Questions

Hire a tutor

AP Calculus AB study notes

4.4.4 Product and Quotient Rules in Related Rates

The Role of Product and Quotient Structures in Related Rates

Differentiation When Variables Depend on Time

Applying the Product Rule in Related Rates

Using the Quotient Rule in Related Rates

Integrating the Chain Rule with Product and Quotient Rules

Organizing Rate Expressions Correctly

FAQ

Practice Questions

Hire a tutor