AP Syllabus focus:
‘Organize work by keeping track of variables, substitutions, and units, ensuring that final answers for related rates problems include appropriate units and reflect the context.’
Related rates problems require careful organization because multiple quantities change simultaneously, and each rate must be interpreted within a real context. Clear notation and consistent tracking of units help avoid errors and ensure meaningful final answers.
Structuring Related Rates Work
Organizing work in a systematic, transparent way is essential when differentiating relationships between changing quantities. Students must communicate clearly what each symbol represents, how variables relate, and why particular substitutions are made.
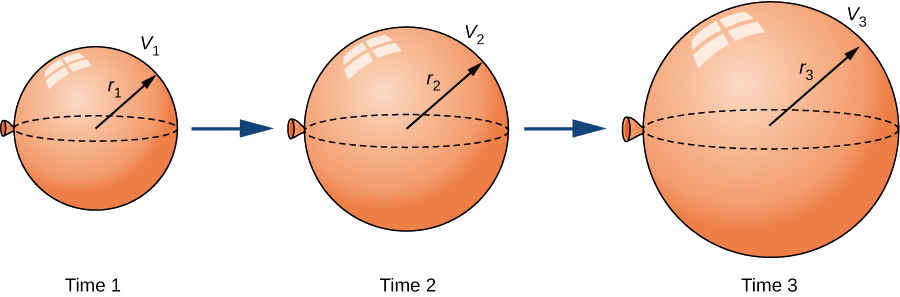
This diagram shows a balloon at three moments in time, with radius and volume labeled to illustrate how multiple quantities change together in a related rates setting. It highlights the need to identify variables clearly and associate each with proper units before forming equations. The diagram includes extra specifics such as timestamps, which simply reinforce careful variable labeling. Source.
Identifying and Labeling Variables
Before beginning any differentiation, it is crucial to define every changing quantity and specify how it relates to the situation.
Variable refers to a symbol representing a quantity that can change over time. When first introducing variables, they should be labeled directly on a diagram or in a written list so that each measurement has a clear physical meaning. Students should distinguish between independent variables and dependent variables, noting that time is usually the common independent variable in related rates problems.
Independent Variable: A quantity whose change is not determined by another variable in the relationship; in related rates, this is usually time.
After identifying variables, students should record the context-specific units associated with each quantity. This prevents later confusion when interpreting derivatives or forming equations.
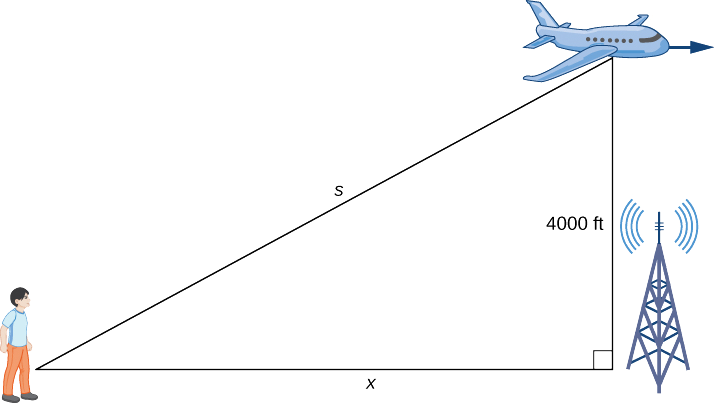
This right-triangle diagram shows distances labeled clearly, demonstrating how variables should be organized before differentiating a related rates equation. It highlights the importance of connecting geometric structure to variable definitions and units. The specific numbers exceed the general notes, but they provide a concrete illustration of structured variable labeling. Source.
A sentence describing the purpose of organization reinforces conceptual clarity and helps prepare for differentiating relationships correctly.
Stating Given Rates and Unknown Rates
All known rates of change must be written explicitly using derivative notation, such as , and matched with correct units. Students should indicate which rate is to be found, avoiding vague statements by specifying both the changing quantity and the instant at which it is measured.
Rate of Change: The derivative of a quantity with respect to time, representing how fast the quantity is increasing or decreasing at a specific moment.
This step ensures that the relationships among variables are understood before applying calculus techniques.
Writing Relationships Before Differentiation
A well-organized solution always includes the original equation relating the variables before taking derivatives. This equation must arise from geometry, physical principles, or contextual constraints. Students should avoid substituting numerical values until after differentiating so that the derivative accurately reflects all changing quantities.
A brief explanatory sentence between the equation and subsequent steps keeps the workflow logically ordered.
= Variables representing measured quantities with associated units
This symbolic relationship captures how quantities are connected prior to introducing their rates of change.
Differentiating with Respect to Time
Once the original equation is written, it should be differentiated implicitly with respect to time, ensuring every term’s derivative includes a rate such as or . Students must track unit consistency here because the units of a derivative always reflect output units divided by input units.
Implicit Differentiation: A differentiation method in which all variables are treated as functions of time, requiring multiplication by their corresponding derivatives.
After differentiating, the resulting equation should show how all rates relate within the situation, forming the basis for later substitution.
Substituting Known Information
Only after differentiating should numerical values be substituted into the derivative equation. Students must substitute both variable values and known rates, always carrying units through each expression. This prevents mixing incompatible quantities and helps confirm that the final result is physically meaningful.
A connecting sentence here reinforces that substitution must reflect the conditions at the specific instant described.
Solving for the Desired Rate
Rearranging the derivative equation isolates the unknown rate. Attention must be paid to the sign of the result, since positive and negative values convey meaningful directionality in real contexts. An organized workflow ensures the final equation retains unit integrity and maintains consistent interpretation.
Interpreting Units and Context in the Final Answer
The final step in a well-organized related rates solution is expressing the answer in a complete sentence that describes:
What quantity is changing
How fast it is changing
The direction or sign of change
The units consistent with the original context
Students should verify that the derived units match the structure of the rate. For instance, if a length is changing with respect to time, units should appear as distance per time. If an area or volume changes, units should naturally extend to square or cubic units per time.
A carefully written interpretation ensures that the mathematical result aligns with the physical or geometric situation, fulfilling the requirement that solutions reflect context accurately.
FAQ
A diagram should include every variable that changes with time and any fixed measurements essential to the relationship between quantities.
It does not need to be drawn to scale, but it must clearly show how the variables are connected so you can form an equation before differentiating.
Labels should include:
• Variable names
• Units (when known)
• Indicators of which quantities remain constant
A clean, well-labelled diagram reduces errors later when substituting values into differentiated equations.
Before writing any equation, list all quantities in the problem and mark each as either constant or variable.
A constant is a measurement that does not change over time, even if it appears in a geometric formula. A variable changes with time and therefore has an associated rate of change.
When forming the equation:
• Include constants without attaching rates
• Treat variables as functions of time
This prevents introducing unnecessary derivative terms.
Substituting numerical values too early removes the dependency between variables, causing important rate terms to disappear.
By differentiating first, you preserve how each quantity changes with time, ensuring every variable that should have a corresponding rate does.
After differentiation, substitution is safe because:
• The relationship between rates has already been established
• The numerical values now apply to one specific moment in time
This approach keeps the structure of the problem intact.
Maintain a dedicated units column or annotate units directly beside each variable and rate before starting calculations.
During differentiation, check that:
• Rates have units of output per time
• Combined units in expressions are consistent
• Units cancel or combine logically when solving for the unknown rate
After obtaining the final value, reattach units carefully. This acts as a reliability check on the reasonableness of the answer.
A negative rate indicates a quantity decreasing over time. The sign is not an error if it reflects the physical situation described.
To confirm correctness:
• Compare the sign with the direction of change in the context
• Check whether the variable in question is shrinking, draining, or moving towards a smaller value
• Ensure all orientation or direction conventions are consistent throughout the setup
Clear context interpretation prevents mislabelling a valid negative rate as a mistake.
Practice Questions
(1–3 marks)
A spherical balloon is being inflated. At a certain instant, its volume is increasing at 18 cubic centimetres per second. The radius of the balloon at that instant is 3 centimetres. State clearly what the given rate represents, including units, and identify the corresponding variable and its rate of change.
(1–3 marks)
• 1 mark for correctly identifying the variable as volume and the rate as dV/dt.
• 1 mark for stating that the rate represents how fast the volume is increasing at that instant.
• 1 mark for giving correct units: cubic centimetres per second.
(4–6 marks)
A particle moves along a straight line, and its distance x from a fixed point is increasing at 5 metres per second at a particular instant. At the same instant, a second quantity y, defined by the relation y = x² + 4, is changing.
(a) Write down the derivative dy/dt in terms of x and dx/dt.
(b) Evaluate dy/dt at the instant when x = 2 metres.
(c) Interpret the meaning of your answer to part (b), clearly identifying the units and what is changing.
(4–6 marks)
(a)
• 1 mark for differentiating y = x² + 4 correctly to obtain dy/dt = 2x(dx/dt).
(b)
• 1 mark for substituting x = 2 and dx/dt = 5 into dy/dt.
• 1 mark for obtaining dy/dt = 20.
(c)
• 1 mark for stating that y is increasing at 20 units per second at that instant.
• 1 mark for clearly identifying the correct units (units per second) and explaining that this represents the instantaneous rate of change of y with respect to time.

