Implicit relations let us study curves defined by equations linking x and y without explicitly solving for one variable, allowing powerful derivative-based analysis even when functions are not isolated.

Understanding Implicit Relations

An implicit relation connects x and y in a single equation without expressing either variable alone. In many real mathematical and applied situations, curves are not given by a simple formula such as $y=f(x)$ but instead arise from conditions that tie variables together. Unlike explicit functions, implicit relations may describe shapes or behaviors that cannot be rearranged into a single output variable, yet they remain analyzable with calculus techniques.

Implicit relations often describe curves such as circles, ellipses, and other geometric or algebraic shapes whose structure makes algebraic solving for y difficult or impossible.

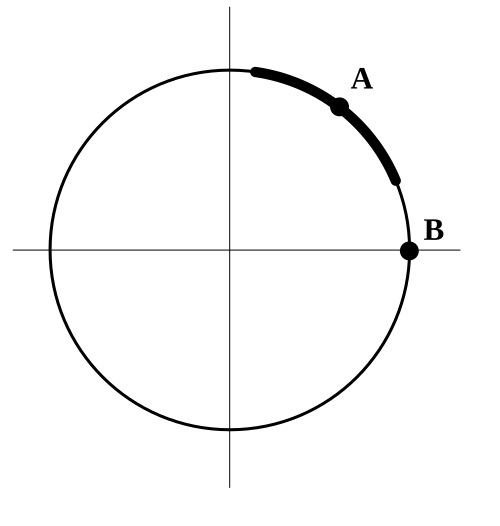
This diagram shows a circle defined implicitly by an equation such as $x^2 + y^2 = 1$, together with selected arcs and tangent segments. It illustrates how each point on the circle satisfies the same relation between $x$ and $y$, even though the circle as a whole cannot be written as a single explicit function $y=f(x)$. Extra details in the figure, such as labeled points and highlighted arcs tied to the implicit function theorem, extend beyond the AP Calculus AB syllabus but reinforce the idea that portions of the circle behave locally like explicit functions. Source.

Implicit relations often describe curves such as circles, ellipses, and other geometric or algebraic shapes whose structure makes algebraic solving for y difficult or impossible. Because AP Calculus frequently uses derivatives to interpret how graphs behave, understanding how to work with implicit forms is essential.

Distinguishing Implicit Relations from Explicit Functions

An explicit function expresses y directly as y = f(x), giving a single output for each domain value. However, many curves fail the vertical line test or contain multiple y-values for the same x, preventing explicit representation. Implicit relations avoid these difficulties by allowing equations that define sets of points without requiring functional form.

When Implicit Relations Are Necessary

Implicit forms appear naturally when:

• A relation describes geometric shapes with symmetric or multi-valued behavior.

• Solving for y leads to complicated expressions that obscure conceptual understanding.

• The algebraic form becomes more manageable when variables remain mixed.

Even though implicit relations do not explicitly give y, they still provide enough structure to analyze slopes, changing behavior, and connections between variables.

Viewing Implicit Relations as Curves

Any implicit relation can be interpreted as a set of points in the coordinate plane that satisfy its equation. This set typically forms a recognizable curve or set of curves. Understanding this viewpoint helps students interpret how calculus concepts apply to these shapes.

Graphical Interpretation

When a point $(x, y)$ makes an implicit equation true, that point lies on the curve described by the relation. Therefore, the full graph consists of all points that satisfy the given condition simultaneously. This graphical perspective allows students to reason about motion, shape, and behavior even without explicit formulas.

The classic example is the unit circle $x^2 + y^2 = 1$: for each x with −1<x<1, there are two y-values on the circle, one above and one below the x-axis.

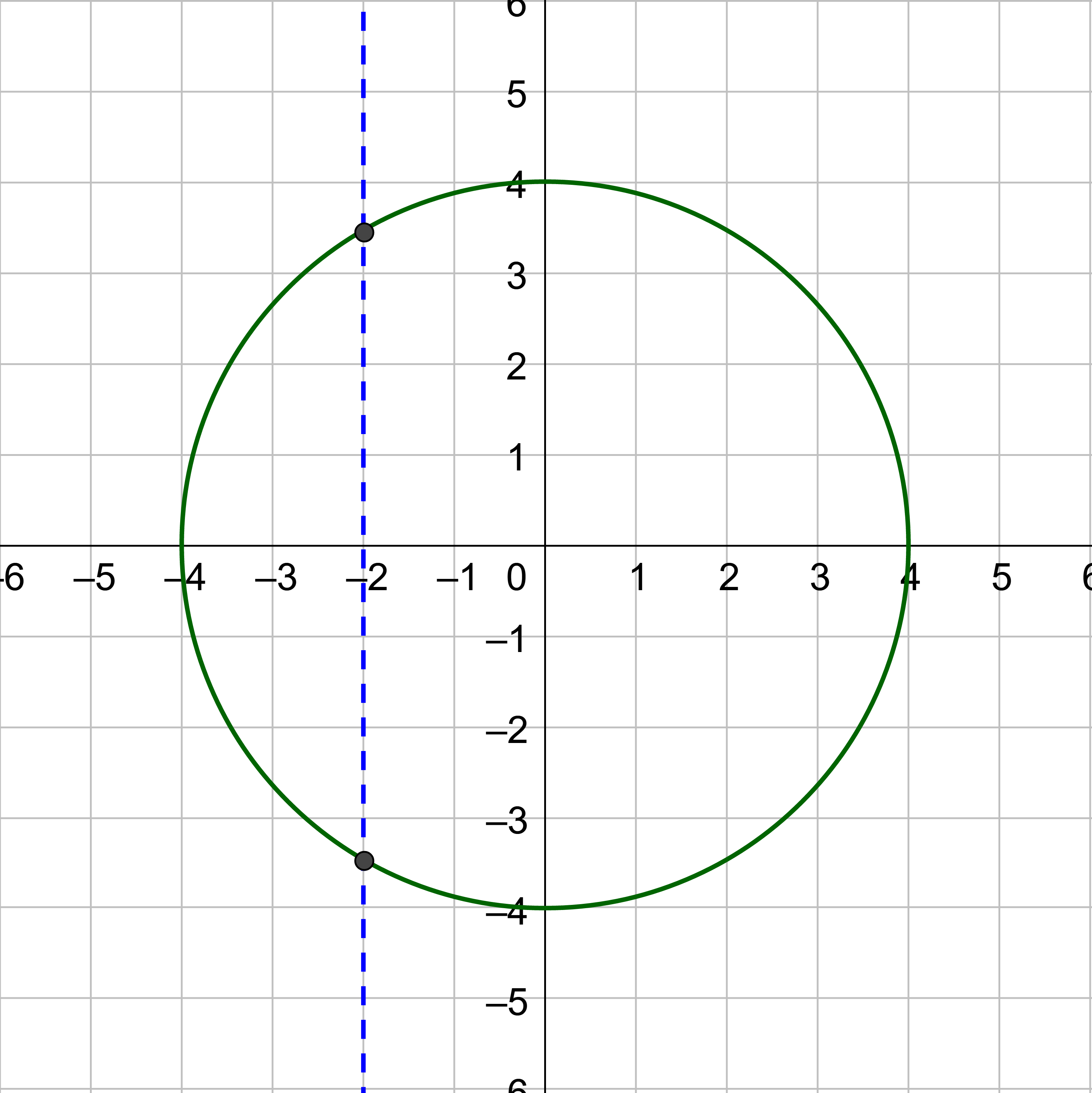
This graph shows a circle centered at the origin, which could be defined implicitly by an equation of the form $x^2 + y^2 = r^2$. For many $x$-values, the graph contains two points with the same $x$-coordinate but different $y$-coordinates, so it does not represent a single-valued function $y=f(x)$. The image focuses solely on the circle and grid, with no extra features beyond what is needed to illustrate failure of the vertical line test. Source.

Interpreting Behavior from Implicit Forms

Although implicit relations do not give slopes directly, derivative concepts remain central. Because y behaves as a dependent variable even when not isolated, calculus techniques treat y as a function of x behind the scenes. This enables powerful analytical tools for understanding the relation.

One of the most important insights is that an implicit equation still constrains how x and y change together. A small shift in x necessarily influences y, because both must continue to satisfy the relation.

Key Insights for Analyzing Implicit Relations

• A relation may define a full curve, multiple branches, or disconnected pieces.

• The behavior of the curve near a point is governed by how the equation links the variables.

• Derivative-based reasoning allows us to explore slopes and concavity even without solving for y.

• Understanding the underlying structure of the relation helps determine whether local behavior resembles that of a differentiable function.

A brief example of reasoning (without calculation) illustrates the idea: if an implicit relation defines a circle, each point on the upper semicircle behaves locally like part of a differentiable function, even though the entire circle cannot be written as one explicit formula.

Why Implicit Relations Matter in AP Calculus

Implicit relations highlight the broader idea that calculus tools apply beyond neatly packaged formulas. Students should recognize that many real phenomena—physical, geometric, or algebraic—are governed by constraints rather than explicit rules. This perspective broadens the usefulness of derivative concepts.

Benefits of Working with Implicit Relations

• They allow exploration of curves that cannot be handled algebraically in explicit form.

• They prepare students for related topics such as implicit differentiation and analyzing slopes.

• They reinforce understanding that derivatives describe relationships, not just formulas.

• They connect algebraic structures with graphical interpretations in a flexible way.

Implicit relations ultimately serve as a bridge between simple function-based calculus and more general mathematical analysis. Because the AP syllabus emphasizes understanding how these relations behave and how derivatives reveal their structure, mastering this topic provides essential groundwork for deeper study.