A curve defined implicitly can display rich behavior, and its first and second derivatives allow us to understand changes in slope, the presence of critical points, and the bending of the graph. These ideas parallel explicit differentiation but require additional attention because derivatives often depend on both x and y.

Interpreting Behavior from Implicit Derivatives

Understanding the Role of Derivatives in Implicit Relations

Implicit relations link x and y through an equation rather than a solved-out function, so their derivatives describe how the curve behaves locally. The first derivative indicates slope, while the second derivative reveals concavity and changes in how steepness develops. Even though the relation may not be written as $y=f(x)$, analyzing it mirrors the interpretation used for explicit functions.

Between derivatives and geometry lies a direct connection: slopes communicate direction, and concavity communicates curvature. These interpretations help determine whether the graph is rising, falling, bending upward, or bending downward at any given point on the curve.

Interpreting the First Implicit Derivative

The first derivative $\frac{dy}{dx}$ gives a point-by-point description of slope.

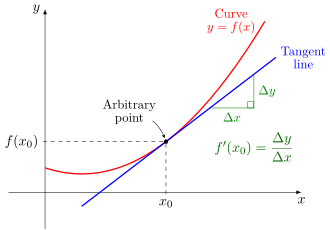
This diagram illustrates how a tangent line represents the instantaneous slope of a curve at a point. The tangent touches the graph once and shares its slope there. This same geometric interpretation holds for implicitly defined curves even when $y$ is not expressed explicitly as a function of $x$. Source.

Key uses of the first implicit derivative include:

• Determining where the curve has positive slope, meaning it rises as x increases.

• Identifying where the curve has negative slope, showing it falls as x increases.

• Locating horizontal tangents, when $\frac{dy}{dx} = 0$, which indicate momentary changes in direction.

• Identifying vertical tangents, when $\frac{dy}{dx}$ is undefined due to a zero denominator.

A normal sentence must appear here to maintain spacing between definition blocks and the remainder of the text. Interpreting this slope helps identify turning behaviors and transitions in how the curve progresses across its domain.

Connecting First Implicit Derivatives to Critical Points

For implicitly defined curves, a critical point occurs where $\frac{dy}{dx} = 0$ or where the derivative does not exist, provided that the point satisfies the original relation. These locations are essential when assessing local extrema or structural transitions on the curve.

To study critical points using implicit derivatives:

• Substitute candidate points into $\frac{dy}{dx}$ to verify whether the slope is zero or undefined.

• Confirm that each point lies on the implicit relation before considering it a true critical point.

• Use the sign behavior of $\frac{dy}{dx}$ around these points to interpret changes in direction.

A normal sentence between definition blocks ensures clear separation. These points act as anchors that shape the global behavior of the curve.

Using the Second Implicit Derivative to Understand Concavity

Second implicit derivatives are essential for interpreting how the slope itself changes. Because implicit relations mix x, y, and $\frac{dy}{dx}$, the second derivative often involves multiple layers of differentiation.

A single sentence appears here to maintain required spacing and to introduce how concavity and curvature reflect deeper features of the curve. Concavity describes whether the curve bends upward or downward at a point, based on the sign of the second derivative.

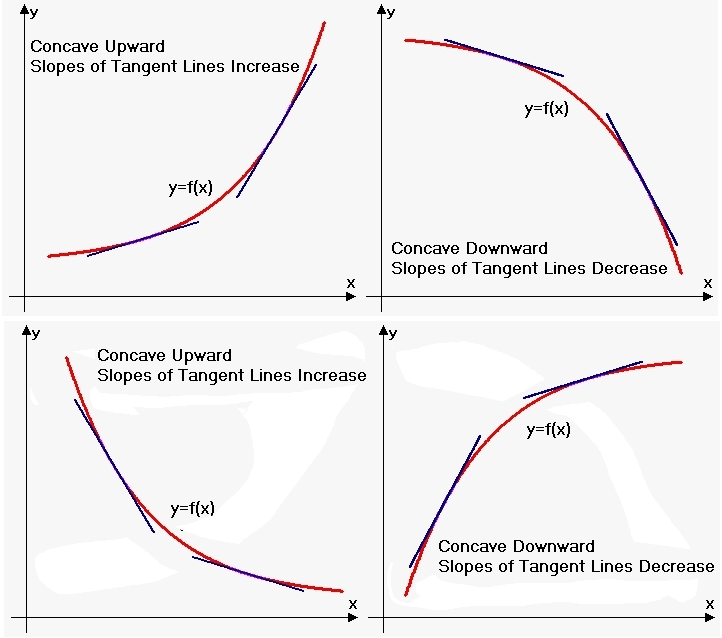
The diagrams compare concave up and concave down curves and illustrate how the slopes of tangent lines increase or decrease accordingly. These visual patterns connect directly to the sign of $\frac{d^2y}{dx^2}$. Although shown for explicit functions, the concavity–slope relationship applies equally to implicitly defined curves. Source.

Concavity interpretation guidelines:

• If \frac{d^2 y}{dx^2} > 0 , the curve is concave up, bending like a cup.

• If \frac{d^2 y}{dx^2} < 0 , the curve is concave down, arching over its domain.

• A change in sign of the second derivative suggests a potential inflection point, provided the curve is defined near that location.

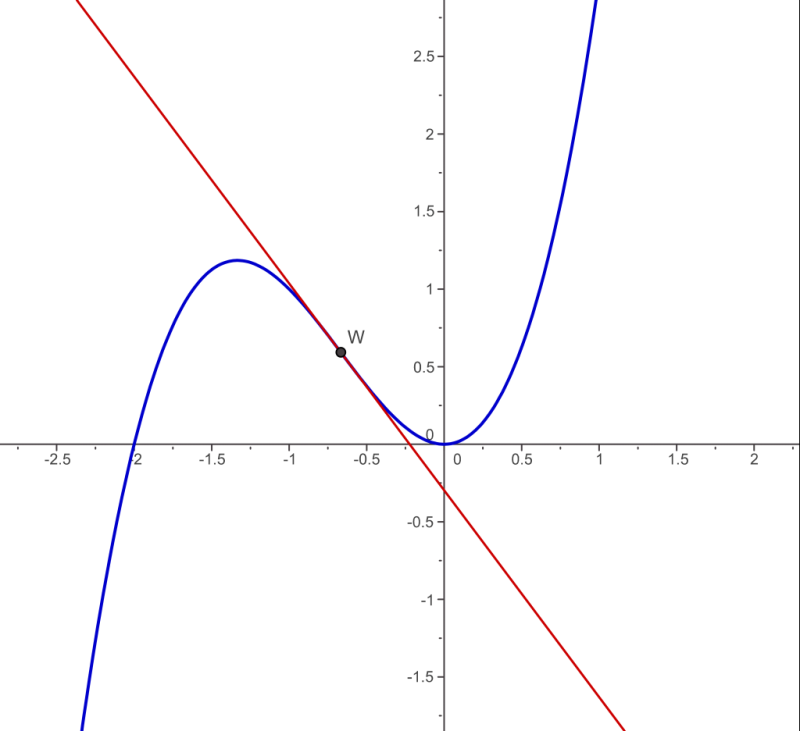
This graph shows a cubic curve changing concavity at a clearly marked inflection point. The curvature transitions from concave down to concave up as the second derivative changes sign. Although based on the function $x^3 + 2x^2$, the behavior illustrated is representative of any curve exhibiting an inflection point. Source.

Integrating First and Second Implicit Derivatives for Full Behavioral Insight

The combined information from the first and second derivatives provides a coherent description of how the curve behaves:

• Slope behavior from $\frac{dy}{dx}$ shows increasing or decreasing tendencies.

• Concavity behavior from $\frac{d^2 y}{dx^2}$ reveals how steepness changes.

• Critical points and curvature transitions together help map local maxima, minima, and inflection points, even when the function is not explicitly solved.

This detailed interpretation ensures that implicit curves can be analyzed with the same clarity and rigor as explicitly defined functions, aligning precisely with the expectations of the AP Calculus AB curriculum.