Analyzing implicitly defined curves requires extending familiar derivative-based reasoning to relations where y is not isolated. Students apply derivative tests to study extrema, behavior, and overall structure.

Applying Derivative Tests to Implicit Curves

Understanding Implicit Curves and Derivatives

Implicit curves appear when an equation involves x and y together without solving for y in terms of x.

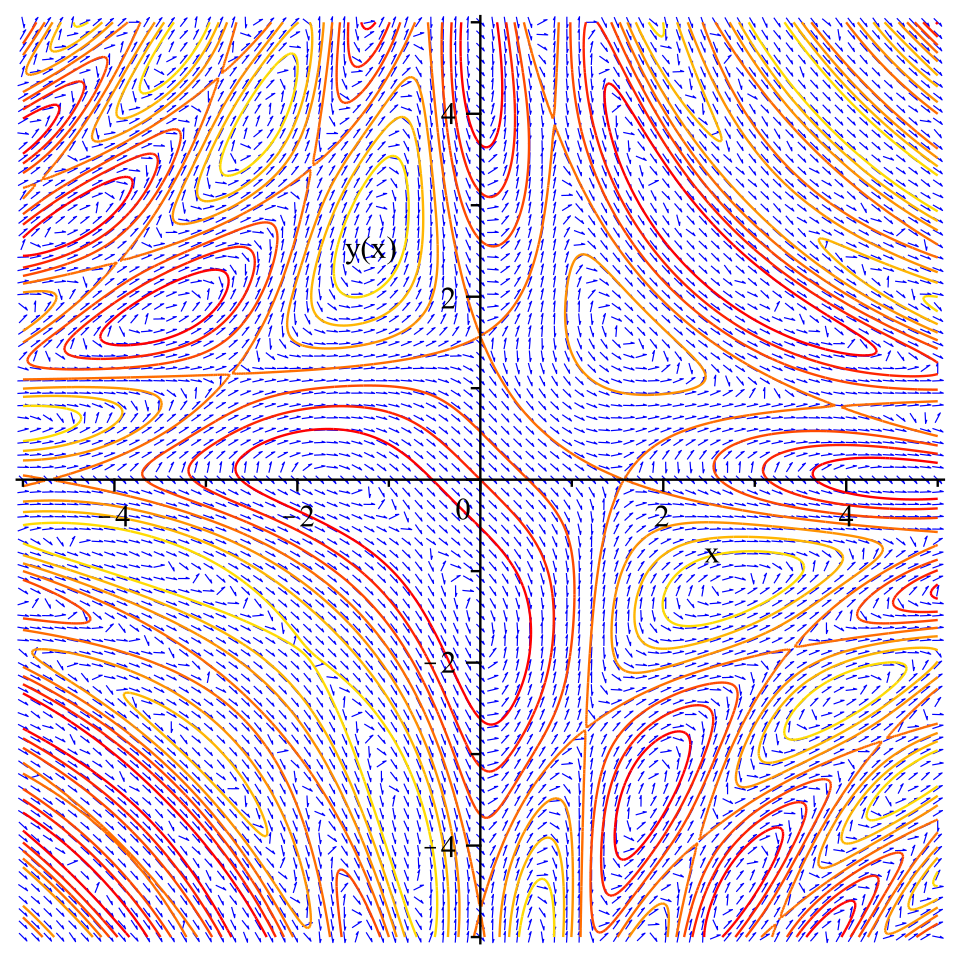
This graphic shows a family of curves defined implicitly by an equation of the form $f(x,y)=C$, displayed with a slope field to illustrate directions of $dy/dx$. The image highlights that implicit curves can behave locally like functions of $x$ with definable tangent directions. The figure includes more detail than required but reinforces how implicit derivatives guide local curve behavior. Source.

Because such relations may represent multiple branches or fail the vertical line test, analyzing their behavior requires differentiating implicitly to obtain derivative expressions that still describe local behavior.

Before applying derivative tests, the first step is always finding $dy/dx$ using implicit differentiation. This provides access to the slope of the tangent line, which is essential for determining extrema or behavior along the curve.

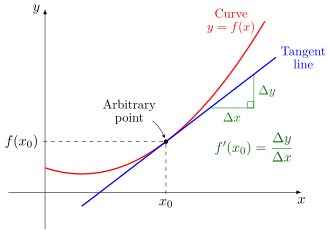
This diagram shows a curve and its tangent line at a specific point, illustrating how the derivative gives the instantaneous slope at that location. The tangent line approximates local behavior of the curve. Although shown for an explicit function, the same concept applies to implicitly defined curves. Source.

Once the first derivative is known, students can use standard tools—critical points, sign charts, and concavity tests—adapted to work with expressions involving both variables.

First Derivative and Critical Points on Implicit Curves

A critical point of an implicit curve occurs exactly where the derivative equals zero or does not exist, as long as the point lies on the curve itself. These points often represent potential local maxima, minima, or directional turning points on the implicit relation.

To locate critical points on an implicit curve:

• Solve the implicit equation to find coordinate pairs that lie on the relation.

• Compute the first derivative using implicit differentiation.

• Identify where the numerator of $dy/dx$ is zero (horizontal tangents).

• Identify where the denominator of $dy/dx$ is zero (vertical tangents), as long as the point is actually on the curve.

• Recognize that both types of points may contribute to the curve’s overall geometric behavior.

A horizontal tangent, where $dy/dx=0$, typically signals a potential local extremum in the y-direction. A vertical tangent shows undefined slope but may also correspond to crucial geometric transitions when analyzing the relationship.

Using Sign Charts for Implicit Derivatives

Although an implicit curve is not necessarily the graph of a single-valued function y=f(x), derivative tests still depend on the behavior of $dy/dx$ as x changes. Sign charts organize how the sign of the derivative varies along portions of the curve.

To analyze derivative signs for implicit curves:

• Express $dy/dx$ in simplified form involving x and y.

• Identify critical points and any discontinuities.

• Evaluate the sign of $dy/dx$ on portions of the curve by substituting representative points or analyzing component expressions.

• Use the resulting sign information to determine whether the curve rises or falls locally as you move along increasing x.

Because implicit curves may have multiple y-values for the same x, sign charts might require analysis across separate branches, emphasizing attention to domain segments where the relation behaves like a function.

Applying Extrema Classification to Implicit Relations

After locating critical points, students classify them using tools identical to those applied to explicit functions. The goal is to determine whether each critical point is a local maximum, local minimum, or neither, based on changes in derivative sign or concavity.

Two primary tests apply:

• First Derivative Test: Examine the sign of $dy/dx$ immediately before and after a critical point along each branch.

• Second Derivative Test: Compute and analyze $d^2y/dx^2$ using implicit differentiation to determine concavity if applicable.

Once the second derivative is computed, classify extrema using concavity criteria:

• Concave up near the point and $dy/dx=0$ suggests a local minimum.

• Concave down near the point and $dy/dx=0$ suggests a local maximum.

• Indeterminate concavity requires returning to the First Derivative Test.

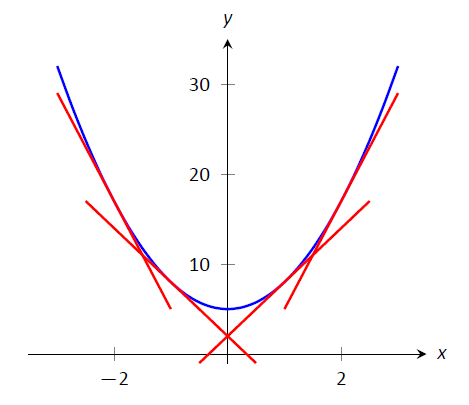
This figure illustrates how combinations of monotonicity and concavity determine the presence or absence of local extrema. The sign of $f'$ indicates whether a function is rising or falling, while the sign of $f''$ shows whether the curve bends upward or downward. The diagram includes more detail than required for this subsubtopic but reinforces how derivative signs classify extrema for both explicit and implicit curves. Source.

A normal descriptive sentence is required here before the next section, ensuring smooth conceptual flow for students transitioning between tests.

Interpreting Derivative Tests on Implicit Curves

Derivative tests for implicit curves help reveal geometric structure that may be hidden when the relation resists solving for y explicitly. Students use these tests to:

• Identify where the curve turns, bends, or changes behavior.

• Understand how multiple branches of an implicit relation connect or diverge.

• Justify claims about maxima, minima, and transitions in slope using derivative-based reasoning.

• Extend familiar calculus tools—even sign charts, extrema classifications, and concavity tests—to a broader class of curves than explicit functions alone.

These derivative-based insights ensure that implicit curves can be analyzed with the same rigor and structure expected throughout AP Calculus AB.