The Candidates Test provides a systematic, reliable procedure for identifying absolute extrema of a continuous function on a closed interval by evaluating a carefully chosen set of key points across the domain.

Understanding the Purpose of the Candidates Test

The Candidates Test is a structured method used to determine absolute maximum and absolute minimum values of a function on a closed interval. Because absolute extrema may occur either at interior points or at the boundaries of the interval, the Candidates Test ensures students examine all necessary locations where extreme values could emerge. This subsubtopic focuses specifically on the step-by-step process, emphasizing the importance of identifying critical points and evaluating the function at each candidate.

Requirements for Applying the Candidates Test

Before starting the procedure, AP Calculus AB students must recall that the Candidates Test is valid only when the function is continuous on a closed interval. If continuity fails or the interval is not closed, the conclusions of the test may not hold. A function that is continuous on an interval is guaranteed to have both an absolute maximum and an absolute minimum somewhere on that interval, but locating these extrema requires careful evaluation of candidate points.

Step-by-Step Process of the Candidates Test

The specification emphasizes that students must list all interior critical points and the interval endpoints, evaluate the function at each candidate, and compare these values.

This figure shows the graph of $y=\cos(3\pi x)/x$ on the closed interval $0.1\le x\le 1.1$, with its global and local maxima and minima clearly indicated. It illustrates how endpoints and interior critical points together form the full list of candidates for absolute extrema on a closed interval. The specific function and numerical labels extend beyond syllabus requirements but reinforce the Candidates Test procedure. Source.

Step 1: Identify and Confirm the Domain

To ensure the method can be applied correctly, begin by confirming the domain and verifying that the function is continuous on the relevant closed interval. This helps prevent overlooking any structural restrictions or undefined values that might affect analysis.

Step 2: Find All Critical Points Inside the Interval

A critical point occurs where the first derivative is zero or undefined, provided the value lies within the domain.

To locate these points within the interval interior:

• Compute the first derivative, ensuring the rules of differentiation are applied accurately.

• Solve $f'(x)=0$ to find potential interior candidates.

• Determine where $f'(x)$ fails to exist but the original function is defined.

• Retain only those points strictly inside the interval.

These interior critical points are essential candidates for absolute extrema because they represent positions where the function’s slope changes behavior or momentarily halts.

Step 3: Include the Interval Endpoints as Candidates

A central feature of the Candidates Test is the explicit inclusion of endpoints, because absolute extrema frequently occur at boundary values. Unlike local extrema, which do not rely on endpoints, absolute extrema may depend heavily on values at the boundaries. Students must therefore include:

• The left endpoint

• The right endpoint

No derivative conditions are required at endpoints for the purpose of this test.

Step 4: Evaluate the Function at All Candidates

Once all candidates have been identified, compute the function value at each one. This step involves evaluating the output of the original function, because absolute extrema depend on function values rather than derivative values. Students should maintain accuracy and keep track of all candidate evaluations clearly during this part of the process.

Step 5: Compare All Candidate Values

After computing values at all candidates, determine which is largest and which is smallest. These values represent the absolute maximum and absolute minimum of the function on the interval. This comparison finalizes the application of the test and provides a definitive answer supported by the systematic procedure.

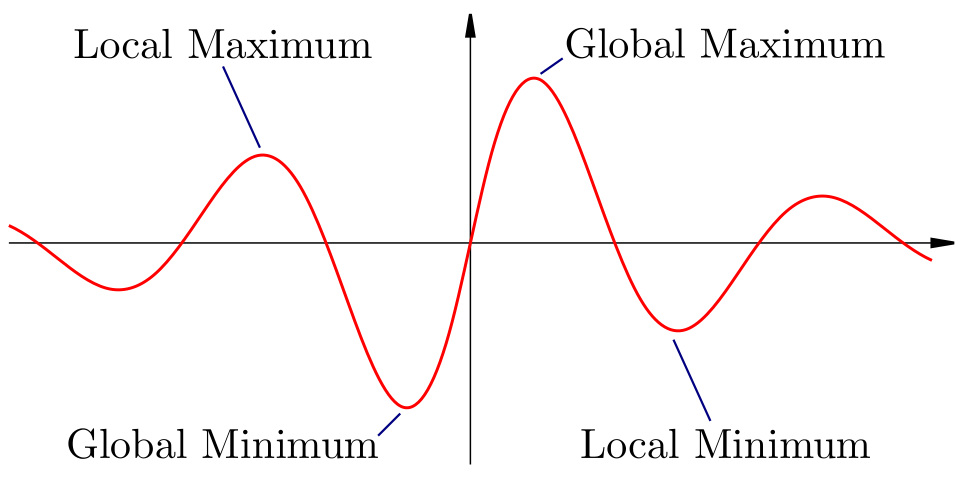
This diagram plots $y=\sin(x)\exp(-|x/5|)$ over a wide domain and labels several local maxima and minima along with the global maximum and minimum. It emphasizes that, after listing candidates, we must compare the corresponding $y$-values to determine which points are absolute extrema. The wide interval shown includes extra detail not required by the syllabus, but the labeling directly illustrates how global extrema differ from local extrema. Source.

Step 6: Justifying the Extrema

Even though the process is algorithmic, students must justify their claims by stating that each candidate was evaluated, including both endpoints and interior critical points. Correct justification strengthens mathematical communication and demonstrates understanding aligned with AP expectations.

Organizational Strategies for Applying the Candidates Test

Students can make the procedure more efficient by using structured approaches:

• Bullet lists of candidates help prevent omissions.

• Derivative sign checks ensure that critical points were found correctly, even though the Candidates Test does not require sign analysis.

• Clear notation for evaluations supports accuracy and logical structure.

These organizational methods support reliability in the results and align with college-level mathematical communication.

Why the Candidates Test Works

The Candidates Test relies on key properties of continuous functions on closed intervals. A continuous function on a closed interval achieves both its highest and lowest values, and these extrema must occur at either interior points where the derivative provides information or at boundary points where derivative information may be unavailable. Thus, examining both types of candidate points ensures that all possible locations for absolute extrema are considered.