A closed interval restricts where absolute maximum and absolute minimum values may appear, and identifying this limited set of possible locations helps streamline the search for global behavior.

Understanding Candidate Locations for Absolute Extrema on Closed Intervals

Absolute extrema on a closed interval $[a,b]$ arise from two distinct sources: interior critical points and the interval endpoints. This fact follows directly from the guarantee that continuous functions on closed intervals achieve both extreme values. The requirement of continuity plays a central role, ensuring that no gaps or jumps undermine the existence of extreme values within the domain.

When considering an interval such as $[a,b]$, students should emphasize the connection between the function’s differentiability and the identification of possible maxima or minima inside the interval. The key idea is that candidate points provide the finite list of locations where extrema must occur, allowing for systematic evaluation later in the Candidates Test.

Why Closed Intervals Guarantee Absolute Extrema

A closed interval includes its boundary points and avoids limiting behaviors that might occur as $x$ approaches but does not reach an endpoint. Because the Extreme Value Theorem applies only to functions continuous on a closed interval, the requirement that endpoints be included becomes essential. This guarantee lets us meaningfully check function values at those boundaries.

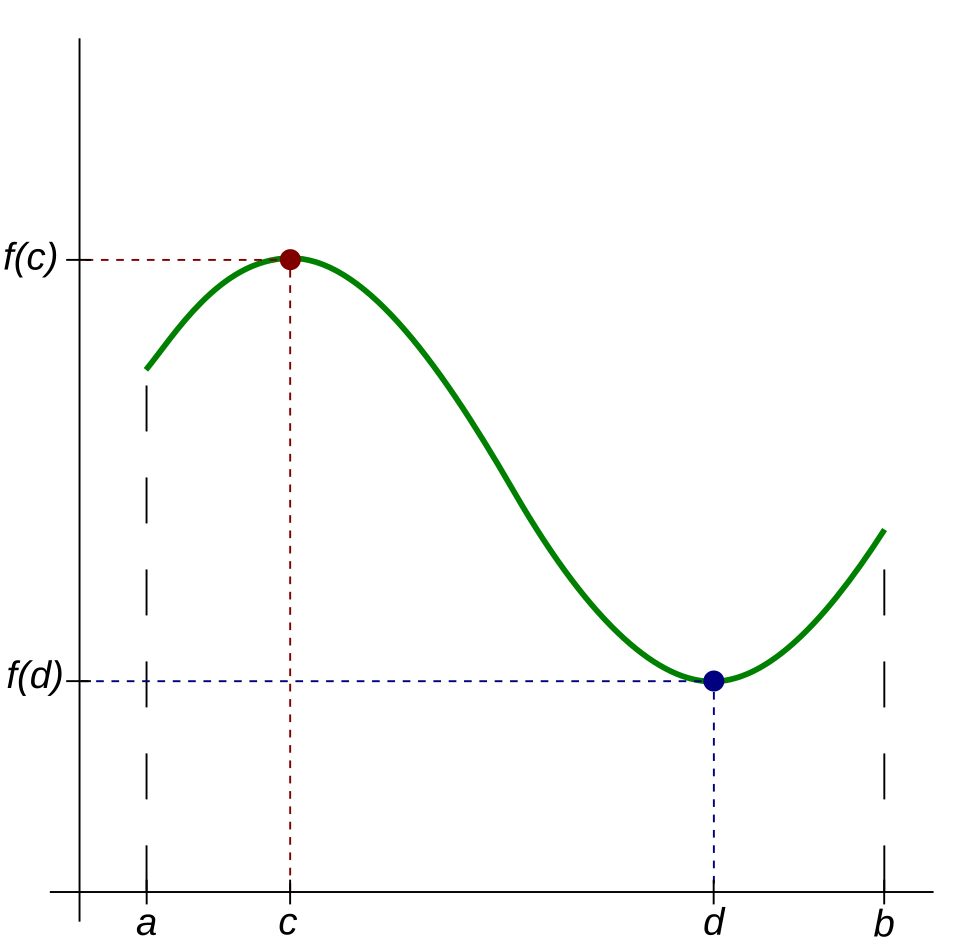
A continuous function on a closed interval $[a,b]$ is shown with its absolute maximum (red point) and absolute minimum (blue point) labeled clearly. The graph demonstrates that the function’s highest and lowest values are actually attained within the interval. The image aligns with the formal requirements of the Extreme Value Theorem without adding content beyond the AP Calculus AB syllabus. Source.

To proceed reliably in extremum analysis, it is important to maintain a clear understanding of the terminology used in this subsubtopic.

Any critical point lying strictly inside $(a,b)$ is a candidate for an absolute extremum, but critical points alone do not determine which type of extremum appears. More investigation is always required.

Because definitions cannot carry the entire conceptual load, the relationship between extrema and interval structure must also be emphasized.

Candidate Types for Absolute Extrema

Two distinct categories of candidates must always be checked when analyzing absolute extrema on a closed interval:

Interior Critical Points

Interior points are those strictly within $(a,b)$. If the derivative at an interior $x$-value satisfies $f'(x)=0$ or does not exist, the point qualifies as a candidate. Only interior critical points serve this role; derivative behavior at endpoints is irrelevant because endpoints are not interior.

Endpoints of the Interval

Even though they are not critical points (since the derivative is not evaluated from both sides), $a$ and $b$ must still be checked. This requirement arises because the absolute maximum or minimum could occur at a boundary even when no local extremum exists there.

The Structure of Candidate Identification

When determining where absolute extrema may occur on a closed interval, students should adopt a systematic approach. The goal is not yet to decide which candidate produces the maximum or minimum but only to identify all possible locations on the domain where they could occur. Reliable problem solving begins with assembling a complete list.

Key steps include:

• Confirming continuity on the closed interval before beginning any extremum analysis.

• Locating interior critical points by checking where $f'(x)=0$ or where $f'(x)$ fails to exist within $(a,b)$.

• Including the endpoints $a$ and $b$ as necessary candidates regardless of derivative behavior.

• Avoiding extraneous points outside the domain or at open boundaries, since extrema may not exist there.

Through this structured method, the identification process remains logically consistent and guided directly by the course specification.

Importance of Continuity and Domain Restrictions

Because the Extreme Value Theorem hinges on continuity across $[a,b]$, a function that violates continuity may fail to achieve an absolute extremum. If a discontinuity interrupts the domain, then limits or boundary behavior may not correspond to actual function values. Students should recognize that candidate identification depends not only on derivatives but also on the domain itself.

Following the syllabus, this subsubtopic deliberately focuses on where extrema can occur, not on how to determine which candidates produce extrema. That classification occurs in later subsubtopics, but here the emphasis remains strictly on assembling the correct candidate list.

Structural Logic Behind Candidate Inclusion

In the search for absolute extrema, interior critical points and endpoints exhaust all possibilities because:

• A differentiable point in the interior where the derivative is nonzero indicates the graph is either strictly increasing or strictly decreasing at that location, preventing the point from being an extremum.

• Points outside the interval are irrelevant because the extremum must occur on $[a,b]$.

• Endpoints require evaluation because growing or shrinking behavior of the function may reach a maximum or minimum precisely at one of the boundaries.

This structural constraint ensures students do not overlook potential extrema simply because endpoints are not interior or because derivative information may be unavailable there.

Organizing Candidate Points in Practice

To maintain clarity, students can list candidates using a structured format:

• Interior critical points in $(a,b)$

• Left endpoint $a$

• Right endpoint $b$

Each point in this list captures one of the only possible locations for an absolute extremum on the closed interval. This enumeration sets the foundation for evaluating the function later and comparing results to determine which values represent the largest and smallest outputs over $[a,b]$.

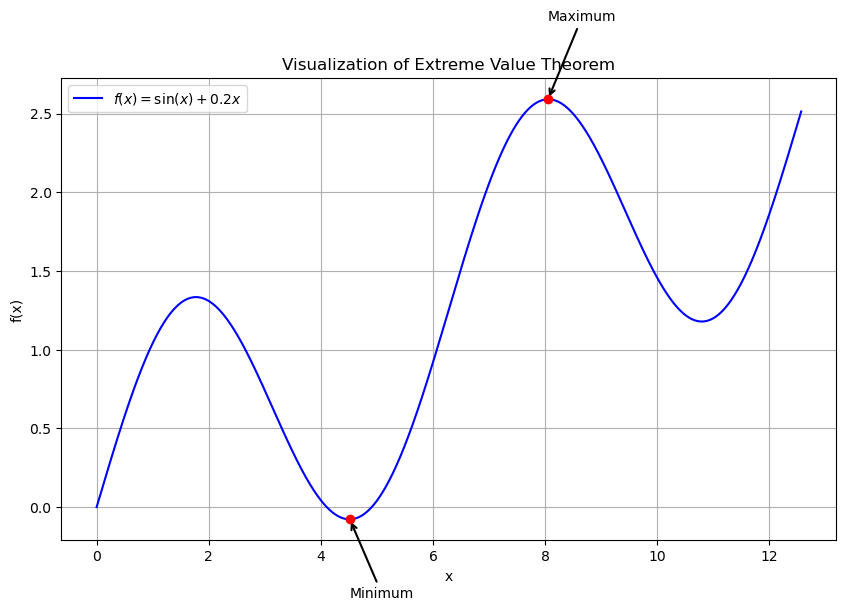
The graph of $f(x)=\sin(x)+0.2x$ on a closed interval is shown with the absolute maximum and minimum indicated by red points labeled “Maximum” and “Minimum.” One extremum lies at an interior point while the other occurs at an endpoint, illustrating how candidates arise from both critical points and boundaries. The visual matches AP-level expectations without introducing concepts beyond the syllabus. Source.