AP Syllabus focus:
‘Before applying the Candidates Test, confirm the function’s domain and that the interval is closed; otherwise, absolute extrema might not exist or may occur at boundary points not included.’
Understanding how to check the domain and interval conditions is essential before applying the Candidates Test, ensuring that absolute extrema are identified correctly and interpreted within the proper mathematical constraints.
The Importance of Verifying Conditions
Before using the Candidates Test, students must ensure that all required hypotheses are satisfied. The test only works when the function is continuous, the domain is properly defined, and the interval is closed. These conditions guarantee that absolute extrema exist and that every appropriate candidate is considered.
Domain Considerations for Extrema
Why the Domain Matters
The domain of a function is the set of all input values for which the function is defined. Extrema cannot occur at points outside this set, and ignoring domain restrictions can lead to incorrect conclusions.
Domain: The set of all real -values for which a function is defined.
A function’s domain may be restricted by operations such as division by zero, even roots of negative numbers, logarithms of nonpositive numbers, or contexts from applied problems. Because absolute extrema must occur within the domain, the domain must be checked before listing candidates.
How Domain Restrictions Affect Extrema
Domain limitations influence which points qualify as valid candidates for extrema. Discontinuities, undefined points, and endpoints outside the domain invalidate the use of the Candidates Test unless adjustments are made.
Normal sentence here to maintain required spacing.
Closed Interval Requirements
Role of Closed Intervals
A closed interval includes its endpoints and is written using brackets. When applying the Candidates Test, the function must be continuous on such an interval. This setting ensures that a continuous function attains both an absolute maximum and an absolute minimum within the interval.
Closed Interval: An interval of the form that includes both endpoints and .
When an interval is not closed, one or more boundary points may not be part of the domain, and extrema may fail to exist even if the function behaves nicely elsewhere.
Normal sentence here to maintain required spacing.
To apply the Extreme Value Theorem, the function must be continuous on a closed interval , so that absolute extrema are guaranteed to exist somewhere in that interval.
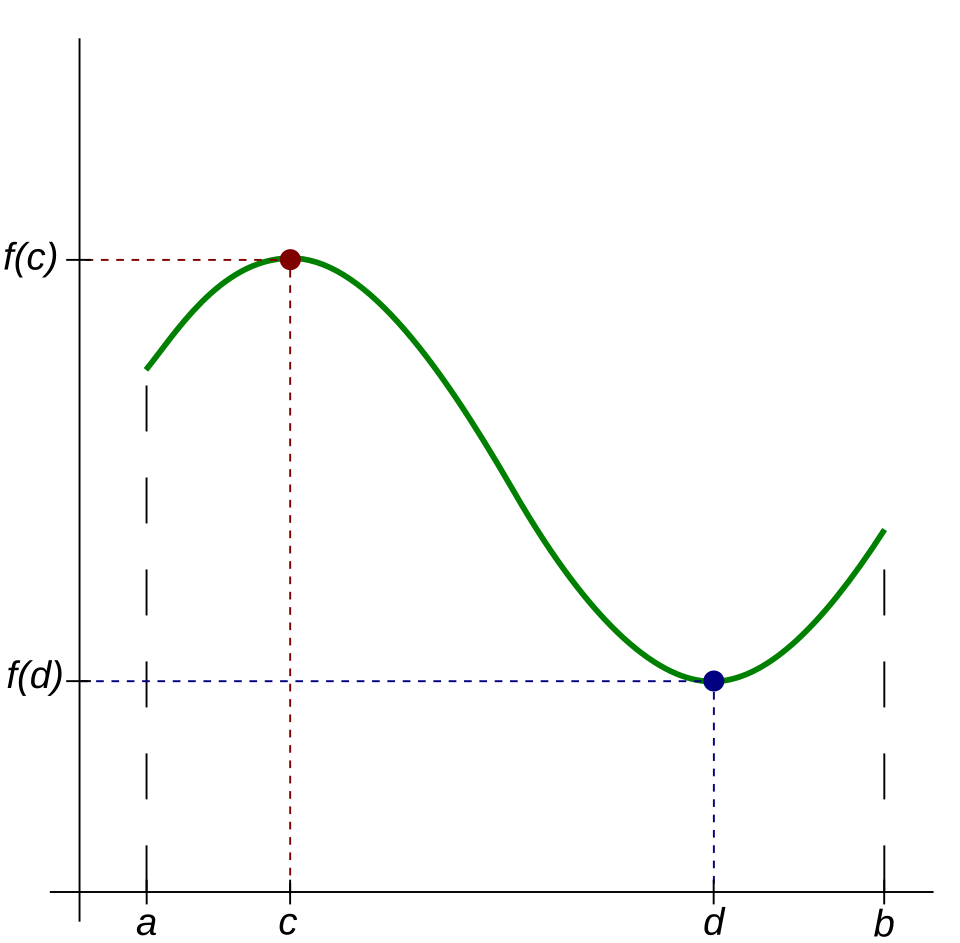
A continuous function on a closed interval with clearly identified absolute extrema. This visual demonstrates the Extreme Value Theorem, which ensures that a continuous function on a closed interval must attain both an absolute maximum and an absolute minimum. The extrema may occur at interior points or endpoints, illustrating why all such points must be included in the Candidates Test. Source.
Consequences of Missing Conditions
Extrema May Fail to Exist
If a function is not continuous on the closed interval or if the interval endpoints are excluded, the guarantee of the Extreme Value Theorem does not apply. As a result, the process of identifying absolute extrema becomes incomplete or unreliable.
Boundary Points and Missing Endpoints
When endpoints are excluded or undefined, potential extrema at those locations cannot be considered. For example, a function that approaches a value near an endpoint without ever attaining it cannot use that limiting behavior as an extremum.
Verifying Function Continuity
Why Continuity Is Required
The Candidates Test assumes the function is continuous on the interval. Discontinuities can create breaks where extrema could occur but are not captured by derivative-based approaches.
Continuity: A function is continuous at a point if its value, limit, and limit-based approach all agree.
Students should recognize that if the function is not continuous on the closed interval, the Candidates Test may not provide complete information about extrema.
Normal sentence here to maintain required spacing.
Step-by-Step Verification Process
Essential Checks Before Applying the Candidates Test
Use the following checklist to confirm whether the Candidates Test can be applied effectively:
Identify the domain of the function and check for restrictions.
Confirm that the given interval is closed, ensuring that both endpoints are included.
Verify continuity on the entire closed interval.
Ensure all endpoints lie within the domain, since endpoints outside the domain invalidate the interval.
Confirm that any interior discontinuities are addressed, since they can affect whether extrema exist.
Proceed to the Candidates Test only after all conditions hold, ensuring that identified extrema are valid.
How These Checks Influence the Result
Each step ensures that all possible extrema—including those at endpoints—are valid and accounted for. If any condition is violated, the absolute maximum or minimum may not exist or may occur at a boundary point that is excluded from consideration.
Before applying the Candidates Test, confirm the function’s domain and that the interval is closed; otherwise, absolute extrema might not exist or may occur at boundary points not included.
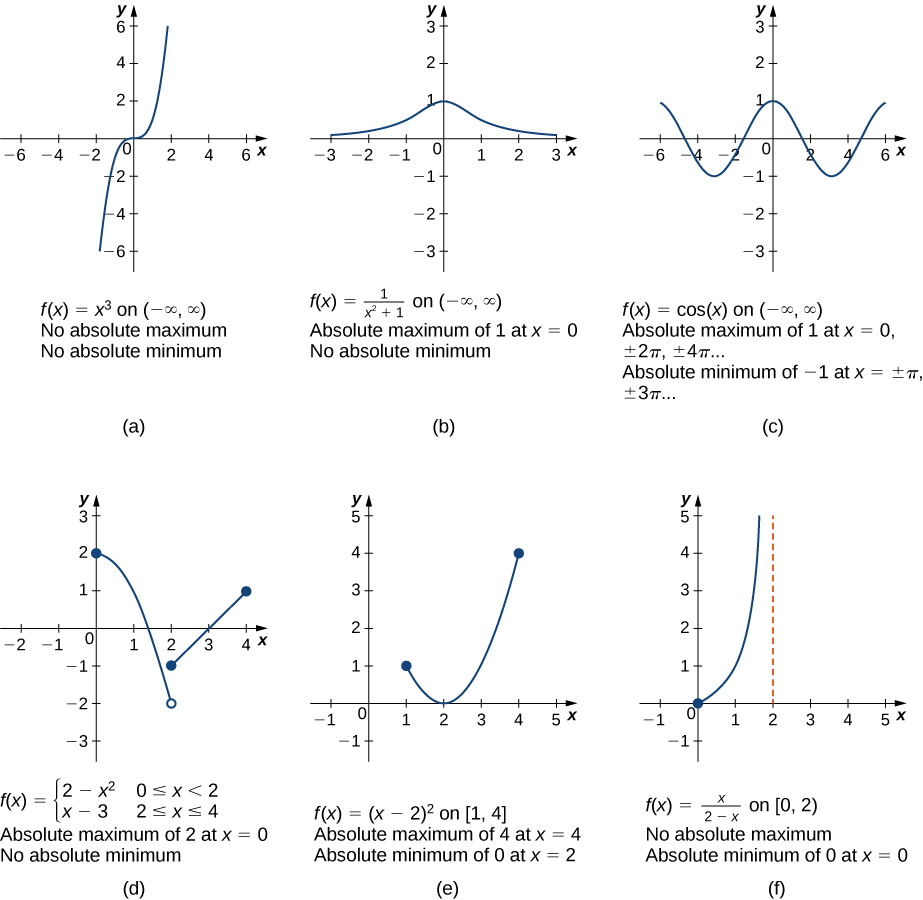
A set of contrasting graphs illustrating when absolute extrema do and do not exist. Some functions are continuous on a closed interval and possess both extrema, while others lack extrema because of open intervals or discontinuities. Several functions shown extend beyond the AP syllabus, but all effectively demonstrate how domain and interval restrictions determine whether absolute extrema occur. Source.
Interpreting Outcomes When Conditions Fail
Adjusting the Approach
When the domain or interval fails to satisfy the required conditions, students must rely on other methods. Open intervals require analyzing limits approaching endpoints. Discontinuous functions may need piecewise inspection.
Maintaining Logical Justification
Clear justification requires explicitly referencing domain and interval conditions when explaining why the Candidates Test applies. When these conditions do not hold, the explanation must clarify how this affects the existence and identification of extrema.
Using These Conditions in Applied Contexts
Real-World Constraints
Applied problems often include physical or contextual limitations that modify the domain. Interpreting extrema correctly involves ensuring that domain restrictions align with the real-world scenario being modeled.
Ensuring Mathematical and Contextual Consistency
Students must evaluate whether the mathematical conditions for extrema coincide with practical constraints, reinforcing a coherent understanding of the Candidates Test’s assumptions.
FAQ
Check whether the function is defined at the endpoint. If the function value does not exist, the endpoint cannot contribute a maximum or minimum.
If a function approaches a finite limit at an excluded endpoint but never attains it, that limiting value does not count as an extremum. The Candidates Test only applies to points where the function is actually defined.
If a domain restriction creates a hole or asymptote inside the interval, the interval is no longer suitable for automatic application of the Candidates Test.
You may still analyse the function, but you must treat the interval as effectively split into separate parts. The missing point means that absolute extrema may fail to exist, even if both pieces behave normally.
Continuity guarantees that the function does not jump, break, or approach a value without reaching it. This ensures that any extremum that should exist actually occurs within the interval.
A function with even one discontinuity inside the interval may approach, but not attain, maximum or minimum values, preventing certainty about absolute extrema.
Yes. If the function is continuous on a closed interval, an absolute extremum may occur at a cusp, corner, or other nondifferentiable point.
Such points still qualify as valid candidates. The derivative is not required to exist; the only essential condition is continuity on the closed interval.
The problem must be reformulated. You cannot apply the Candidates Test to an interval that includes points where the function is undefined.
Possible adjustments include:
• Narrowing the interval to match the function’s actual domain.
• Treating the interval as open or half-open, understanding that absolute extrema may no longer be guaranteed.
The domain always defines the true boundaries for extremum analysis.
Practice Questions
A function f is defined on the interval [0, 5]. Before applying the Candidates Test to find absolute extrema, a student notes that f is not defined at x = 5.
Explain why the Candidates Test cannot be applied on [0, 5].
Question 1 (1–3 marks)
• 1 mark: Identifies that the interval [0, 5] is not closed for the function because f is not defined at x = 5.
• 1 mark: States that the Extreme Value Theorem requires continuity on a closed interval to guarantee extrema.
• 1 mark: Concludes that the Candidates Test cannot be applied because the theorem’s conditions are not met.
Total: 3 marks
A function g is continuous for all real numbers except at x = 2. The function is defined on the interval [1, 4], and its derivative is given by:
g'(x) = (x - 3)(x - 1)
a) State all candidate x-values that must be checked when attempting to find the absolute maximum and minimum of g on [1, 4].
b) Explain why g cannot be guaranteed to have an absolute maximum and minimum on [1, 4].
c) Describe how the lack of continuity at x = 2 affects the use of the Candidates Test on the interval.
Question 2 (4–6 marks)
a) (2 marks)
• 1 mark: States that critical points occur when g'(x) = 0, giving x = 1 and x = 3.
• 1 mark: Identifies the endpoints x = 1 and x = 4 as candidates (note: x = 1 listed twice is acceptable if justified as both a critical point and an endpoint).
b) (2 marks)
• 1 mark: States that g is not continuous at x = 2, which lies inside the interval.
• 1 mark: Explains that without continuity on the entire closed interval, the Extreme Value Theorem does not guarantee absolute extrema.
c) (2 marks)
• 1 mark: Explains that the discontinuity at x = 2 prevents the secure use of the Candidates Test because the function may fail to attain extrema.
• 1 mark: Notes that values near the discontinuity may approach maxima or minima without ever being reached, so the test does not fully apply.
Total: 6 marks

