AP Syllabus focus:
‘Explain how a positive rate over an interval gives a positive accumulated change, while a negative rate gives a negative accumulated change for the quantity.’
Accumulated change measures how a quantity increases or decreases over an interval by interpreting the area under its rate-of-change graph. Positive and negative rates determine the direction of change.
Understanding Accumulated Change
Accumulated change connects a varying rate-of-change function to the overall change in a quantity over time. When a rate is represented graphically, the area between the graph and the x-axis provides a visual measure of how much the quantity has increased or decreased.
Accumulated Change: The total net change in a quantity over an interval, found by interpreting the signed area between a rate-of-change graph and the x-axis.
Because accumulation depends on signed area, the sign of the rate plays a central role in determining how the quantity evolves across an interval.
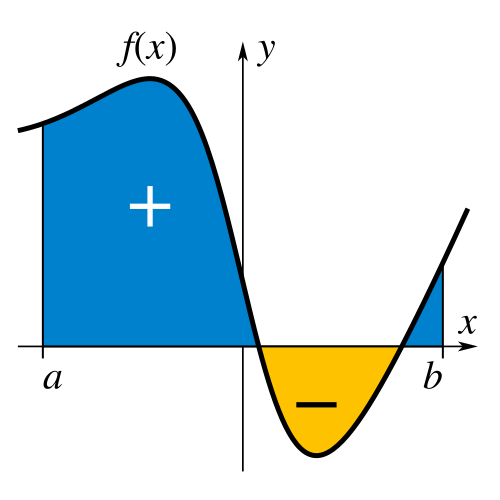
This graph of shows the area above the -axis shaded and labeled with a plus sign, and the area below the -axis shaded and labeled with a minus sign. It emphasizes that regions where the rate is positive contribute positive accumulated change, while regions where the rate is negative contribute negative accumulated change. The particular curve and interval are not important; they simply serve as a generic example of signed area in integration. Source.
Positive Rates and Positive Accumulated Change
A positive rate of change indicates that the underlying quantity is increasing. On a graph, this corresponds to the rate function lying above the x-axis. The area above the axis contributes positively to accumulated change.
Why a Positive Rate Produces Positive Accumulated Change
When the rate is positive on an interval:
The graph of the rate function remains above the x-axis.
Each small piece of area represents a positive contribution to total change.
Summing these contributions yields a positive accumulated change.
The underlying quantity ends the interval at a higher value than it started.
Interpreting Positive Accumulated Change in Context
Positive accumulated change reflects an overall gain in the quantity being measured. In real-world situations, a positive net change may indicate:
Increased distance traveled
Growth in volume or mass
Rise in population
Increased amount of a resource over time
Even if the rate is not constant, any portion of the graph above the x-axis increases the accumulated change. This illustrates the idea that accumulation depends on sign, not merely magnitude.
Negative Rates and Negative Accumulated Change
A negative rate of change indicates that the quantity is decreasing. Graphically, the rate function lies below the x-axis, producing negative contributions to total change.
Why a Negative Rate Produces Negative Accumulated Change
When the rate is negative on an interval:
The graph falls below the x-axis.
Each small slice of area is treated as negative area, meaning it subtracts from total accumulation.
Summing these values results in negative accumulated change.
The underlying quantity ends the interval at a lower value than it began.
Interpreting Negative Accumulated Change in Context
Negative accumulated change signals an overall loss in the quantity. Situations that produce negative accumulation include:
A tank draining faster than it fills
A velocity function representing movement in a negative direction
Decreasing mass, population, or concentration
Any rate representing consumption or removal
Even when the rate varies, any interval where the graph is below the axis contributes to a net decrease in the underlying quantity.
Mixed Positive and Negative Rates
Many real-world scenarios involve rate functions that cross the x-axis, switching between positive and negative values. This causes accumulated change to reflect the net effect of increases and decreases.
Net Change from Signed Areas
When interpreting such graphs:
Positive regions contribute positively to accumulated change.
Negative regions contribute negatively.
The total accumulated change equals the sum of signed areas, not the total geometric area.
The final value of the quantity may increase or decrease depending on which contribution dominates.
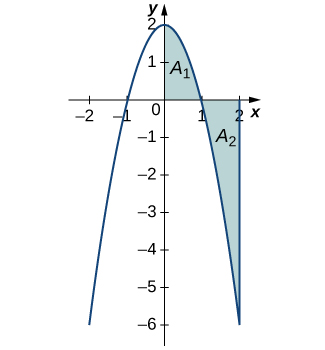
This figure shows a curve crossing the -axis, with the region above the axis labeled and the region below labeled . It illustrates that the definite integral over the interval represents the net signed area, conceptually understood as . The explicit labels exceed the syllabus wording slightly but reinforce how positive and negative accumulated changes combine. Source.
Between intervals, it is essential to distinguish net change from total variation, because only net change accounts for the sign of each region.
Graphical Features That Indicate Positive or Negative Accumulation
When reading a rate-of-change graph, the following features determine the sign of accumulated change:
Position Relative to the x-Axis
Above the x-axis: contributes positive area and increases accumulation.
Below the x-axis: contributes negative area and decreases accumulation.
Intervals of Constant Sign
If the rate remains strictly positive, accumulated change must be positive.
If the rate remains strictly negative, accumulated change must be negative.
Intervals Where the Graph Crosses the Axis
When the graph crosses the axis, the sign of the rate changes. Important observations include:
Crossing points mark transitions between increasing and decreasing accumulation.
The magnitude of the area on each side determines whether net change is positive or negative.
The accumulated change function experiences changes in slope but remains continuous as long as the rate function is continuous.
Conceptual Significance of Signed Area
The concept of signed area distinguishes accumulated change from purely geometric area. This distinction is necessary because accumulated change expresses how a quantity evolves, not how large the region under the curve is.
Signed area ensures that:
Increases and decreases counteract each other, producing a meaningful measure of net change.
The sign of the rate is preserved in the calculation of accumulation.
Accumulation aligns with intuitive interpretations of growth or decay.
Even when the rate varies, any interval where the graph is below the axis contributes to a net decrease in the underlying quantity.
This velocity–time graph shows an object moving forward at a constant positive velocity and then backward with a constant negative velocity. The shaded regions demonstrate how positive velocity produces positive accumulated displacement and negative velocity produces negative accumulated displacement. The specific speeds are extra contextual details, but the image clearly illustrates how signed rates determine signed accumulated change. Source.
FAQ
A quantity decreases overall when the negative portions of the rate graph have a larger total signed area than the positive portions.
Even if the rate becomes positive at times, those positive contributions may be too small to offset the negative areas. The result is a net negative accumulated change.
Yes. Accumulated change is zero when the total positive area equals the total negative area.
This means the increases and decreases perfectly balance out, leaving the final value unchanged despite the rate varying across the interval.
When the rate graph touches the x-axis, the rate is momentarily zero, meaning the quantity is neither increasing nor decreasing at that instant.
Touching the axis does not contribute positive or negative area. Only intervals strictly above or below the axis affect the accumulated change.
Short negative intervals subtract from accumulated change, but their effect depends on their magnitude.
• A small negative rate over a short time produces only a minor negative contribution.
• If surrounded by larger positive regions, its impact on net accumulation may be negligible.
Geometric area measures size only, while signed area preserves directional information.
Accumulated change requires understanding not just how large the rate is but whether it increases or decreases the quantity. Signed area ensures decreases counteract increases, producing a meaningful measure of net change.
Practice Questions
(1–3 marks)
A rate of change function r(t) is shown to be entirely below the t-axis on the interval 0 ≤ t ≤ 5.
State whether the accumulated change of the quantity over this interval is positive, negative, or zero, and briefly justify your answer.
(1–3 marks)
• 1 mark: States that the accumulated change is negative.
• 1 mark: Justifies that the rate is below the axis, so the signed area is negative.
• 1 mark: Recognises that a negative rate over the entire interval implies the quantity decreases overall.
(4–6 marks)
A particle moves along a line, and its velocity v(t) (in metres per second) is given graphically. On the interval 0 ≤ t ≤ 8, v(t) is positive on 0 ≤ t ≤ 3, negative on 3 < t ≤ 6, and positive again on 6 < t ≤ 8.
(a) Explain whether each sub-interval contributes positively or negatively to the particle’s change in position.
(b) The total area above the t-axis is 12 square units and the total area below is 7 square units. Determine the net change in position over the interval and state whether the particle ends up ahead of or behind its starting position.
(c) Briefly explain the meaning of a negative contribution in the context of this motion.
(4–6 marks)
(a)
• 1 mark: Correctly identifies that 0 to 3 contributes positively.
• 1 mark: Correctly identifies that 3 to 6 contributes negatively.
• 1 mark: Correctly identifies that 6 to 8 contributes positively.
(b)
• 1 mark: Calculates net change as 12 − 7 = 5 units.
• 1 mark: States the particle ends ahead of its starting position (positive net displacement).
(c)
• 1 mark: Explains that a negative contribution represents movement in the opposite direction or reduction in position relative to the starting point.

