This subsubtopic emphasizes how units behave when interpreting area under a rate function, helping students understand why accumulated change carries compound units determined by both the rate and the horizontal axis.

Understanding Units in Accumulated Change

Interpreting accumulated change begins with recognizing that a rate function expresses how one quantity changes with respect to another. When you take the area under a rate graph, you are effectively summing tiny contributions of rate multiplied by time or another independent variable. This creates new, combined units that describe the total change of the quantity being measured.

The Structure of a Rate Function

A rate is a quantity that compares how one variable changes relative to another, such as velocity (meters per second) or flow rate (liters per minute). These forms always carry the unit pattern “units of output per unit of input.”

When this rate is graphed against its input variable on the horizontal axis, the area between the graph and the axis represents accumulated change.

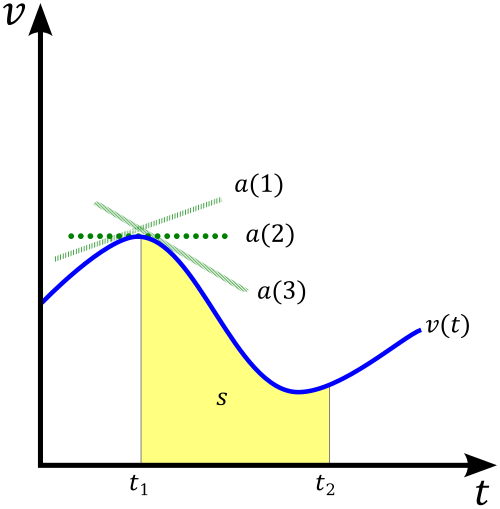
This graph plots velocity on the vertical axis and time on the horizontal axis, with the shaded area representing the object’s displacement. The units of the shaded area are “velocity units × time units,” matching the accumulated change in position. The graph also hints at acceleration as the slope of the line, which is extra context beyond this subsubtopic but consistent with later calculus and physics applications. Source.

Understanding the independent variable ensures that students correctly associate the width of the “rectangles” in a Riemann sum with the appropriate units, allowing accurate unit multiplication.

Why Area Produces Combined Units

The area under a rate graph is computed conceptually as the sum of infinitely many products: each small rectangle has height equal to the rate value and width equal to a small change in the independent variable.

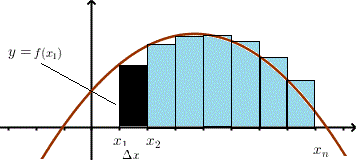
This figure shows a function $y = f(x)$ with several narrow rectangles whose heights are function values and whose widths are $\Delta x$. The total area under the curve is approximated by summing the areas $f(x_i)\Delta x$, which combines “output units per input unit” with “input units” to produce the units of accumulated change. The surrounding text on the source page discusses limits and definite integrals, which goes beyond this subsubtopic, but the visual itself is focused on the geometric idea of rate times interval length. Source.

Multiplying these produces units that immediately reflect accumulated change.

This expression shows that area is not merely a geometric concept; it becomes a meaningful physical or contextual quantity when applied to rate functions.

It is important for students to see that accumulated change always inherits its units directly from the structure of the rate itself and the variable being accumulated over.

Identifying Units in Applied Settings

Determining Units from Rate Information

To correctly identify accumulated change units, students should analyze both components of the rate expression. If the rate is stated verbally, graphically, or algebraically, the same principles apply.

Use the following guidelines when determining units:

• Identify the output variable of the rate (such as distance, volume, mass, or population).

• Identify the input variable with respect to which the rate is measured (such as time, position, or temperature).

• Combine these units as

  • (units of output per unit of input) × (units of input)

• Cancel matching units so that the final unit expresses the total amount of the output quantity accumulated.

Each of these steps reinforces the idea that accumulated change is an interpretation of area that intrinsically reflects the context of the rate and the domain.

The Role of the Independent Variable

The independent variable plays a critical role because it provides the dimension across which accumulation occurs. When the independent variable changes, even if the rate remains the same, the units of accumulated change adjust proportionally.

A normal sentence follows here to maintain required spacing before any equation or definition block appears again.

Interpreting Accumulated Change in Context

Correct unit interpretation is essential when describing changes in real-world systems. Because the accumulated change measures a total quantity, its units tell you exactly what has increased or decreased. Units guide interpretation in several ways:

• They indicate what quantity is being accumulated (e.g., miles, gallons, dollars).

• They reveal how the quantity changes over the interval (e.g., total distance traveled, total water added, total cost accrued).

• They clarify the relationship between rate and accumulation by showing how instantaneous behavior aggregates over time or another dimension.

• They prevent conceptual mistakes, such as confusing the rate itself with the accumulated amount.

Units as a Tool for Verification

Using units provides a powerful method for checking whether interpretations of area make sense. When evaluating the meaning of an integral of a rate function:

• Ensure that the resulting units correspond to a total amount, not a rate.

• Compare the units of the integrand and the variable of integration to confirm that the product produces an appropriate, contextually meaningful quantity.

• Use the units to verify whether graphical or numerical approximations of accumulated change reflect the intended physical interpretation.

This attention to units ensures consistency when applying integration to real-world problems and reinforces the conceptual meaning of accumulation in AP Calculus AB.