Completing the square is a powerful algebraic method that rewrites quadratic expressions in a form that exposes structure, allowing certain integrals to be evaluated using standard antiderivative formulas.

Completing the Square in the Context of Integration

In integration, completing the square is used to rewrite a quadratic expression so that it resembles forms whose antiderivatives are already known. This technique is especially useful when a quadratic appears inside a rational integrand or under a radical, and the expression is not easily factored or simplified in its original form. By reorganizing the quadratic into a perfect square plus or minus a constant, the integrand can often be matched to familiar patterns involving inverse trigonometric functions, logarithmic expressions, or basic substitution methods.

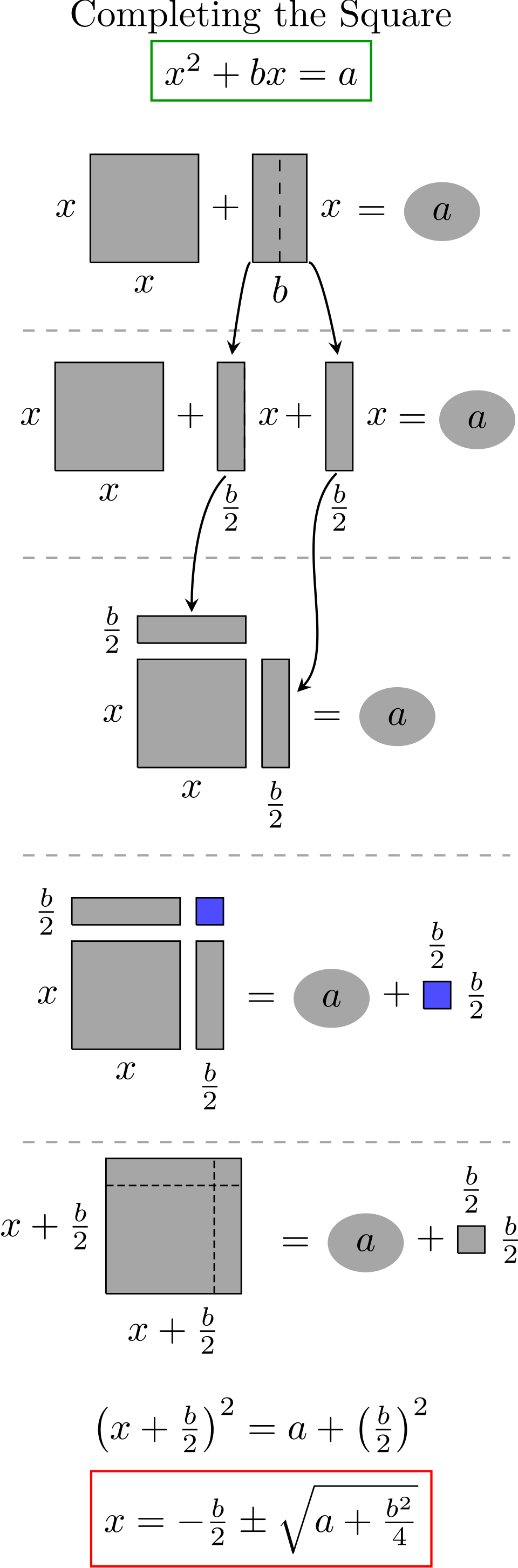
Geometric interpretation of completing the square, where the area represented by $x^2$ and the area represented by $bx$ are rearranged into a nearly complete square with a missing corner. Adding a small square of side $b/2$ completes the larger square, corresponding algebraically to adding $(b/2)^2$ to the expression. This image includes only the geometric motivation and does not show integration, which is addressed separately in the text. Source.

Why Completing the Square Matters

AP Calculus AB emphasizes fluency with fundamental integration techniques, and completing the square enables integrals to fit into standard templates. Many integrals involving expressions such as $ax^2+bx+c$ cannot be solved efficiently without rewriting them. When used effectively, this method transforms integrals into recognizable forms that allow direct or substitution-based evaluation. This makes completing the square an essential strategy for handling otherwise resistant quadratic expressions.

Structure of Quadratics and Perfect Squares

When working with an expression containing a quadratic, such as $ax^2+bx+c$, the first goal is to understand its structure. The technique uses algebraic manipulation to produce an expression of the form $a(x-h)^2+k$, known as vertex form.

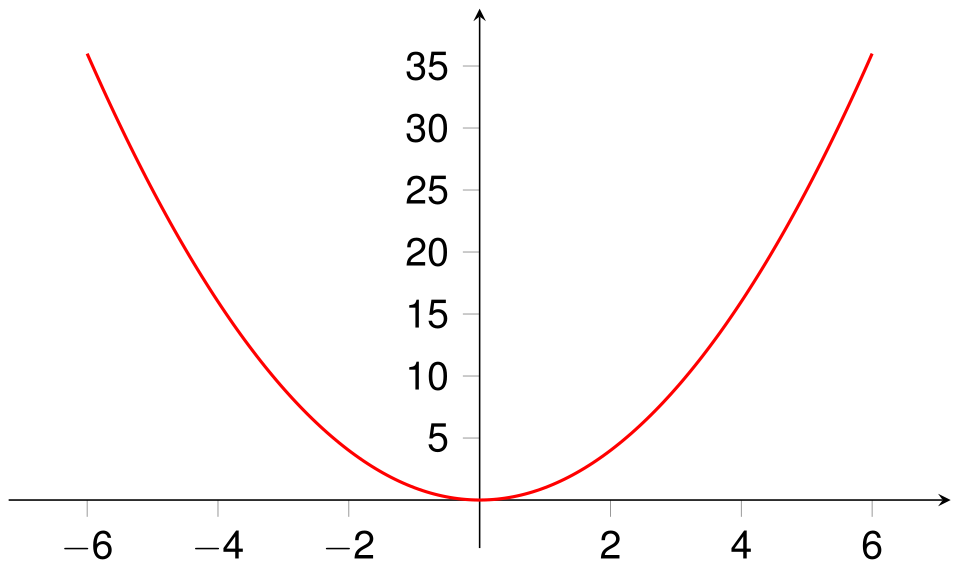
Graph of the basic quadratic function $y = x^2$, showing a parabola opening upward with its vertex at the origin. In vertex form, this would be written as $y = 1(x-0)^2 + 0$, illustrating how the parameters $h$ and $k$ in $a(x-h)^2+k$ correspond to horizontal and vertical shifts of the parabola. The image does not depict integration directly, but it clarifies how completing the square exposes the underlying quadratic structure used before applying integral formulas. Source.

After rewriting a quadratic as a perfect square plus a constant, the new form typically fits one of several recognizable integrand patterns.

When Completing the Square is Appropriate

Completing the square is most valuable when the quadratic appears:

• In the denominator of a rational expression.

• Under a square root where direct factoring is impractical.

• In an integrand that resembles inverse trigonometric derivative patterns.

• In any situation where rewriting the quadratic yields a simpler substitution.

These situations frequently appear in AP Calculus AB, especially when preparing an integrand for substitutions such as $u=x-h$ or for matching functions like the derivative of $\arctan(x)$.

Standard Forms Enabled by Completing the Square

Once a quadratic is rewritten as $a(x-h)^2+k$, it can resemble forms such as:

• $(x-h)^2+a^2$

• $a^2-(x-h)^2$

• $(x-h)^2-a^2$

These forms correspond to integration strategies involving inverse tangent, inverse sine, or logarithmic rules. The AP syllabus expects students to recognize and process these connections efficiently.

A sentence bridging to the next concept is necessary before any additional definition or equation block.

The Process of Completing the Square

To apply this technique correctly, the algebraic steps must be executed with precision:

Step-by-Step Structure

• Factor out the leading coefficient $a$ from the quadratic if $a \ne 1$.

• Identify the coefficient of $x$, divide it by 2, and square the result.

• Add and subtract this squared term inside the expression to maintain equality.

• Rewrite the trinomial portion as a perfect square.

• Combine constants to produce the final transformed quadratic.

• Reinsert factored constants if they were removed initially.

These steps yield an expression ideal for pairing with substitution.

Common Integration Patterns That Arise

After completing the square, students often encounter integrands structured like:

• A rational function resembling $1/(u^2+a^2)$

• A radical function resembling $\sqrt{a^2-u^2}$

• An integrand requiring a proportional $u$-substitution after completing the square

Such forms are central to AP Calculus AB and emphasize recognizing when algebra precedes calculus.

Strategic Insights for AP Calculus AB Students

Completing the square must be viewed not as an isolated algebra skill but as an integration strategy. Its purpose is to reveal hidden structure that matches known antiderivative patterns. Students should look for indicators such as:

• Quadratics that do not factor cleanly

• Integrals reminiscent of inverse trigonometric derivatives

• Rational expressions where direct substitution is impossible

• Radicals of quadratic expressions that are not already perfect squares

By converting the quadratic into a perfect square form, the integrand becomes compatible with substitution or direct antiderivative rules.

This method also allows students to recognize when integrals that seem complex are, in fact, manageable with proper algebraic rewriting. Completing the square transforms a challenging expression into one that clearly aligns with established integration formulas, reinforcing a connection between algebraic structure and calculus technique.