Selecting effective algebraic techniques helps transform difficult integrands into manageable forms, allowing standard integration methods to be applied efficiently and accurately within AP Calculus AB contexts.

Choosing Algebraic Techniques for Integration

This subsubtopic focuses on deciding which algebraic rearrangement best prepares an integrand for known antiderivative formulas. Because many expressions resist direct integration, strategically rewriting them often reveals the underlying structure needed for substitution, recognition of patterns, or application of familiar rules.

The Purpose of Algebraic Rearrangement

When an integrand appears complicated, the goal is to rewrite it into a more recognizable or standard form. This step improves clarity and makes subsequent techniques—such as basic antiderivative rules, $u$-substitution, or recognizing inverse trigonometric structures—more accessible. The choice of method depends on the type of expression, degree comparisons in rational functions, and whether quadratic expressions can be simplified.

When Long Division Is Appropriate

For rational functions of the form $\frac{P(x)}{Q(x)}$, determining whether the degree of the numerator is at least as large as the degree of the denominator is essential. If this occurs, polynomial long division is a natural first step. It rewrites a rational expression as a polynomial plus a proper fraction.

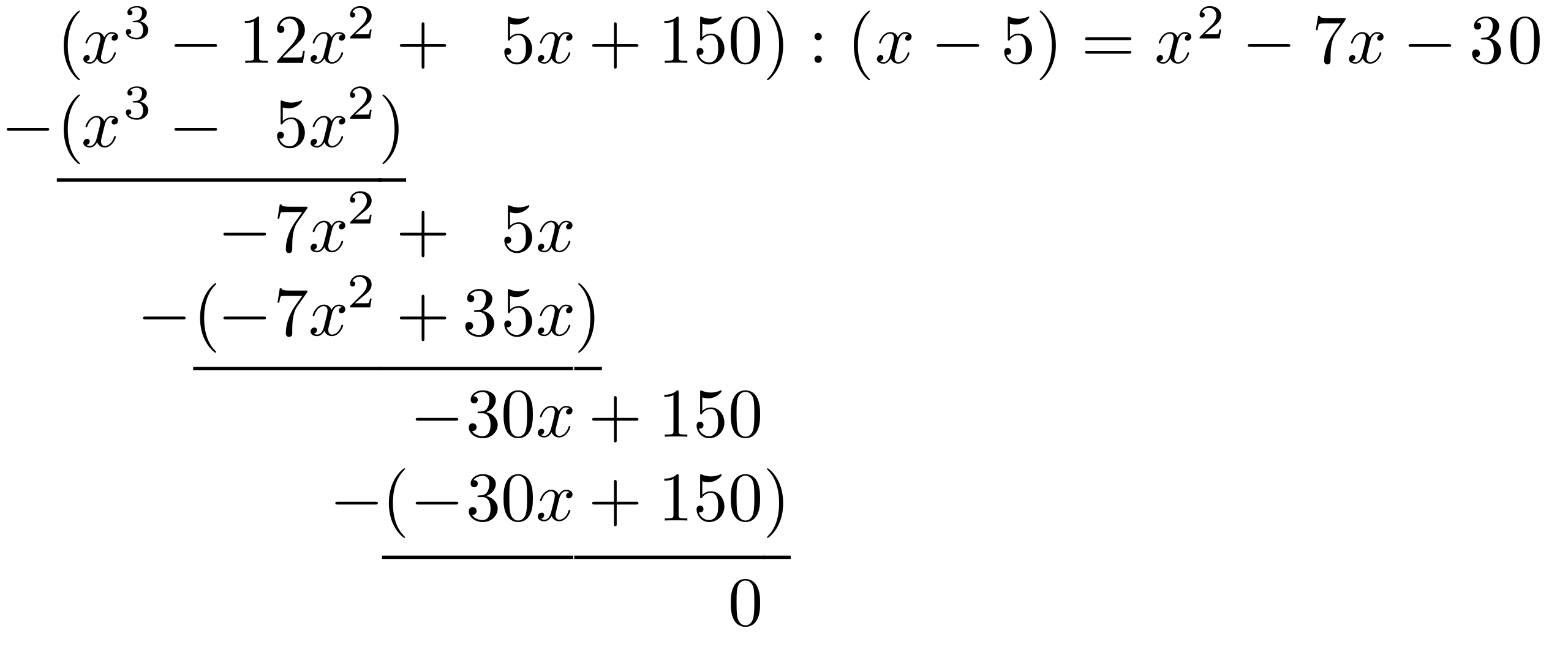
This diagram illustrates polynomial long division applied to a specific example, showing how a rational expression is decomposed into a polynomial plus a remainder term. The structure reinforces the idea that long division is used when the numerator’s degree is at least as large as the denominator’s degree. The specific numbers present exceed the syllabus’s generality but simply instantiate the same algebraic technique. Source.

Once rewritten, the polynomial part is integrated directly, while the remaining rational expression often aligns with $u$-substitution or logarithmic forms. This makes long division an initial checkpoint whenever confronting high-degree numerators.

When Completing the Square Is Appropriate

Quadratic expressions in the denominator or inside radicals often benefit from completing the square, which rewrites the quadratic in a structured, centered form. This technique is valuable because many integrals rely on recognizing patterns involving $(x - h)^2 + k$. These patterns connect directly to antiderivatives involving logarithmic or inverse trigonometric functions.

After completing the square, the integrand may simplify into a form suitable for substitution that directly reveals standard integral results.

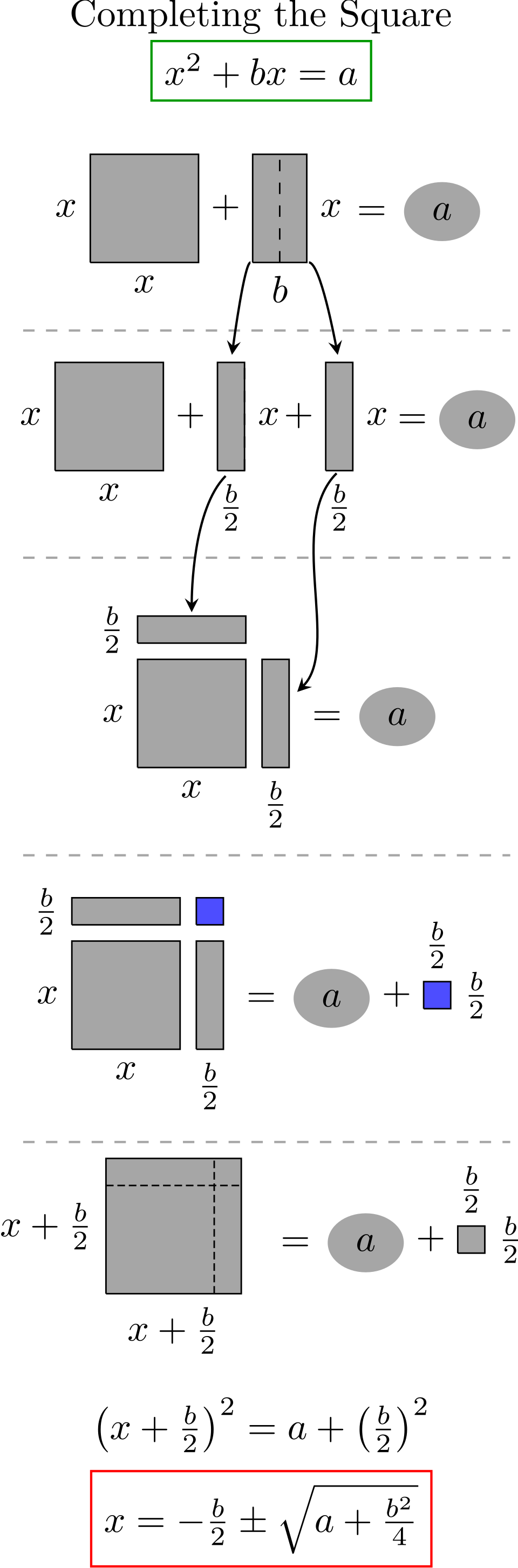
This geometric figure shows how the expression $x^2 + bx$ can be completed into a full square by adding a smaller square of side $b/2$. The visual reinforces the algebraic idea that completing the square rewrites a quadratic into the form $(x-h)^2 + k$, making its structure easier to work with. The geometric viewpoint goes slightly beyond syllabus requirements but deepens understanding of the same algebraic method. Source.

Distinguishing Integrands to Select a Technique

Determining whether to use long division or completing the square requires identifying the algebraic features of the integrand. Students should look for cues that indicate how the expression can be simplified.

• Use long division when:

  • The numerator’s degree is greater than or equal to the denominator’s degree.

  • A rational function is difficult to decompose or interpret as written.

  • Simplifying to a proper fraction makes the remaining structure recognizable.

• Use completing the square when:

  • A quadratic expression appears in a denominator or radical.

  • The structure resembles known inverse trigonometric derivative forms.

  • Transforming the expression reveals symmetry that assists substitution.

Normal integrands often require evaluating whether they align with standard formulas before deciding to attempt further substitution. The goal is always to simplify the form, not to increase complexity.

Recognizing Patterns That Guide Technique Selection

A significant part of selecting an algebraic technique involves visual familiarity with common integrable structures. Because many integration rules rely on identifying these patterns, algebraic manipulation is used to transform an unfamiliar integrand into one that fits a known model.

Key patterns to observe include:

• Quadratic expressions that are nearly perfect squares.

• Degree relationships in rational functions.

• Symmetry in expressions such as $x^2 + 4x + 7$ that become cleaner after completion.

• Rational expressions where the numerator resembles the derivative of the denominator, suggesting substitution.

How Algebraic Techniques Support Other Integration Methods

An important purpose of the techniques in this subsubtopic is not to complete the integral themselves but to prepare the integrand for another method.

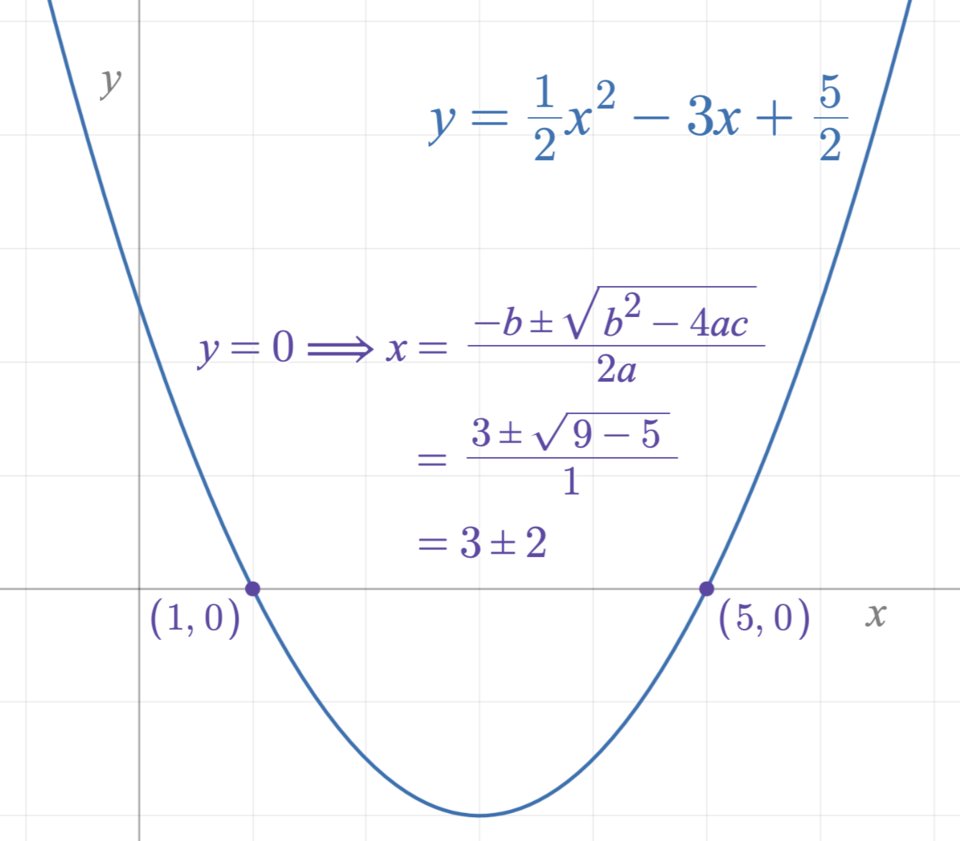
This derivation shows how starting from $ax^2 + bx + c = 0$, completing the square leads to isolation of $x$ and ultimately the quadratic formula. It demonstrates a full sequence of algebraic rearrangements paralleling how integrands are rewritten before applying standard integration techniques. The explicit root formula is additional material but the intermediate steps align directly with the algebraic decision-making emphasized in this subsubtopic. Source.

Once rewritten, the expression may clearly indicate how to proceed with integration.

For example:

• Simplifying via long division may reveal a logarithmic structure in the remaining fraction.

• Completing the square may convert an obscure rational expression into a clear inverse trigonometric form.

• Rewriting may expose the derivative of an inner function, making $u$-substitution straightforward.

These transformations support efficient problem solving and ensure students avoid unnecessary or overly complex approaches.

Practical Strategy for AP Calculus AB Students

When approaching any challenging integrand, students should follow a decision process to determine whether algebraic rearrangement is necessary.

• Scan for degree relationships in rational functions.

• Examine quadratics in denominators or radicals for potential square completion.

• Identify whether substitution patterns already exist, avoiding unnecessary manipulation.

• Choose the simplest algebraic technique that reveals a standard form.

• Rewrite only what is required to expose the integrand’s structure.

This systematic approach aligns with the syllabus requirement to select and use appropriate algebraic rearrangements that lead to integrable forms.