AP Syllabus focus:
‘Rewrite certain rational functions using polynomial long division so that standard antiderivative formulas or substitution methods can be applied more easily.’
Using algebraic long division allows integrals of complicated rational functions to be rewritten into simpler expressions, enabling AP Calculus AB students to apply familiar antiderivative rules effectively.
Using Algebraic Long Division Before Integrating
Algebraic long division is a valuable tool when integrating rational functions, which are expressions written as one polynomial divided by another. When the degree of the numerator is greater than or equal to the degree of the denominator, direct integration using basic rules is often impossible. In these situations, polynomial long division rewrites the integrand into simpler components, making integration manageable using known techniques.
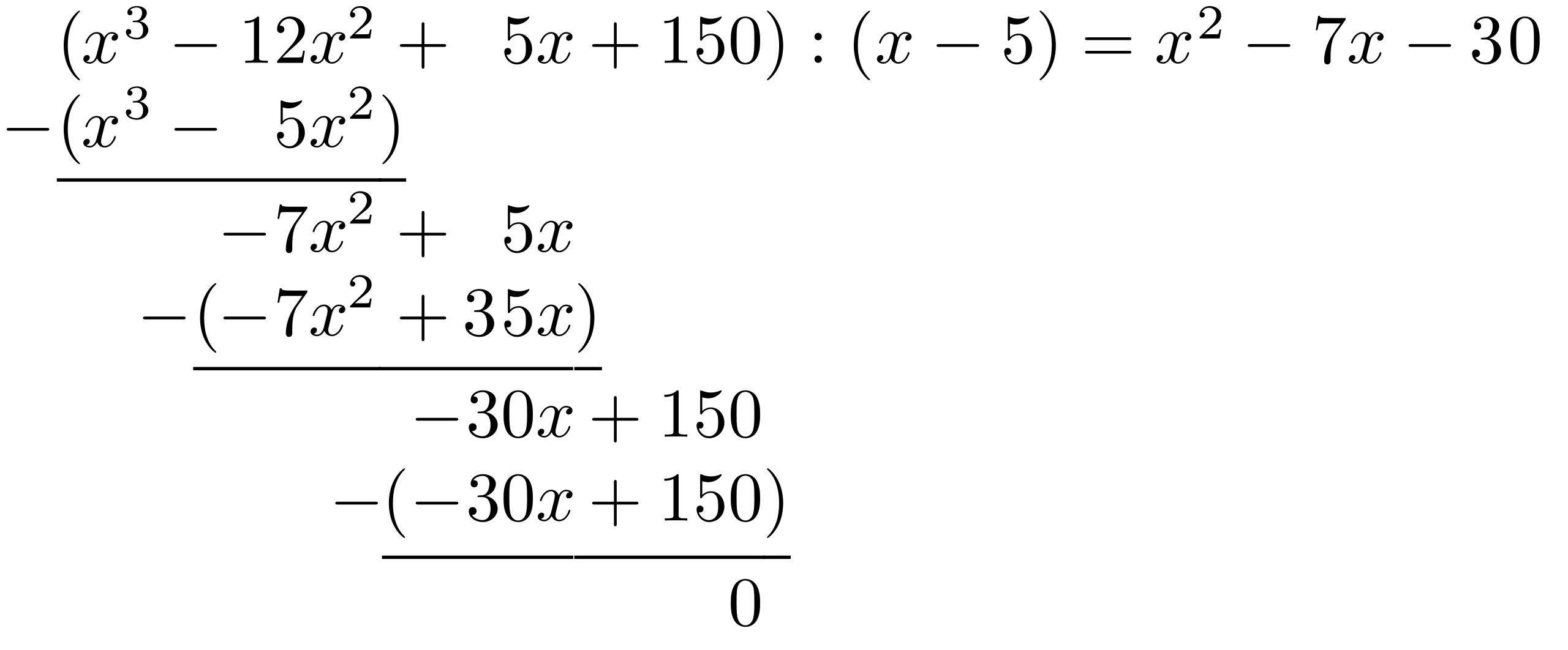
A worked example of polynomial long division arranged in the standard bracket format. The structure highlights how each dividend term is matched with a divisor term to produce the quotient and remainder. The specific polynomials shown are illustrative only and not tied to any AP Calculus AB problem. Source.
When Long Division Is Necessary
A rational function becomes difficult to integrate directly if the numerator’s polynomial degree is too large relative to the denominator. Long division transforms such expressions into a combination of:
A polynomial expression that is straightforward to integrate.
A proper fraction whose numerator has a lower degree than its denominator.
A remainder term that may be suitable for substitution or other basic antiderivative rules.
This process ensures that standard integration formulas can be applied without unnecessary algebraic complexity. It aligns directly with the syllabus requirement to “rewrite certain rational functions using polynomial long division so that standard antiderivative formulas or substitution methods can be applied more easily.”
Identifying Rational Functions Requiring Long Division
AP Calculus AB students should recognize when polynomial long division is appropriate. The key indicator is the relationship between the degrees of the numerator and denominator:
If degree of numerator ≥ degree of denominator, division is required before attempting integration.
If degree of numerator < degree of denominator, no division is needed, and other techniques may be used.
This identification step guides the integration strategy and prevents improper application of substitution or other methods when the integrand can be simplified first.
Structure of a Rational Function After Long Division
Long division rewrites a rational function into a more integrable form. The general structure becomes:
A polynomial term that integrates using power rules.
A proper rational expression where substitution may apply.
A remainder term that simplifies the integration process.
= Quotient polynomial
= Remainder polynomial
= Divisor polynomial
A normal sentence must appear between equation or definition blocks to follow the formatting requirements, and that purpose is served here by reinforcing the usefulness of algebraic restructuring.
After division, the integrand becomes a sum of manageable pieces rather than a single complicated fraction.
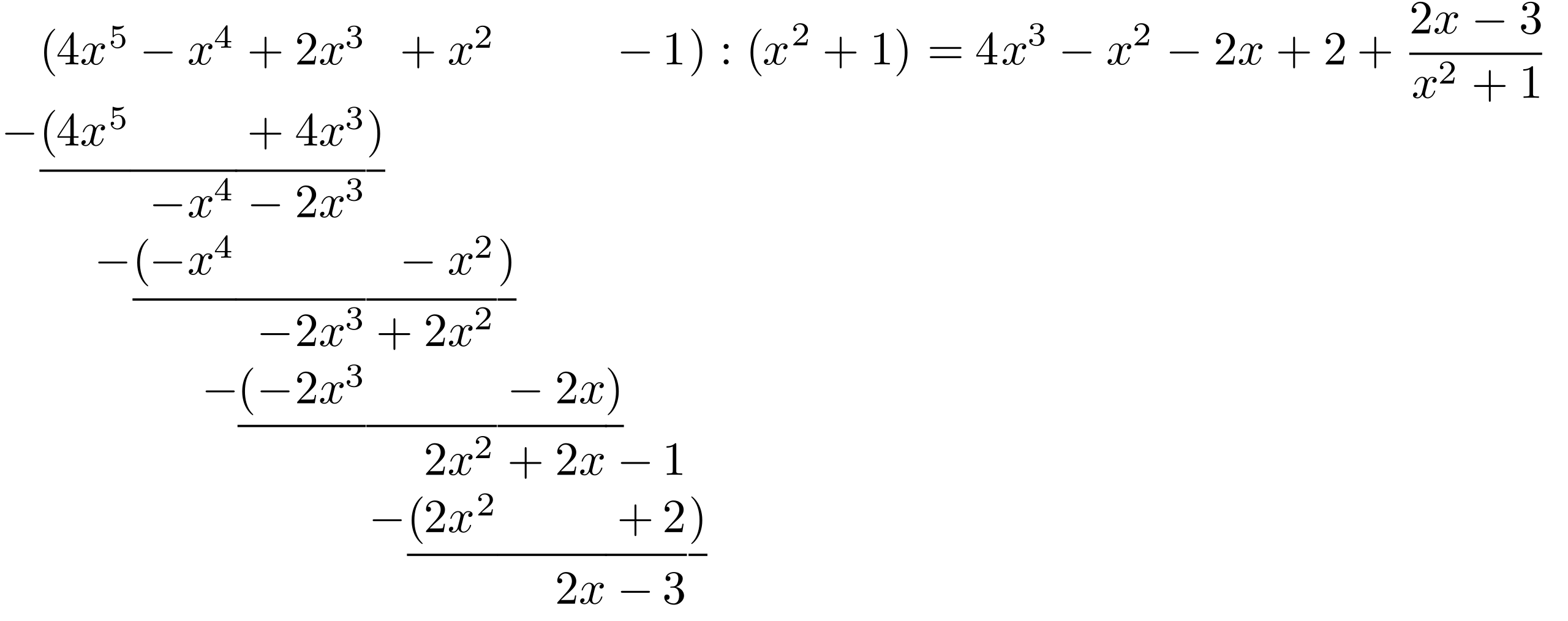
Polynomial long division with a quadratic divisor shows how an improper rational function can be decomposed into a polynomial plus a proper fractional remainder. This layout emphasizes aligning like powers and subtracting carefully at each step. The expressions displayed are specific to this example and serve only to illustrate the general method. Source.
Key Terms Related to Polynomial Long Division
When this technique appears in integration contexts, students must understand the terminology used to describe the parts of the divided expression.
Proper Rational Function: A rational function whose numerator has lower degree than its denominator.
A proper rational function is easier to integrate and often leads directly to substitution or recognition of derivative-in-the-numerator patterns.
Long division complements other algebraic techniques by providing a first step when dealing with improper rational functions. This early simplification also prevents unnecessarily complex antiderivative methods.
Process Overview for Using Long Division Before Integrating
To apply polynomial long division effectively in an integration context, students should follow a structured approach. Each step aligns with strategies used throughout the AP Calculus AB course.
Check polynomial degrees
Determine whether division is necessary by comparing the degrees of the numerator and denominator.Apply polynomial long division
Rewrite the rational function into a quotient plus a proper fraction.Separate the integrand
Express the resulting function as a sum of simpler terms suitable for standard integration formulas.Identify which antiderivative rules apply
The quotient integrates using power rules, while the remaining fraction may use substitution or recognized derivative forms.Integrate each term individually
Proceed one component at a time, maintaining structured mathematical reasoning.
Why Long Division Enhances Integrability
This graph illustrates the type of rational functions that may require simplification before applying antiderivative techniques.
A rational function becomes difficult to integrate directly if the numerator’s polynomial degree is too large relative to the denominator.
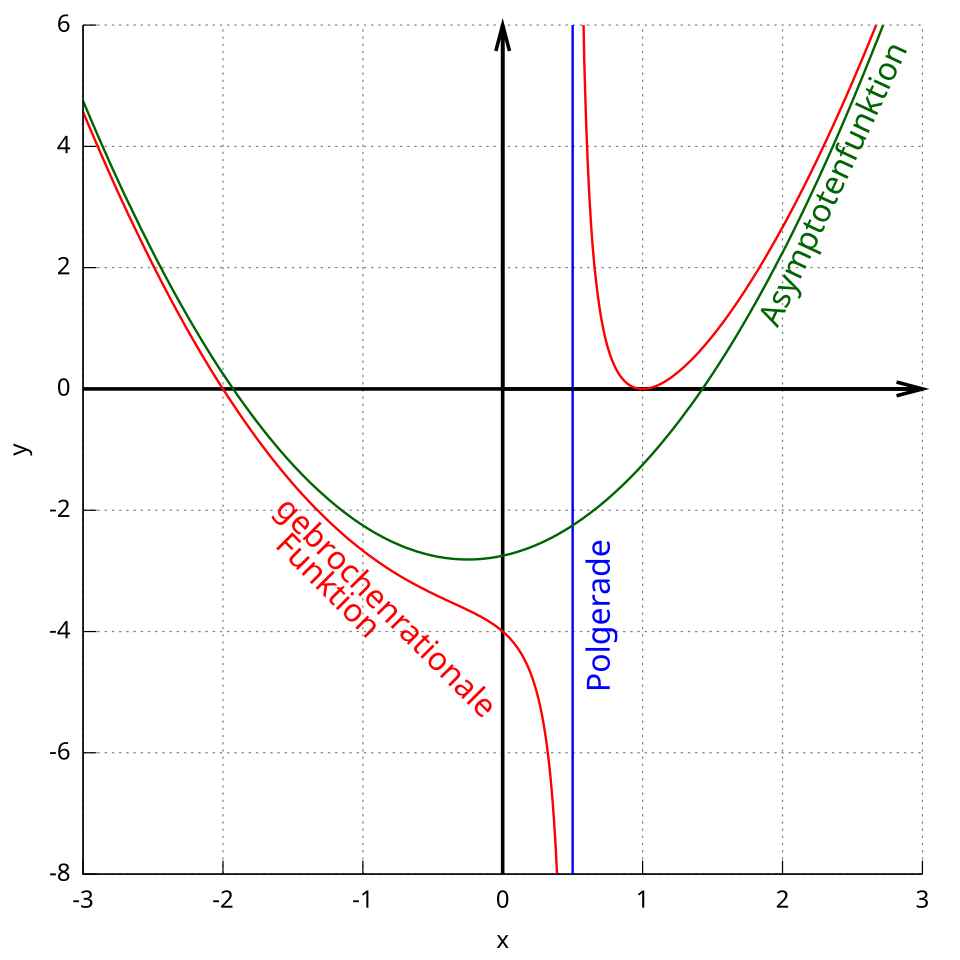
A graph of a rational function shows typical features such as vertical asymptotes and long-term asymptotic behavior. These features help illustrate why improper rational functions often benefit from algebraic simplification before integration. The asymptote values and curve shown belong to this specific example and include extra analytic detail not required by the syllabus. Source.
Long division supports AP Calculus AB goals by transforming challenging rational expressions into accessible forms that align with the key themes of antidifferentiation. It simplifies integrands to match basic rules, clarifies when substitution can be applied, and reduces algebraic obstacles so that standard calculus procedures can proceed effectively.
FAQ
Check the structure of the rational function before considering any other technique.
If the numerator’s degree is equal to or greater than the denominator’s degree, long division must be applied first to reduce the expression to a proper rational form.
Other algebraic methods only become useful after the integrand has been simplified and no longer requires division.
Long division rewrites the integrand into an equivalent expression without altering its underlying function. The decomposition into quotient and remainder is an algebraic identity.
Since integration depends solely on the function’s values, not the form in which it is written, the integral remains exactly the same.
Division continues until the leftover polynomial cannot be divided further by the divisor.
This ensures the remainder is of strictly lower degree, creating a proper rational expression. Proper rational functions are easier to integrate because they often resemble standard derivative–antiderivative pairs.
Common mistakes include:
• Misaligning terms when subtracting intermediate results
• Introducing sign errors when distributing subtraction
• Forgetting to write all powers of x in descending order, even if a coefficient is zero
To avoid these, rewrite both polynomials in full descending-power form and check each subtraction step carefully.
Synthetic division can be useful, but only when the divisor is linear and written in the form x − a.
If the divisor is quadratic or higher, synthetic division cannot be applied, and full long division must be used.
Even when synthetic division works, it may be less transparent for integration purposes because long division makes the quotient–remainder structure clearer for rewriting the integrand.
Practice Questions
Question 1 (1–3 marks)
The function f(x) = (3x^3 + 2x^2 – 5x + 4) / (x^2 – 1) is to be integrated.
(a) Explain why polynomial long division is required before attempting to integrate f(x).
(b) State the degree of the numerator and denominator to support your answer.
Question 1
(a) 1 mark for stating that the numerator has higher degree than the denominator, making the expression improper.
(b) 1 mark for identifying degree of numerator = 3.
1 mark for identifying degree of denominator = 2.
Question 2 (4–6 marks)
Consider the rational function g(x) = (2x^3 – 7x + 5) / (x^2 + 2).
(a) Perform polynomial long division to rewrite g(x) in the form Q(x) + R(x)/(x^2 + 2), where Q(x) is a polynomial and R(x) is a remainder polynomial.
(b) Hence state the form of the integral of g(x) with respect to x, without evaluating the integral.
(c) Briefly explain why this rewritten form is more suitable for applying standard integration techniques.
Question 2
(a) 1 mark for correctly dividing to obtain a linear quotient.
1 mark for correctly determining the remainder polynomial.
1 mark for expressing the function in the required Q(x) + R(x)/(x^2 + 2) form.
(b) 1 mark for stating that the integral becomes the integral of the quotient plus the integral of the remainder term divided by (x^2 + 2).
(c) 1–2 marks for correctly explaining that the quotient can be integrated directly using basic rules, while the remainder term is a proper rational expression suitable for substitution or known formulas.

