Using Limits to Evaluate Improper Integrals (6.13.2) | AP Calculus AB Notes

AP Syllabus focus:
‘Rewrite an improper integral as a limit of definite integrals and evaluate the limit, when it exists, to determine the value of the integral.’

Improper integrals arise when an interval is unbounded or the integrand becomes unbounded, and limits provide a rigorous method for determining whether these integrals produce meaningful accumulated values.

Understanding Improper Integrals

Improper integrals appear in two main situations: when the interval of integration is infinite or when the integrand becomes unbounded within the interval. Because traditional definite integrals require a finite interval and a continuous integrand, these special cases require an extended approach based on limits.

Improper Integral: An integral in which the interval of integration is infinite, or the integrand is unbounded at one or more points of the interval.

Improper integrals help quantify accumulated change in contexts where growth continues indefinitely or where a rate becomes extremely large near specific points. For AP Calculus AB, the focus is on understanding how limits transform these undefined expressions into well-defined values when they converge.

Using Limits to Define Improper Integrals over Infinite Intervals

When the interval extends to infinity, a definite integral cannot be evaluated directly. Instead, the integral is replaced by a limit with a finite bound that grows without bound.

$\int_{a}^{\infty} f(x),dx = \lim_{b \to \infty} \int_{a}^{b} f(x),dx$
$a$ = Lower limit of integration, a real number
$b$ = Temporary upper limit approaching infinity

A normal sentence must occur before another block. Using limits in this way ensures the accumulation is evaluated only after verifying whether the total area approaches a finite value.

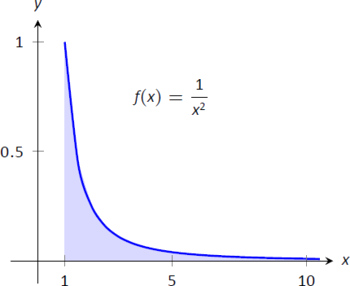
Graph of $f(x)=1/(1+x^2)$ on $[0,\infty)$ with the region under the curve shaded as the upper bound increases, illustrating how an improper integral over an infinite interval is defined using a limit. The panels demonstrate that as $b$ grows, the accumulated area approaches a finite value. The specific function is an example beyond the syllabus but clearly reinforces the limit-based definition. Source.

$\int_{-\infty}^{a} f(x),dx = \lim_{b \to -\infty} \int_{b}^{a} f(x),dx$
$a$ = Upper finite limit
$b$ = Temporary lower limit approaching negative infinity

These forms allow students to reinterpret areas over infinite regions as predictable limits of growing intervals.

Using Limits for Vertical Asymptotes or Unbounded Integrands

A second situation occurs when the integrand becomes unbounded at an endpoint or within the interval. This typically happens when the function has a vertical asymptote, meaning it increases or decreases without bound near a specific value of $x$ .

Vertical Asymptote: A value of the independent variable where a function increases or decreases without bound.

When the asymptote occurs at an endpoint, the integral is rewritten so the problematic bound is approached using a limit.

$\int_{a}^{b} f(x),dx = \lim_{t \to a^{+}} \int_{t}^{b} f(x),dx$
$a$ = Endpoint where the integrand is unbounded
$b$ = Upper finite limit
$t$ = Temporary limit approaching $a$ from the right

A normal sentence must separate any two equation or definition blocks. This method ensures the accumulation is computed only if the limit exists as the integrand grows without bound.

$\int_{a}^{b} f(x),dx = \lim_{t \to b^{-}} \int_{a}^{t} f(x),dx$
$a$ = Lower finite limit
$b$ = Endpoint where the integrand is unbounded
$t$ = Temporary limit approaching $b$ from the left

If $f$ is unbounded at an interior point $c$ of $(a,b)$ , we split the integral at $c$ and use separate one-sided limits on $[a,c)$ and $(c,b]$ .

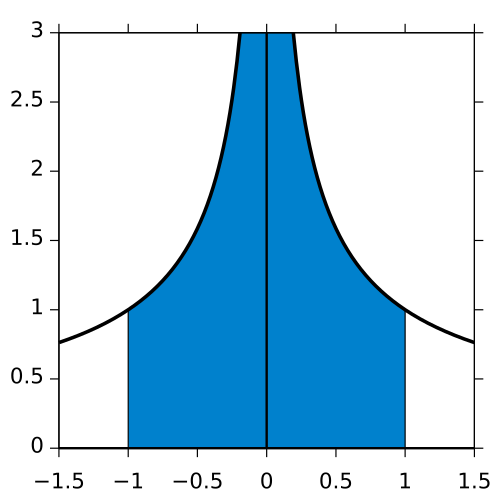
Graph of $f(x)=1/\sqrt[3]{x^2}$ on $[-1,1]$ with the region around the vertical asymptote at $x=0$ shaded to show an improper integral unbounded at an interior point. The picture illustrates how the interval is split and each side evaluated using separate limits. The specific function and numerical value shown exceed syllabus requirements but visually support the concept effectively. Source.

Convergence and Divergence

The limit used to define an improper integral may or may not produce a finite value. The integral is considered convergent when the limit approaches a real number and divergent when the limit fails to exist or becomes infinite.

Convergence: The behavior of an improper integral when its defining limit approaches a finite real number.

Students must pay close attention to the existence and value of the limit because the final numerical result depends entirely on whether the accumulation stabilizes.

A key insight for AP Calculus AB is that convergence and divergence describe behavior rather than computation strategy. This means the limit itself determines whether the accumulated change is meaningful. If the limit is infinite or undefined, the improper integral does not produce a finite area.

Steps for Using Limits to Evaluate Improper Integrals

Students can apply a consistent structure when rewriting and evaluating improper integrals:

Identify the source of improperness
Determine whether the issue is an infinite interval or an unbounded integrand.
Rewrite the integral using limits
Replace the problematic bound with a variable and express the integral as a limit of definite integrals.
Evaluate the definite integral first
Treat the temporary bound as a constant and compute the integral normally.
Apply the limit
Examine the resulting expression to determine whether it converges to a finite number or diverges.
Interpret the result
Understand whether the situation represents a meaningful total accumulation of change.

Importance within the AP Curriculum

Subsubtopic 6.13.2 emphasizes the need to connect integration and limits in a rigorous way. Because improper integrals break traditional assumptions about continuity and finite intervals, limits serve as the essential mathematical bridge. This connection reinforces earlier limit concepts and strengthens a student’s ability to reason about infinite processes and unbounded behavior in accumulation contexts.

FAQ

Rewriting the integral with a limit is necessary because the definite integral does not exist in its original form when the interval is infinite or the integrand is unbounded. The limit creates a valid mathematical definition that replaces the undefined integral.

Direct evaluation without using limits risks ignoring the behaviour of the function near the problematic bound. The limit formally checks whether the accumulated area actually settles to a finite value.

A useful approach is to compare the integrand with a known benchmark function whose convergence behaviour is established.

Common comparisons include:
• Functions resembling 1/x to a power for large x.
• Functions that grow or decay faster than known convergent or divergent forms.

If your function is always less than a known convergent benchmark for large x, it is likely to converge; if it is greater than a divergent benchmark, it is likely to diverge.

If the integrand has multiple problematic points, such as more than one place where it becomes unbounded, each requires its own limit.

Splitting at these points isolates the behaviour near each discontinuity.
If any resulting limit diverges, the entire improper integral diverges regardless of the other parts.

This ensures all parts of the integral are treated consistently and according to their behaviour.

Yes. Convergence depends on the rate at which the integrand grows, not merely on the fact that it grows.

For example, some functions increase sharply but only over a very small interval, causing the area to remain finite.
What matters is whether the total accumulation remains bounded when the limit is taken.

This illustrates that unboundedness alone does not determine divergence.

Many real-world models involve behaviours that extend indefinitely or feature rapid increases near certain points. Improper integrals allow these scenarios to be analysed using standard calculus.

Examples include:
• Modelling decay or growth processes over very long periods.
• Describing physical quantities near singularities, such as fields near point charges.

Using limits ensures that the accumulated quantity is meaningful and mathematically justified when interpreting results.

Practice Questions

Consider the improper integral from 1 to infinity of 2 divided by x squared.
(a) Write this integral as a limit of definite integrals.
(b) Determine whether the integral converges or diverges.
[3 marks]

(a) Correct limit expression:
Integral from 1 to infinity of 2/x^2 dx = limit as b approaches infinity of the integral from 1 to b of 2/x^2 dx.
1 mark

(b) Correct evaluation of the limit or correct conclusion of convergence:
Integral evaluates to 2.
1 mark
Correct justification that the area approaches a finite value as b increases.
1 mark

The function f is defined on the interval from 0 to 3 by f(x) = 1 divided by the square root of (3 minus x).
(a) Explain why the definite integral from 0 to 3 of f(x) dx is improper.
(b) Rewrite the integral as a limit.
(c) Evaluate the limit to determine the value of the integral.
(d) State whether the integral converges or diverges, giving a reason.
[6 marks]

(a) Correct explanation that f becomes unbounded as x approaches 3 from the left.
1 mark

(b) Correct limit form:
Integral from 0 to 3 of f(x) dx = limit as t approaches 3 from below of the integral from 0 to t of 1/sqrt(3 - x) dx.
1 mark

(c) Correct evaluation of the definite integral before taking the limit (e.g., substitution leading to an expression involving sqrt(3 - x)).
1 mark
Correct evaluation of the limit giving 2.
1 mark

(d) Correct conclusion that the improper integral converges, with reasoning.
1 mark

Try All Topic Practice Questions

Written by:

Dr Rahil Sachak-Patwa

Oxford University - PhD Mathematics

Rahil spent ten years working as private tutor, teaching students for GCSEs, A-Levels, and university admissions. During his PhD he published papers on modelling infectious disease epidemics and was a tutor to undergraduate and masters students for mathematics courses.