Improper integrals arise when intervals are infinite or integrands are unbounded, making it essential to analyze their limiting behavior and determine whether they produce finite accumulated values.

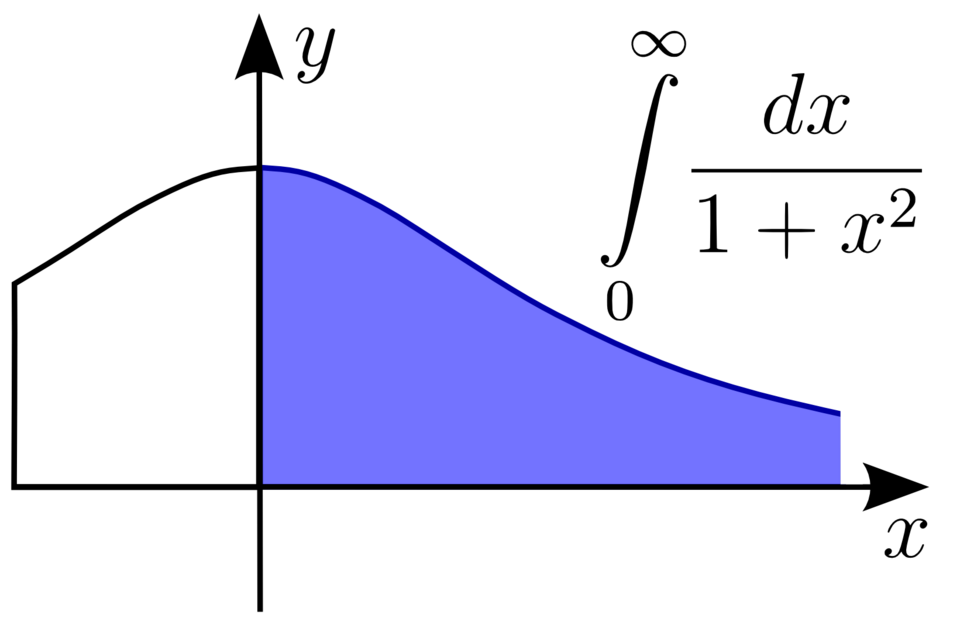
A graph of a positive, decreasing function on $[0,\infty)$ with the area under the curve shaded to represent an improper integral over an infinite interval. Even though the $x$-axis extends without bound, the total shaded area can converge to a finite value. The formula shown on the source page goes slightly beyond AP Calculus AB but reinforces the same convergence idea. Source.

Convergent and Divergent Improper Integrals

Understanding Improper Integrals

An improper integral is a definite integral in which either the interval of integration is infinite or the integrand becomes unbounded at one or more points within the interval. When the integral involves such behavior, traditional methods no longer apply directly, and the integral must be evaluated by examining its behavior as a limit. This aligns directly with the syllabus requirement to determine whether an improper integral converges (approaches a finite value) or diverges (fails to approach a finite value).

Improper integrals allow us to quantify total accumulated change even in situations where the interval extends indefinitely or where the function spikes toward infinity. To determine whether the accumulation remains finite, we rely on limit-based reasoning.

Why Convergence and Divergence Matter

Convergence indicates that, despite infinite extent or unbounded behavior, the rate of accumulation diminishes sufficiently to settle at a finite total. Divergence signals that the accumulated area grows without bound or fails to settle, meaning no finite value can represent the integral. This is essential when interpreting integrals in physical or applied contexts, such as total mass, energy, or probability.

Types of Improper Integrals Requiring Convergence Analysis

Improper integrals typically fall into two categories. In each scenario, determining convergence requires examining whether a limit exists.

• Infinite intervals of integration, such as

  • $\int_a^\infty f(x),dx$

  • $\int_{-\infty}^b f(x),dx$

  • $\int_{-\infty}^\infty f(x),dx$

• Integrands with vertical asymptotes, such as

  • $\int_a^b f(x),dx$ where $f(x)$ is unbounded at $a$, $b$, or at some point in $(a,b)$.

After identifying the type, the behavior of associated limit expressions determines convergence.

Limit-Based Reformulation of Improper Integrals

Improper integrals are defined using limits that approach the problematic value—either infinity or a point of discontinuity. The following structure is essential for establishing convergence and divergence for AP Calculus AB.

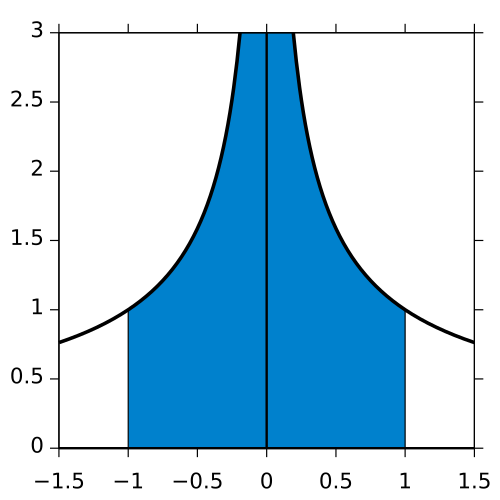
A graph of a function with a vertical asymptote at $x=0$ and the area shaded between $x=-1$ and $x=1$, illustrating an improper integral unbounded at an interior point. The shaded region demonstrates that although the function spikes near the asymptote, the total area can converge when defined through one-sided limits. The equation shown on the source page exceeds AP Calculus AB requirements but supports the same conceptual reasoning about convergence. Source.

A single limit is sufficient when only one part of the interval is improper. When both limits are improper, limits are taken separately and evaluated independently.

A sentence must follow before placing another definition or equation block, ensuring clarity and separation of conceptual ideas for the learner.

Convergence Criteria

To decide whether an improper integral converges, the key is to compute or analyze the resulting limit expression. The entire integral converges only when the limit exists and yields a finite real number. If the limit fails to exist or grows without bound, the integral diverges.

Useful indicators for convergence include the following:

• Magnitude of the integrand: Functions that decrease sufficiently fast (for example, reciprocals of high powers of $x$) are more likely to converge.

• Behavior near vertical asymptotes: The sharpness of the spike in the function determines whether accumulated area becomes infinite.

• Comparison to known benchmark functions: In more advanced practice, students compare an integrand with a simpler function whose convergence behavior is known.

Divergence Criteria

An improper integral diverges when its limit grows without bound, oscillates without settling to a finite value, or is undefined. Divergence indicates that the total accumulated area under the function cannot be expressed as a finite quantity.

Common indicators of divergence include:

• Slow decay on infinite intervals

• Extreme unbounded growth near discontinuities

• Oscillatory behavior without diminishing amplitude (though AP Calculus AB rarely tests oscillatory divergence explicitly)

Procedures for Determining Convergence or Divergence

Students should adopt a consistent approach when analyzing improper integrals.

• Identify why the integral is improper: infinite interval or unbounded integrand.

• Rewrite the integral using limits appropriate to the situation.

• Evaluate the resulting limit, either analytically or with supporting reasoning.

• Determine whether the limit exists and is finite.

• Conclude convergence when the limit yields a real number and divergence when it does not.

Graphical and Conceptual Interpretation

Understanding convergence also benefits from interpreting functions graphically. A function whose area tapers off toward zero over an infinite interval may still yield a finite total accumulation. Conversely, a function that grows too quickly near an asymptote produces infinitely large areas. Conceptualizing “area accumulation behavior” supports recognition of convergence patterns even before formal calculation.

Importance for Accumulation and Applications

Deciding whether an improper integral converges ensures meaningful interpretation of accumulated quantities, particularly when modeling phenomena such as decay, infinite processes, or rates exhibiting vertical asymptotes. In all cases, the limit structure is the central tool for judging whether total accumulation stabilizes or becomes unbounded.

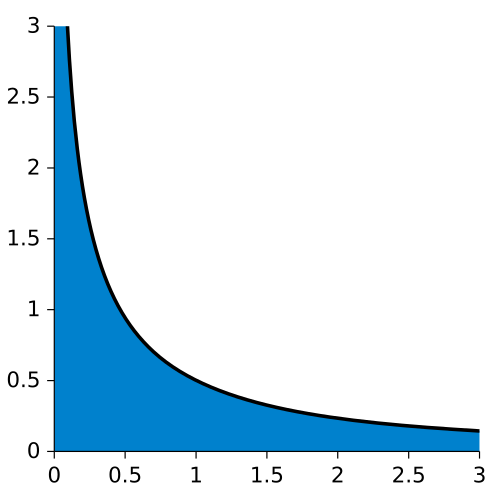
A graph of a function unbounded near $x=0$ and decreasing over an infinite interval, with the area under the curve shaded to represent an improper integral. The integral shown on the source page, such as $\int_{0}^{\infty} \frac{dx}{(x+1)\sqrt{x}}$, is improper both because of the infinite interval and the unbounded behavior at zero, yet it converges to a finite value. The detailed expression extends beyond AP Calculus AB but illustrates the role of limits in determining convergence. Source.