Improper integrals extend the concept of definite integrals to situations where boundaries or integrands behave atypically, allowing the accumulation of change to be analyzed beyond ordinary finite, well-behaved intervals.

Understanding the Nature of Improper Integrals

Improper integrals arise when a definite integral does not meet the usual requirements for standard evaluation. In the typical definite integral, a function is continuous on a closed, finite interval, and the integral computes the net accumulation across that interval. However, certain real-world and theoretical problems involve integrals whose domains extend infinitely or whose functions exhibit unbounded behavior within the interval of integration. These cases demand a broader conceptual framework.

When an integral includes infinite bounds or involves a function that becomes infinitely large near some point in the interval, it is classified as an improper integral. Recognizing such situations is essential before attempting any further evaluation or analysis.

Identifying Improper Integrals: Infinite Limits

Infinite Integration Bounds

One of the most direct indicators of an improper integral is the presence of infinite limits of integration. These occur when a definite integral extends toward positive or negative infinity rather than stopping at a finite boundary.

A sentence explaining this definition must follow. When a limit is infinite, the integral no longer measures area over a finite stretch of the real line, so it cannot be interpreted in the standard geometric sense.

Common scenarios involving infinite bounds include:

• Integrals of functions describing long-term behavior as time grows indefinitely.

• Integrals analyzing decay, growth, or distribution across an infinite domain.

• Any definite integral written with limits such as $[a, \infty)$, $(-\infty, b]$, or $(-\infty, \infty)$.

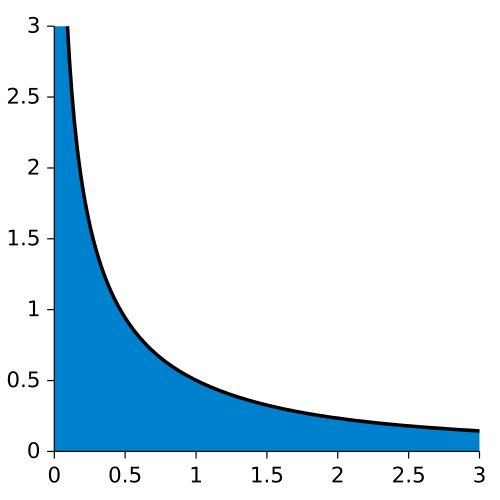
Graph of $y=\dfrac{1}{\sqrt{x}(x+1)}$ with the area under the curve shaded from a point near $x=0$ out toward large $x$, illustrating an improper integral whose domain is unbounded and whose integrand blows up near $x=0$. Both features show why this integral is improper even though the shaded region has a well-defined finite area. Some versions note that $\int_{0}^{\infty}\dfrac{1}{(x+1)\sqrt{x}},dx=\pi$, which is beyond the recognition focus of this subtopic. Source.

Characteristics of Infinite-Interval Problems

Integrals with infinite bounds often involve functions that may converge toward zero or oscillate as the variable increases without bound. Students must determine whether the integral makes sense as a measure of accumulated change across an unbounded interval.

Important traits to recognize include:

• The independent variable extends indefinitely.

• The domain is not closed or finite.

• The accumulation must be interpreted through limiting behavior.

Identifying Improper Integrals: Unbounded Integrands

Integrands with Vertical Asymptotes or Singularities

The second major category arises when the integrand becomes unbounded at some point in the interval. Even if both integration limits are finite, the integral can still be improper if the integrand grows without bound.

This definition must be followed by a regular sentence. Such behavior typically occurs at vertical asymptotes or discontinuities where the function is undefined or tends toward infinity.

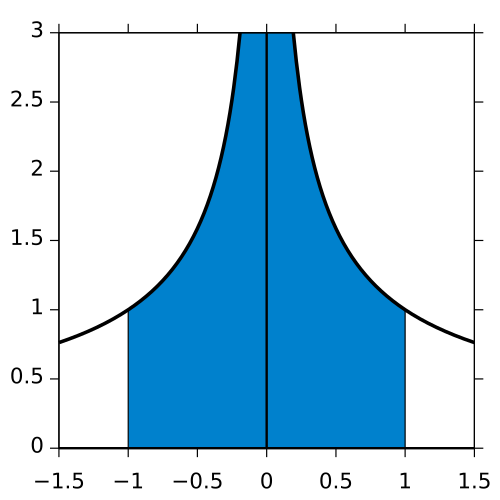
Graph of $y=\dfrac{1}{\sqrt[3]{x^{2}}}$ on $[-1,1]$ with the area between the curve and the $x$-axis shaded, illustrating an improper integral whose integrand is unbounded at the interior point $x=0$. The vertical spike highlights that even a finite interval can produce an improper integral when the function has a vertical asymptote. The page also includes the value $\int_{-1}^{1}\dfrac{dx}{\sqrt[3]{x^{2}}}=6$, which exceeds the recognition focus of this subtopic. Source.

Common signs that an integrand is unbounded include:

• Division by expressions that reach zero within the interval.

• Radical expressions where the denominator becomes zero.

• Functions with known asymptotes such as $1/(x-a)$ or $1/\sqrt{b-x}$.

Where Improper Behavior Appears

The unbounded point may occur:

• At the lower or upper limit of integration.

• At an interior point where the function is undefined.

• At multiple points, requiring careful recognition of each location of infinite behavior.

To recognize when the integrand is unbounded, students should visually inspect the algebraic structure of the function, identify potential division-by-zero situations, and consider whether the function tends toward $+\infty$ or $-\infty$ within the interval.

Comparing the Two Types of Improper Integrals

Distinguishing Between Infinite Limits and Unbounded Integrands

Improper integrals fall into two broad categories, and distinguishing between them guides later steps in evaluating or interpreting the integral.

• Type I (Infinite Limits): The issue arises from the domain extending without bound.

• Type II (Unbounded Integrands): The issue arises from the behavior of the function itself.

Both types share the important feature that the standard definition of a definite integral does not apply directly. Instead, improper integrals must be interpreted through limiting processes, but recognizing the need for these limits is the first conceptual step.

Why Recognition Matters

Conceptual and Analytical Importance

Identifying improper integrals helps students determine whether standard integration rules can apply and whether additional techniques are needed. Recognition ensures that:

• The integral is interpreted correctly as a limit.

• Students understand that not all definite integrals behave regularly.

• The nature of the integrand or interval dictates the appropriate analytic approach.

Situations Requiring Careful Inspection

Students should be prepared to classify an integral as improper whenever they observe:

• Limits extending to infinity.

• A denominator approaching zero.

• A radical or power expression yielding unbounded behavior.

• A graph showing vertical asymptotes within or at the boundaries of the interval.

Improper integrals occupy an essential place in calculus because they expand the applicability of integration to a wider range of problems. Recognizing them correctly ensures students approach them with the appropriate conceptual and analytic tools.