Indefinite integrals using substitution allow students to reverse the chain rule by rewriting complex expressions in a simpler variable, enabling easier computation of antiderivatives in common calculus settings.

Indefinite Integrals Using Substitution

When functions appear in composite or nested forms, direct application of basic antiderivative rules may be difficult. The substitution method transforms an integral into an equivalent form that is easier to evaluate by temporarily replacing part of the expression with a new variable. This technique is essential for reversing the chain rule and lies at the heart of many AP Calculus AB integrals requiring symbolic manipulation.

The Purpose of Substitution

The main goal of substitution is to simplify the integrand by identifying an inner function whose derivative also appears within the expression. The new substitution variable, traditionally $u$, allows the integrand to be rewritten in a more manageable form. Once the substitution is made, the integral resembles a basic antiderivative rule, which students can evaluate efficiently.

The Key Idea: Reversing the Chain Rule

Because differentiation applies the chain rule to composite functions, antidifferentiation often requires reversing it.

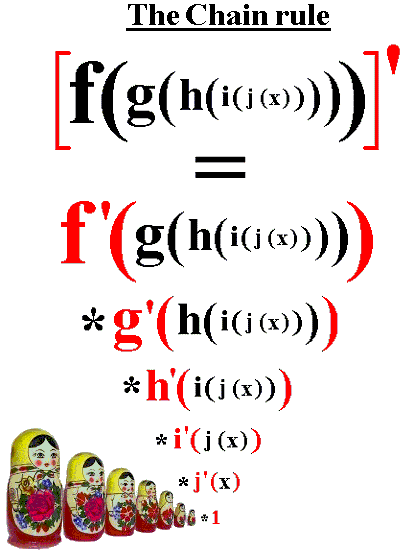
This diagram summarizes the chain rule, showing how the derivative of a composite function is formed from derivatives of inner and outer functions. It supports the idea that $u$-substitution reverses this structure to simplify integration. The symbolic layout includes slightly more detail than required but remains consistent with AP-level expectations. Source.

The substitution method relies on the fundamental relationship between differentials. When $u$ is defined as a function of $x$, the differential $du$ expresses how $u$ changes with respect to $x$. This relationship makes it possible to convert the integral into a form involving only $u$ and $du$ instead of $x$ and $dx$.

The Structure of a Substitution

A well-chosen substitution has several components that must work together. Students should learn to check that each step is coherent before proceeding. A typical substitution involves:

• Selecting a useful inner function as $u$.

• Computing $du$, which expresses the derivative of the substitution.

• Rewriting the integrand completely in terms of $u$ and $du$.

• Integrating using known formulas.

• Re-substituting the original variable after integrating.

After substitution, the integral typically becomes $\int f(u),du$, which can then be integrated using standard antiderivative rules.

This graph illustrates a function $f(x)$ with the signed area between the curve and the axis, reinforcing that integrals measure accumulated change. It connects substitution-based antiderivatives to the geometric meaning of integration. The colored positive and negative regions offer additional context consistent with the AP treatment of definite integrals. Source.

A full substitution must replace every appearance of the original variable from the integrand. Students should avoid leaving any $x$ terms behind once the rewriting process begins. The entire integrand must match the new variable system before the integration step is performed.

Identifying When Substitution Is Appropriate

Substitution is most effective when the integrand contains a composite expression whose derivative is also present, either exactly or up to a constant multiple. Students should look for:

• A function nested inside another function.

• A derivative of the inner function appearing elsewhere in the integrand.

• Expressions complicated enough that simpler antiderivative rules are insufficient.

• Structures reminiscent of the chain rule in reverse.

These indicators help determine whether substitution will appropriately simplify the integral or whether another strategy is needed.

Steps for Using Substitution in Indefinite Integrals

The process for applying substitution is systematic and consistent. AP Calculus AB students should learn to follow these steps carefully to avoid common algebraic errors. A well-organized approach helps ensure that the rewritten integral is valid and solvable.

• Choose an expression within the integrand to serve as $u$.

• Differentiate $u$ to compute $du$, expressing the differential in terms of $dx$.

• Rewrite the entire integrand using $u$ and $du$, ensuring no remnants of $x$ remain.

• Integrate the resulting expression with respect to $u$ using known antiderivative rules.

• Replace $u$ with the original expression to return the integral to the variable $x$.

• Add the constant of integration $C$, required for all indefinite integrals.

The Role of the Constant of Integration

Every indefinite integral must include the constant of integration $C$, since antiderivatives differ by vertical shifts. Substitution does not change this requirement. Regardless of how complex the transformation may be, the final answer always represents one member of a family of functions, each differing only by this constant.