AP Syllabus focus:
‘View substitution of variables as reversing the chain rule, allowing complicated composite functions to be rewritten in a simpler form for integration.’
Understanding u-substitution begins with linking integration to the chain rule in reverse, enabling composite expressions to be transformed into simpler integrals that preserve structure while easing computation.
Connecting u-Substitution to the Chain Rule
U-substitution is fundamentally a method for rewriting an integral so that a complicated composite expression becomes easier to integrate. This rewriting mirrors how the chain rule differentiates a composite function by multiplying the derivative of the outer function with the derivative of the inner function. When integrating, this relationship is reversed: instead of breaking a function apart, you compress the expression into a simpler form that aligns with a known antiderivative.
The Chain Rule and Its Reverse Relationship to Substitution
The chain rule states that the derivative of a composite function is .
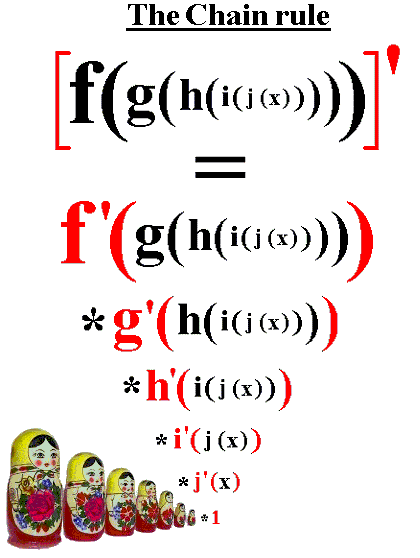
Diagram illustrating the chain rule for derivatives, showing how a composite function is built from an inner function and an outer function. The figure emphasizes that the derivative combines the rate of change of the outer function with the rate of change of the inner function, mirroring . This supports interpreting u-substitution as reversing this structure during integration. Source.
U-substitution relies on the fact that if differentiation distributes through a composition in this structured way, then integration can reverse the process by collapsing a related expression into a single, manageable function.
Chain Rule: The rule stating that the derivative of a composite function is the derivative of the outer function evaluated at the inner function multiplied by the derivative of the inner function.
When applying u-substitution, the goal is to recognize a portion of the integrand that acts like the inner function in the chain rule. By renaming this part with a new variable “u,” you create a pathway to reorganize the integrand into a more straightforward form. This process reflects viewing substitution as reversing the chain rule, which is emphasized directly in the syllabus description.
Why Substitution Works Conceptually
U-substitution works because integrals are affected by how variables change relative to one another. When you change variables from x to u, you also transform the differential to maintain the integrity of accumulated area. This transformation ensures the integral remains equal in value, even while expressed in a different variable.
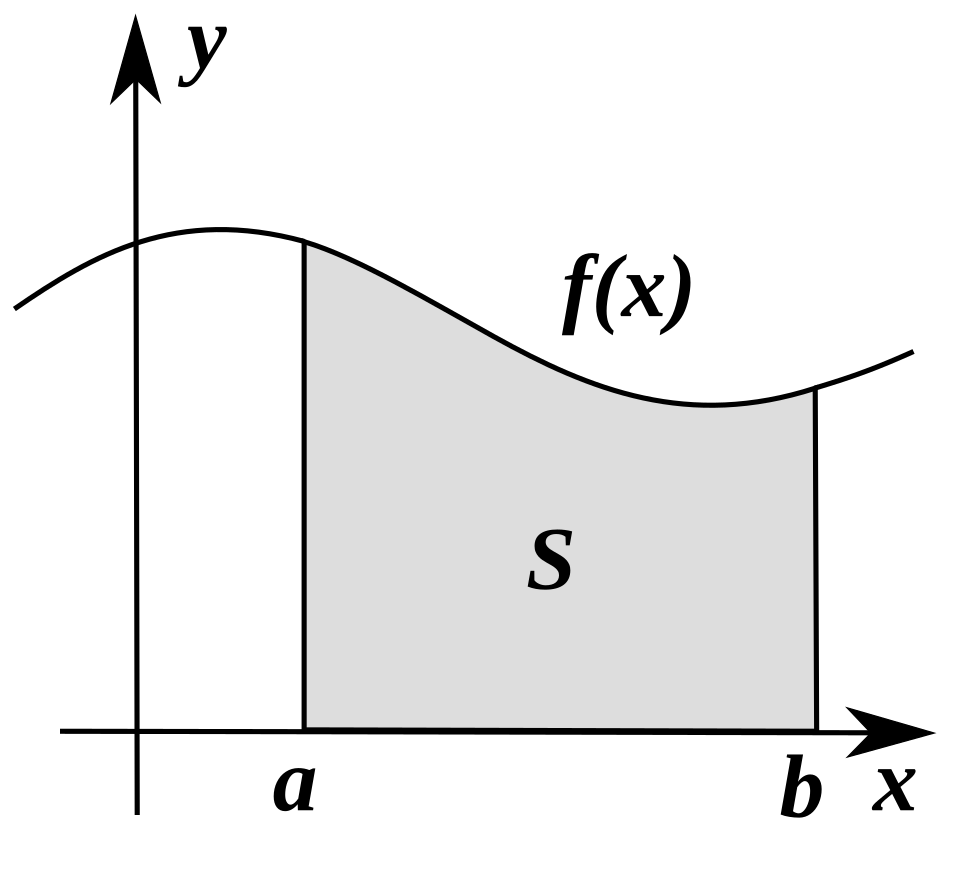
Graph of a function with the region between and shaded to represent the definite integral . The figure emphasizes that a definite integral corresponds to a fixed accumulated quantity, which must be preserved when variables are changed using u-substitution. The inclusion of the symbol and the explicit formula adds minor detail beyond the syllabus but remains fully consistent with AP Calculus AB expectations. Source.
The key is that the structure of the integrand mirrors the product produced by the chain rule, allowing you to reverse that structure thoughtfully and consistently.
u-Substitution: A technique for transforming an integral by defining a new variable to represent part of the integrand, thereby rewriting the integral in a simpler form.
After identifying the substitution, you reorganize the related differential. This part of the process is crucial because the differential expresses the rate at which the new variable changes relative to the original one, preserving the meaning of the integral's accumulated change.
Identifying a Useful Substitution
To apply u-substitution effectively, focus on expressions where one component’s derivative appears elsewhere in the integrand. Although AP Calculus AB does not require mastery of complex substitutions, students must recognize situations in which the integrand contains a composite function accompanied by something resembling its derivative.
Common indicators that suggest substitution may be effective include the following:
A composite function appears in the integrand.
The derivative is present as a factor or can be obtained with minor algebraic adjustment.
The integrand looks difficult to integrate in its current form but would match a known antiderivative after rewriting.
Once you choose a substitution, you replace both the inner expression and the differential in the integral. This creates a new integral entirely in terms of u, aligning with a familiar antiderivative formula.
The Role of Differentials in Substitution
Changing from x to u requires rewriting the differential. This preserves the integral’s meaning and ensures the new integral accurately represents the same accumulated area.
= New variable representing a chosen inner function (unitless unless context requires)
= Original variable of integration (unit depends on context)
= Differential expressing how changes with respect to (unit depends on context)
The differential equation reflects that substitution is not simply algebraic replacement; rather, it coordinates how changes in variables affect the integrand and its accumulated value.
Viewing Substitution as a Strategic Rewriting Process
Connecting u-substitution to the chain rule suggests a broader strategy for integration: look for structural patterns that hint at a reversed differentiation process. The chain rule compresses functions through differentiation; u-substitution decompresses them through integration. This perspective emphasizes:
Recognition of composite structure.
Rewriting the integrand using a new variable.
Preserving the accumulated change through the differential.
Integrating in the new variable and, when necessary, translating back to the original variable.
How This Subsubtopic Fits Within the Larger Integration Framework
This part of the syllabus highlights the conceptual foundation of substitution, rather than specific computational procedures. Students should understand why substitution works, how it mirrors differentiation in reverse, and how it enables the simplification of expressions in definite and indefinite integrals. By grounding substitution in the logic of the chain rule, AP Calculus AB emphasizes structural reasoning in integration rather than memorized techniques.
FAQ
Look for an expression nested inside another function, where the inner expression has a clear derivative present elsewhere in the integrand.
Common indicators include:
• A bracketed expression raised to a power
• A function multiplied by something resembling its own derivative
• A composition that becomes noticeably simpler if renamed as a single variable
If rewriting the integrand with a single substitution reduces the complexity of the expression, it is likely a suitable candidate.
You can still use the substitution as long as the missing constant or factor can be accounted for.
For example, if the derivative is present up to a constant multiplier, you may adjust the integral accordingly by compensating with a constant in the differential.
However, if the derivative is not present at all, the substitution will not simplify the integral and another method should be chosen.
The differential accounts for how the new variable changes relative to the original one, ensuring the integral corresponds to the same accumulated quantity.
Without replacing the differential, the substitution is only algebraic; the integral would no longer represent the correct change in area.
Changing the differential preserves the meaning of the integral by aligning the rate of change of the new variable with the transformed expression.
Yes, more than one substitution may technically work, but one is usually more efficient.
For example:
• A broad substitution might simplify only part of the integrand.
• A more targeted substitution, usually based on the inner function of a composition, will simplify the entire structure.
When several substitutions are possible, choose the one that results in the simplest rewritten integral and avoids unnecessary algebraic manipulation.
For indefinite integrals, you must convert back to the original variable after integrating, because the final expression must match the original variable of the function.
For definite integrals, you may either:
• Change the limits to match the new variable, avoiding back-substitution, or
• Integrate in terms of u and then convert back to x before applying the original limits.
Both approaches yield equivalent results when performed correctly.
Practice Questions
(1–3 marks)
The function h is defined by h(x) = f(g(x)), where f and g are differentiable functions. Explain how u-substitution in integration relates to the chain rule used to differentiate h.
(1–3 marks)
• 1 mark: Identifies that the chain rule differentiates a composite function by multiplying the derivative of the outer function by the derivative of the inner function.
• 1 mark: States that u-substitution reverses this process when integrating.
• 1 mark: Explains that choosing u as the inner function allows the integrand to be rewritten in a simpler form.
(4–6 marks)
Consider the integral ∫ 4x(x² + 5)³ dx.
(a) State a suitable substitution for evaluating this integral.
(b) Rewrite the integral in terms of your substitution.
(c) Hence write down the simplified integral in the new variable, without evaluating it.
(4–6 marks)
(a) (1 mark)
• States u = x² + 5 (or equivalent suitable substitution).
(b) (2 marks)
• 1 mark: Finds du = 2x dx or dx = du/(2x).
• 1 mark: Rewrites 4x dx correctly using the substitution (for example, 4x dx becomes 2 du).
(c) (1–2 marks)
• 1 mark: Writes the integral entirely in terms of u (e.g., ∫ 2u³ du or equivalent).
• 1 mark: Shows all parts of the integrand have been converted consistently into the u-variable.

