Euler’s Method constructs approximate solution values by stepping along a differential equation using tangent line slopes. It organizes each computational step into a structured, iterative table.

Constructing an Euler’s Method Table

Understanding how to construct an Euler’s Method table is essential for approximating solutions to first-order differential equations when no explicit solution is available. The process transforms the continuous behavior of a solution curve into a sequence of discrete steps. Each step uses the differential equation’s slope information to predict how the dependent variable changes as the independent variable increases.

Euler’s Method is built on the idea that a differentiable function behaves locally like its tangent line.

This figure illustrates one Euler step: starting at $(x_0, y_0)$, the slope $f(x_0, y_0)$ determines the tangent-line approximation used to estimate $y_1$. The blue curve shows the exact solution, while the red line represents the local linear approximation. The diagram emphasizes how Euler’s Method applies a constant slope across a short interval of length $h$. Source.

Core Components of an Euler’s Method Table

To construct a correct table, students must track several essential quantities. These quantities appear in each row and represent a single step of approximation.

• The current value of the independent variable

• The current approximate value of the dependent variable

• The derivative value, computed from the differential equation using the current values

• The updated value of the dependent variable, produced by using the step size and slope to estimate the change

The central recurrence idea connects these quantities and drives the entire method forward.

The update equation supports the creation of the next row in the table, producing a sequence of approximated points that follow the expected behavior of the solution curve.

Step Size and Table Structure

A critical organizational choice in creating the table is selecting the step size $\Delta x$. A smaller $\Delta x$ gives more rows and typically improves accuracy, because each tangent-line approximation is applied over a shorter interval. A larger step size yields fewer rows but may introduce greater accumulated error. Regardless of the step size, a well-constructed table must systematically include every dependent quantity required to execute each iterative update.

The standard format of an Euler’s Method table includes columns such as:

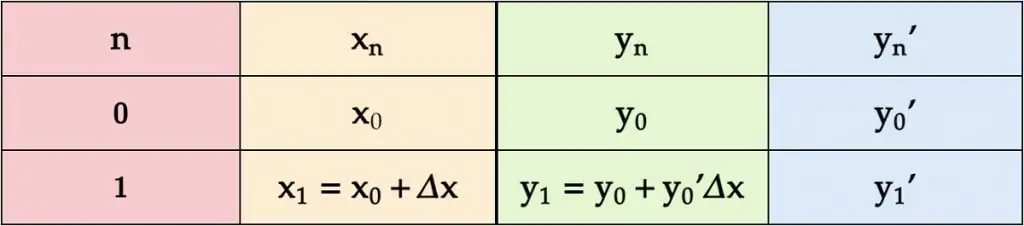
This table displays the standard structure of Euler’s Method, listing $n$, $x_n$, $y_n$, and the derivative $y_n'$. It highlights how each step records the independent variable, the approximate value, and the slope from the differential equation. The numerical entries reflect one example, but the column organization matches the AP Calculus AB requirements. Source.

• $x_n$: the independent variable at step $n$

• $y_n$: the approximate solution value at step $n$

• $f(x_n, y_n)$: the derivative value computed from the differential equation

• $y_{n+1}$: the updated approximate value obtained using the Euler update

Importance of Derivative Evaluation

A key idea in constructing an Euler’s Method table is the proper evaluation of the derivative function. The differential equation expresses the rate of change of the dependent variable in terms of the independent variable and, sometimes, the dependent variable itself. For each step, students must substitute the current $x_n$ and $y_n$ into the derivative expression. Because the functional relationship can be nonlinear, every row may produce a different slope. This means the method dynamically adapts to the behavior of the differential equation, even though each interval uses a simple linear estimate.

Iterative Structure and Flow of the Table

A completed Euler’s Method table reflects a sequence of approximations, each one dependent on those that came before it.

The iterative pattern continues until students reach the desired final value of the independent variable. Although each step individually approximates the tangent line, together they trace an approximate path that aligns with the expected direction and curvature suggested by the differential equation.

The general process follows this structured progression:

• Select the initial point $(x_0, y_0)$ provided by the problem.

• Choose a step size $\Delta x$ appropriate for the desired interval and accuracy.

• Compute the derivative value $f(x_n, y_n)$ for the current step.

• Use the Euler update to compute $y_{n+1}$.

• Increase the independent variable by the step size to determine $x_{n+1}$.

• Record all values in the table before moving to the next step.

This discrete organization helps track how approximate values evolve and ensures that the method is transparent and reproducible.

The Role of the Table in Understanding Solution Behavior

Constructing the Euler’s Method table provides insight into how a differential equation governs the evolution of its solutions. While the method does not guarantee precise accuracy, especially for large steps or rapidly changing functions, it offers a valuable way to analyze solution tendencies locally and globally. By observing how derivative values rise, fall, or remain stable across the rows, students gain qualitative understanding of the underlying differential relationship.

Because each step relies on the slope supplied by the differential equation, the table serves as a record of how the differential equation guides the solution curve’s direction. Even without graphing, the structured list of approximate values reveals whether the solution increases, decreases, or changes its rate of growth as the independent variable progresses.

Practical Significance of the Table Format

The required table format reinforces the AP Calculus AB emphasis on linking symbolic rate-of-change information to numerical approximations. By explicitly listing values of the derivative alongside values of $x$ and $y$, the table highlights how the differential equation drives every update. This organization promotes conceptual understanding and prepares students to analyze numerical approximations in more advanced modeling contexts.