Euler’s method approximates solutions to differential equations by stepping along tangent lines, and understanding how step size influences accuracy is essential for evaluating the reliability of numerical estimates.

Step Size and Its Role in Euler’s Method

Euler’s method provides a numerical approximation to a solution of a first-order differential equation by repeatedly using the slope given by the differential equation itself. The step size, often denoted by $h$, determines how far the approximation moves along the independent variable before recalculating the slope. Because this technique follows a local linearization, the choice of step size directly affects how closely the approximations follow the true solution curve.

This figure illustrates Euler’s method as a sequence of tangent-line steps approximating an unknown solution curve. The smooth blue curve represents the exact solution, while the red polygonal path shows how successive linear segments approximate it. Students should focus on how each short step stays close to the curve, highlighting why step size matters for accuracy. Source.

A small step size produces more recalculations of the slope, allowing the numerical path to adjust more often to the curvature of the true solution. A larger step size forces the approximation to extend each tangent line farther before correcting direction, resulting in greater deviation.

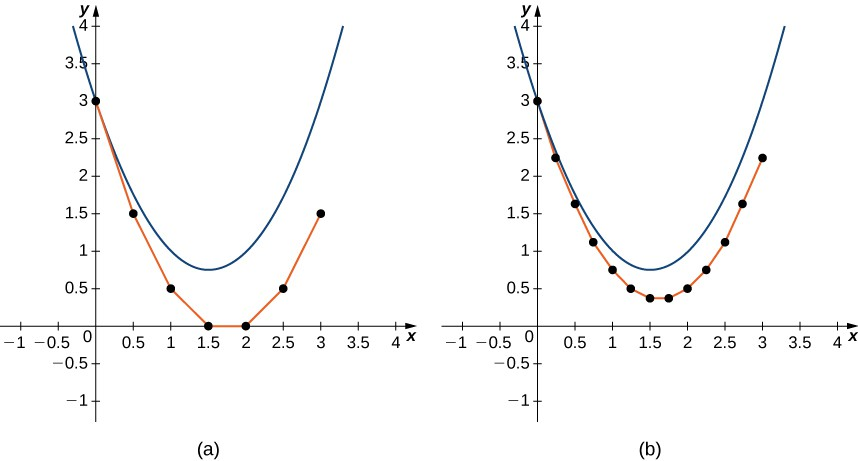
This pair of graphs compares Euler’s method for the same initial value problem with different step sizes. The plot with the smaller step size more closely follows the underlying curve, while the larger step size produces a rougher approximation. Students should note how increasing the number of smaller steps improves agreement with the solution. Source.

Understanding Local Versus Global Accuracy

Euler’s method introduces local error at each individual step and global error across the full interval of approximation. Both forms of error are influenced by step size, though global error accumulates step-by-step.

Local Truncation Error

Local truncation error refers to the error introduced within one Euler step from using a tangent line to approximate a curved solution. Smaller step sizes reduce this error because they shorten each tangent-based prediction, giving curvature less opportunity to cause deviation.

Global Accumulated Error

Since Euler’s method builds upon each previous approximation, early inaccuracies can propagate. Reducing step size decreases the magnitude of each error and increases the number of corrections, which usually reduces total accumulated error across the interval.

The Update Formula and Its Dependence on Step Size

The central mechanism of Euler’s method is the update rule, which determines how each new approximate value is computed from the previous one. This rule shows explicitly how step size contributes to each approximation.

Because the slope is multiplied by the step size, the magnitude of each update depends directly on $h$. When $h$ is large, each tangent-line estimate pushes the approximation farther, increasing the likelihood of overshooting or undershooting the true path.

After applying the update repeatedly, students begin to see visually and numerically how cumulative changes scale with $h$.

Why Smaller Step Sizes Improve Accuracy

Better Representation of Curvature

The true solution to a differential equation may curve sharply or subtly depending on the behavior of its derivative. Since Euler’s method uses straight lines to approximate this curve, smaller step sizes allow the lines to “hug” the true curve more closely.

More Frequent Slope Recalculations

Because differential equations often have slopes that change with both $x$ and $y$, smaller steps recalculate these changing slopes more often. Frequent updates better reflect the dynamic nature of the solution.

Reduced Error Propagation

Large errors early in the approximation can distort the entire sequence of approximations. Smaller steps limit the size of each individual error, limiting the distortion in later approximations.

Practical Interpretations of Step Size Choices

When Larger Steps Are Tempting

In practice, larger step sizes may be chosen when:

• A rough approximation is sufficient

• Time or computational resources are limited

• The interval of interest is very long and a quick overview is desired

However, these choices come with clear drawbacks. Large steps often fail to capture oscillations, concavity changes, or rapid variations in the slope.

When Smaller Steps Are Preferable

Students should recognize that smaller step sizes are especially important when:

• The derivative changes rapidly

• The solution curve bends noticeably

• Long-term behavior is sensitive to initial conditions

• High accuracy is required for interpretation or modeling

Small steps provide stability and reliability across these contexts.

Balancing Efficiency and Precision

Even though smaller steps produce more accurate approximations, they also require more computations. When the step size is excessively small, the method becomes inefficient without substantial gains in meaningful precision. In many contexts, an optimal step size balances acceptable accuracy with manageable computational work.

How Step Size Influences Graphical Behavior

In a graphical representation of Euler approximations, each step corresponds to a short line segment aligned with the slope at that point. As step size decreases:

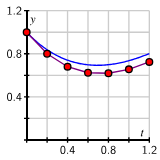
This graph displays a smooth exact solution curve alongside the polygonal path generated by Euler’s method for a chosen step size. The straight segments approximate the true function but do not match its curvature perfectly, illustrating persistent error even with smaller steps. Some additional contextual details, such as figure numbering, extend beyond the AP syllabus but do not affect the conceptual takeaway. Source.

• The approximation curves more smoothly

• Sharp deviations from the true solution diminish

• The piecewise linear path increasingly resembles the actual solution

Conversely, large step sizes appear jagged, exaggerated, and less aligned with the underlying slope field.

Key Takeaways About Step Size and Accuracy

• Step size directly affects error, both locally and globally.

• Smaller steps generally improve accuracy, allowing the approximation to respond more closely to curvature.

• Larger steps decrease reliability, especially when slopes vary significantly.

• Students must interpret the impact of step size when deciding whether an Euler approximation is consistent with the behavior of the underlying differential equation.