AP Syllabus focus:
‘The washer method uses V = ∫ π[(outer radius)² − (inner radius)²] dx or dy to find volumes of solids of revolution with ring-shaped cross sections.’
The washer method determines volumes of solids created by rotating regions around principal axes, using circular cross sections defined by outer and inner radii.
Washer Method for Principal Axes
This subsubtopic focuses on building the washer method volume formula for solids of revolution generated about the x-axis or y-axis, where slicing the solid perpendicular to the axis of rotation produces a ring-shaped two-dimensional cross section. These washers generalize the disc method by allowing an inner hollow region, enabling the measurement of solids formed from regions bounded by two curves instead of one. The core idea is viewing volume as accumulated areas of washers whose radii depend on the location of the bounding curves.
Understanding Ring-Shaped Cross Sections
When a region that lies between two curves is revolved around a principal axis, each resulting slice perpendicular to the axis forms a washer, which is a circular annulus. The washer has two defining measurements:
an outer radius, the distance from the axis of rotation to the farther curve
an inner radius, the distance from the axis to the nearer curve
If the inner radius equals zero, the washer becomes a disc, showing how the washer method naturally extends earlier ideas.
Outer Radius: The distance from the axis of revolution to the farther bounding curve, determining the outer edge of each washer’s area.
A washer’s area reflects the difference between the areas of two circles, creating the characteristic ring-shaped cross section that accumulates along the interval of revolution.
Inner Radius: The distance from the axis of revolution to the nearer bounding curve, creating the hollow portion inside each washer.
This geometric relationship provides the structural basis for the washer formula used to determine total volume by integration.
When a region between two graphs is revolved about the x- or y-axis and leaves a ‘hole’ along the axis, each cross section is a washer.
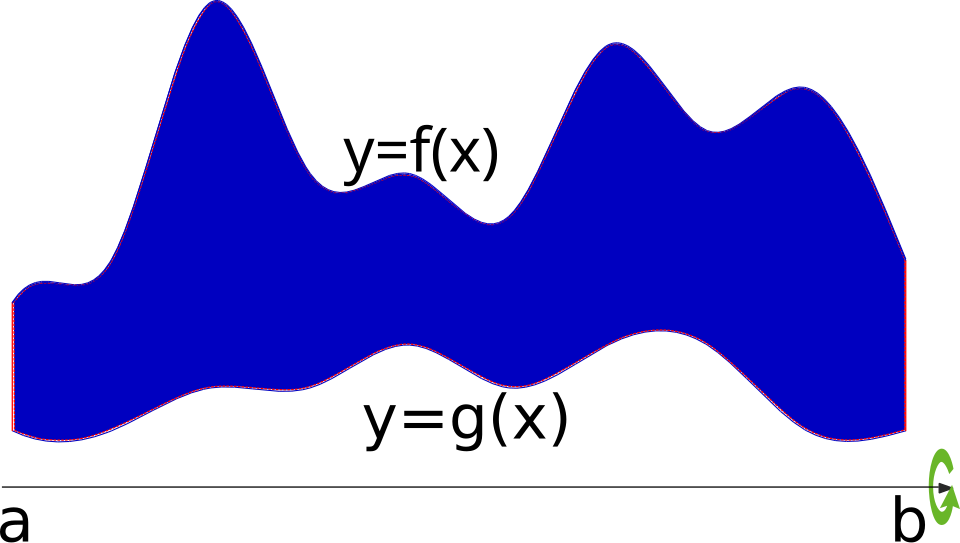
A region between two curves is revolved around a horizontal axis to generate a solid of revolution. The outer and inner graphs determine the outer radius and inner radius of each washer. This picture shows how the formula represents accumulation of washer areas. Source.
The Washer Method Formula for Principal Axes
To compute volume using washers, AP students use a definite integral that expresses the accumulated area of washers across the chosen interval. When revolving around a principal axis, the cross-sectional area is defined in terms of squared radii.
= Distance from axis to farther curve
= Distance from axis to nearer curve
This formula appears in an equivalent form with when the solid is sliced perpendicular to the y-axis, emphasizing the versatility of the method in different geometric contexts.
A key goal of this topic is ensuring that students correctly interpret curves as describing radii measured perpendicularly to the axis of rotation. Maintaining the correct variable of integration ensures that each washer is properly oriented and that its area corresponds to the physical geometry of the generated solid.
Relating Radii to Bounding Functions
Identifying outer and inner radii is central to applying the washer method accurately. Because radii always represent distances to the axis, a student must express these radii using either function values or differences between function values and the axis location. Proper interpretation depends on the axis of revolution:
Revolving Around the x-Axis
Perpendicular slices are vertical, so radii are written using functions of x.
Outer radius: the greater vertical distance from the x-axis
Inner radius: the lesser vertical distance from the x-axis
Revolving Around the y-Axis
Perpendicular slices are horizontal, so radii are written using functions of y.
Outer radius: the greater horizontal distance from the y-axis
Inner radius: the lesser horizontal distance from the y-axis
These distinctions highlight why alignment between the variable of integration and the direction of slices is essential for correct application.
Each washer’s area is the area of the outer circle minus the area of the inner circle, so the integrand must use the difference rather than either radius alone.
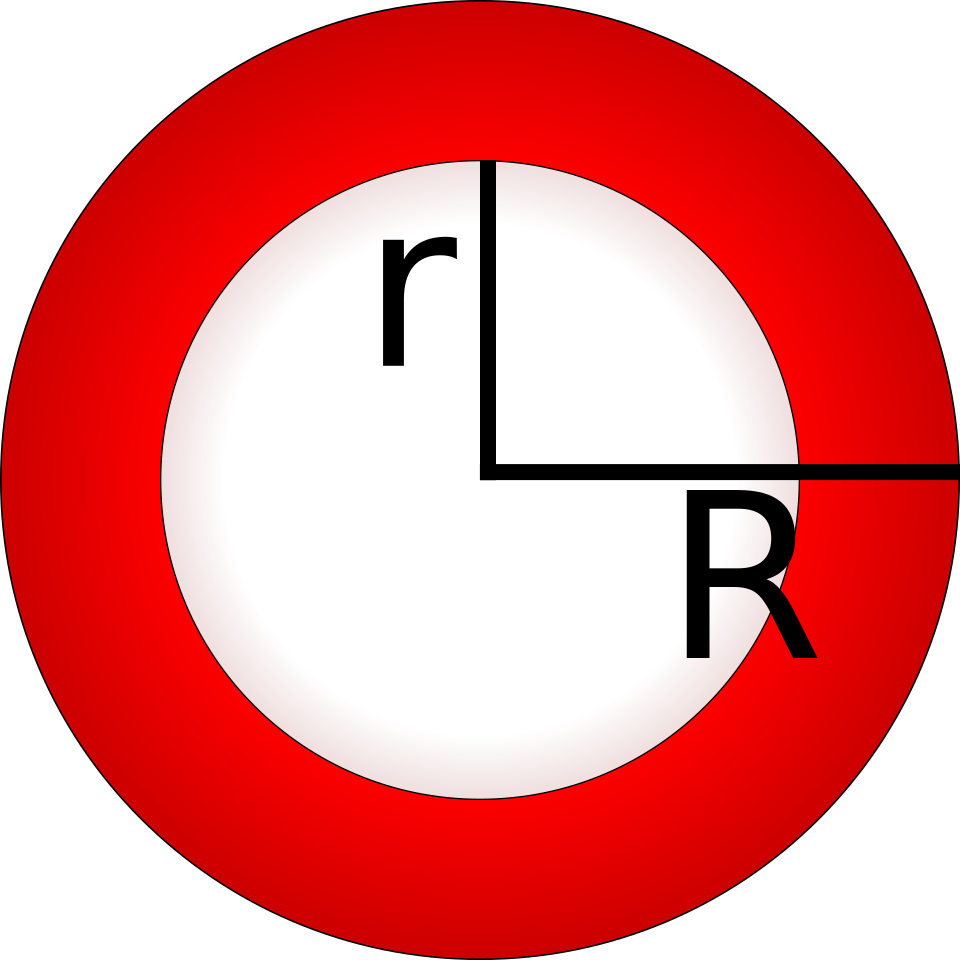
This annulus represents the cross section of a washer, with outer radius and inner radius . Its area is , matching the expression used in the washer method. The image includes some additional geometric markings, but its essential feature is the ring shape formed by two radii. Source.
Structured Process for Using the Washer Method
Bullet points help emphasize the procedural clarity required by the syllabus:
Identify the axis of revolution and determine whether washers are oriented perpendicular to the x-axis or y-axis.
Express the outer radius as the distance from the axis to the farther curve.
Express the inner radius as the distance from the axis to the nearer curve.
Determine the appropriate interval for integration using the variable aligned with the slicing direction.
Substitute radii into the washer formula to construct the definite integral.
Evaluate or interpret the integral to represent the total accumulated volume.
Conceptual Interpretation
The washer method interprets volume as accumulation of cross-sectional areas formed by revolving a two-curve region around a principal axis. Each washer represents one infinitesimally thin slice of volume, where subtracting the inner circular area from the outer circular area ensures that the hollow part of the solid is correctly represented. This approach demonstrates how understanding geometric distance and curve behavior directly informs the integral that models the solid’s volume.
FAQ
A region produces washers when the rotation creates a hollow centre, meaning the nearest part of the region to the axis does not lie directly on the axis.
Check whether two separate curves define distances from the axis. If both curves have positive distance from the axis on the interval, a washer is formed.
If the inner distance is consistently zero, the solid will instead use the disc method.
Students often choose radii based on which curve is larger in value, without checking the orientation of the slices.
For the washer method:
• If integrating with respect to x, compare vertical distances from the axis.
• If integrating with respect to y, compare horizontal distances.
Always measure radii perpendicularly from the axis of rotation, not along the curve itself.
Cross-sectional area is always a circular or annular region, so it is determined by the formula for the area of a circle.
Because the radius describes a linear distance, its square naturally appears when converting the distance function into an area function.
The integral accumulates these circular or annular areas, which is why squared radii remain essential throughout.
Both approaches are equivalent only if the region is fully describable as functions of x or as functions of y across a single continuous interval.
If the region cannot be expressed cleanly in one orientation (for example, if the boundary is not single-valued), the integrals may differ in complexity.
Choosing the simpler orientation can eliminate unnecessary splitting of the integral or re-expression of the curves.
At isolated points where the inner radius becomes zero, the washers briefly behave like discs.
This does not break the method. The integral naturally accounts for these points because a radius of zero simply contributes a circular cross-section at that location.
However, ensure the region does not cross the axis, as this would require re-evaluating which curve defines the radii on different subintervals.
Practice Questions
A region in the plane is bounded above by the curve y = 4, below by the curve y = x, and lies between x = 0 and x = 2. The region is revolved about the x-axis.
Using the washer method, write down a definite integral that represents the volume of the resulting solid.
(3 marks total)
• Correct identification of outer radius: R(x) = 4. (1 mark)
• Correct identification of inner radius: r(x) = x. (1 mark)
• Correct integral for volume: integral from 0 to 2 of pi(4^2 − x^2) dx. Limits and integrand must be correct. (1 mark)
The region enclosed by y = 6 − x, y = 2, and the y-axis is revolved about the y-axis to form a solid.
(a) Sketch or clearly describe the region and identify the outer and inner radii in terms of y.
(b) Set up, but do not evaluate, the integral representing the volume of the solid using the washer method.
(c) Explain why the washer method is appropriate rather than the disc method for this solid.
(6 marks total)
(a) (2 marks)
• Correct description of the region: bounded by the line y = 6 − x, the horizontal line y = 2, and x = 0 (the y-axis). (1 mark)
• Correct outer and inner radii in terms of y: outer radius R(y) = 6 − y, inner radius r(y) = 0. (1 mark)
(b) (3 marks)
• Correct limits of integration: from y = 2 to y = 6. (1 mark)
• Correct washer expression with radii in terms of y. (1 mark)
• Correct integral: integral from 2 to 6 of pi[(6 − y)^2 − 0^2] dy. (1 mark)
(c) (1 mark)
• Correct explanation: The region has a hollow centre when revolved about the y-axis, so the cross-sections are washers rather than discs. (1 mark)

