Ring-Shaped Cross Sections and the Washer Idea

A solid of revolution formed from a region with a hollow center produces washer-shaped cross sections, allowing volume to be computed by integrating circular areas with missing inner portions.

Understanding Ring-Shaped Cross Sections

When a plane region that does not touch the axis of revolution is revolved around that axis, the resulting three-dimensional slices perpendicular to the axis are not solid discs but washers. A washer resembles a flat ring: a circular region with another circular region removed from its center. This structure emerges naturally whenever the original region includes a gap between part of the boundary and the axis of revolution. The gap forms the inner radius, while the outer boundary of the region forms the outer radius. The distinction between these radii is essential because it determines how much material appears in each cross section of the solid.

Because washers have a central hole, their cross-sectional area must account for two circular measurements: the outer circle's area and the inner circle's area. Each slice’s area is the difference between these two, making the washer method a natural extension of the disc method. The method relies on understanding how radii vary along the chosen axis and how those radii arise from the geometry of the region being revolved.

Each thin slice perpendicular to the axis is therefore a washer: a circular ring with an outer edge and a central hole rather than a solid disk.

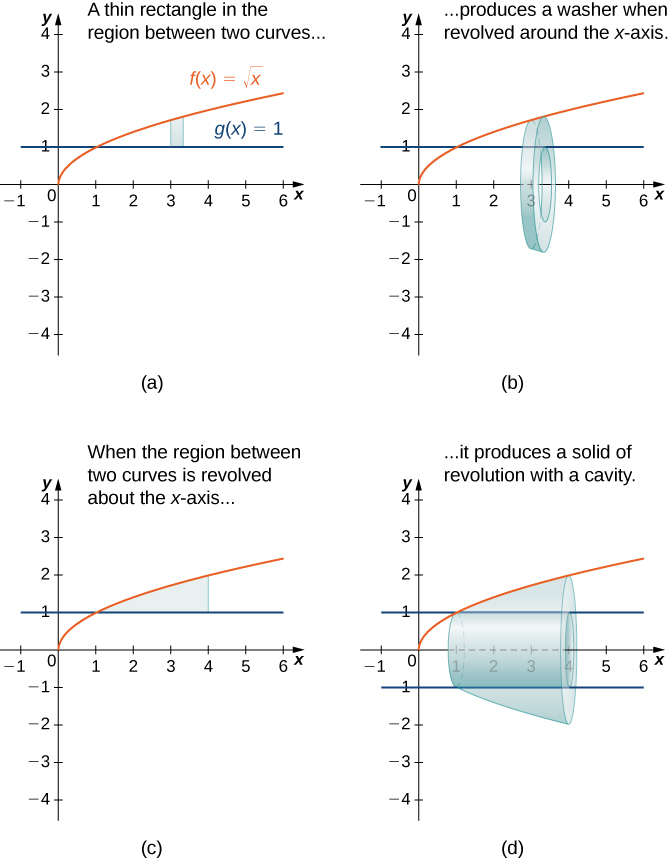
This diagram shows how a planar region between two curves generates a washer-shaped cross section and a solid of revolution when rotated about the axis. It emphasizes that each slice is a ring because the region does not extend to the axis of rotation. Extra details such as the specific curves and interval offer helpful context beyond the syllabus requirements. Source.

The Concept of Radii in Washer Problems

The outer radius is defined as the distance from the axis of revolution to the outer boundary of the region.
The inner radius is the distance from the axis to the inner boundary, which creates the hole. These distances are essential because they determine the shape and size of each washer. The difference between the squared values of these radii generates the cross-sectional area used to accumulate volume.

A sentence must come between definition blocks to maintain clarity and avoid clustering of formal statements.

These radii depend on the orientation of the revolution. If the solid is revolved around the x-axis, the radii must be expressed as vertical distances, written as functions of the variable of integration. If the solid is revolved around the y-axis, the radii correspond to horizontal distances and must be written in terms of the variable appropriate for integrating with respect to y. Understanding these directional relationships ensures that the formulation of the volume integral correctly reflects the geometry of the solid.

Revolving such a region around an axis that runs outside the region produces a three-dimensional solid with a hollow core extending along the axis of revolution.

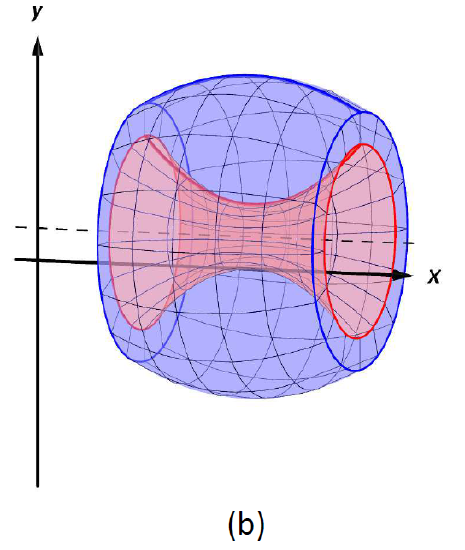
These diagrams illustrate how revolving a region that does not touch the axis produces a hollow solid. The images highlight the central void and the outer surface that together define washer-shaped slices. Labels such as R(x) and r(x) provide additional detail not strictly required by the syllabus but support understanding of inner and outer radii. Source.

Connecting Washers to Accumulated Volume

The washer method reflects the broader Calculus AB emphasis on viewing volume as an accumulation of infinitesimal quantities. In this case, the infinitesimal quantity is the area of a washer-shaped slice, and the volume is the accumulated sum of such slices across the interval of revolution. The method formalizes this idea using a definite integral whose integrand captures the difference between the outer circular area and the inner circular area.

A sentence here provides continuity before further mathematical structure is introduced, ensuring the exposition remains readable and well paced.

This integral expresses the essential idea: volume is the accumulation of cross-sectional areas, each computed as a ring formed by subtracting the area of the inner circle from the area of the outer circle. The method is particularly effective when the region’s boundaries are clearly identified and when both radii can be expressed as functions of a single variable across the interval. In AP Calculus AB, this technique is used only for solids revolved around the x- or y-axis when a central cavity exists.

Identifying When to Use the Washer Method

Students should recognize the need for washers whenever the region being revolved does not touch the axis of revolution or when the region is bounded by two separate functions relative to the axis. Key indicators include:

• The presence of a gap between part of the region and the axis.

• A boundary curve that produces an inner radius smaller than the outer radius.

• A region enclosed by two curves, where rotation causes the nearer curve to form the inner boundary of the washer.

• A geometric description that specifies a hole in the resulting solid.

We usually describe the distance from the axis to the outer curve as the outer radius and the distance from the axis to the inner curve as the inner radius, each measured along the same perpendicular slice.

Visual and Conceptual Interpretation

Visualizing washers helps reinforce the conceptual understanding of volume as accumulated area. Each slice resembles a ring whose thickness corresponds to the differential element along the axis of revolution. As these slices stack, they build the overall three-dimensional shape. This perspective aligns with the AP Calculus AB emphasis on interpreting integrals as accumulated change, connecting geometric intuition with analytic computation.

Understanding washer-shaped cross sections ensures students can construct accurate integrals for volumes of revolution whenever a hollow interior appears in the solid.