Applying the Washer Method Around Coordinate Axes (8.11.3) | AP Calculus AB Notes

AP Syllabus focus:
‘Students set up washer integrals for revolution about the x- or y-axis, carefully identifying outer and inner radii from the graphs or equations of the bounding curves.’

This subsubtopic develops the skill of constructing definite integrals using the washer method for solids of revolution, focusing on identifying radii and correctly selecting the variable of integration when revolving regions around coordinate axes.

Applying the Washer Method Around Coordinate Axes

The washer method extends the idea of slicing a solid into thin circular rings. When a region that does not touch the axis of revolution is rotated around the x-axis or y-axis, the resulting solid has ring-shaped cross sections, each defined by an outer radius and an inner radius. Understanding how to identify these radii is essential for correctly formulating the corresponding definite integral.

Understanding Washer Cross Sections Around Coordinate Axes

A washer arises when revolving a region that lies away from the axis of revolution, creating a hollow center in each circular slice.

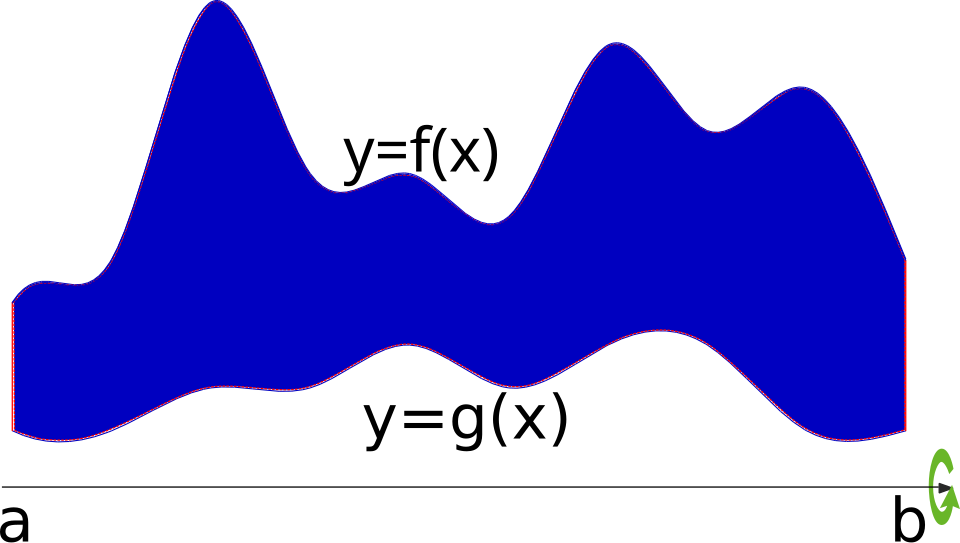
A planar region is shown next to its axis of revolution and the three-dimensional solid produced by rotating the region. The picture emphasizes how revolving a 2D area around an axis produces a solid whose cross sections are circular. The specific curves and numerical scales included go beyond AP Calculus AB requirements and serve only as illustration. Source.

Washer: A cross-sectional shape formed by a circular ring with an empty center when a region not touching the axis of revolution is rotated around an axis.

Such washers appear naturally anytime the boundary curves of the region are separated from the axis of revolution. The radius functions describe the distance from those curves to the axis.

Determining Outer and Inner Radii

Correctly identifying the radii is the central task in applying the washer method. The outer radius corresponds to the boundary curve furthest from the axis of revolution, while the inner radius corresponds to the boundary curve closer to the axis.

When revolving around the x-axis:

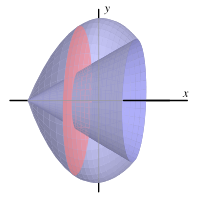
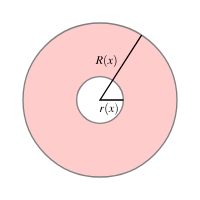
The left panel shows a region between two curves revolved about the x-axis to form a solid of revolution. The right panel isolates a washer slice, clearly showing how the inner radius $r(x)$ and outer radius $R(x)$ are measured vertically from the axis. The particular curves and intersection values displayed exceed the AP syllabus requirements and are purely illustrative. Source.

The radii are measured vertically.
Expressions must be written in terms of $x$ if slices are perpendicular to the axis.

When revolving around the y-axis:

The radii are measured horizontally.
Expressions must be written in terms of $y$ if slices are perpendicular to the axis.

These conventions ensure that each radius reflects the geometric distance appropriate to the direction of rotation.

The Washer Method Integral for Coordinate Axes

The standard formula for volume using washers around a coordinate axis is expressed as an integral of the difference between squared radii.

$V = \int_a^b \pi[(R(x))^2 - (r(x))^2],dx$
$R(x)$ = Outer radius measured from the axis of revolution
$r(x)$ = Inner radius measured from the axis of revolution
$[a,b]$ = Interval of integration along the axis

This form applies when revolving around the x-axis with radii expressed as functions of $x$ . For revolution around the y-axis, the corresponding expression uses $y$ as the variable, and radii depend on the horizontal distance to the curves.

A clear sentence is placed here to ensure separation between equation blocks.

$V = \int_c^d \pi[(R(y))^2 - (r(y))^2],dy$
$R(y)$ = Outer radius measured horizontally from the axis
$r(y)$ = Inner radius measured horizontally from the axis
$[c,d]$ = Interval of integration along the axis

Steps for Setting Up Washer Method Integrals

Students should follow a logical process when constructing washer integrals involving rotation around the x-axis or y-axis:

Identify the axis of revolution, confirming whether it is the x-axis or y-axis.
Determine the orientation of slices:
- Perpendicular to the x-axis → integrate with respect to $x$ .
- Perpendicular to the y-axis → integrate with respect to $y$ .
Locate the outer radius as the larger distance from the axis to the appropriate curve.
Locate the inner radius as the smaller distance from the axis to the bounding curve or axis.
Square each radius, as the area of a washer depends on squared radii.
Form the integrand $\pi[(\text{outer})^2 - (\text{inner})^2]$ .
Determine the correct limits of integration, matching the axis variable.
Write the definite integral, ensuring that all expressions match the chosen variable.

Common Washer Scenarios Around Coordinate Axes

Students frequently encounter situations such as:

A region bounded by a curve and the x-axis, rotated around the x-axis.
- The inner radius is zero because the region touches the axis.
- Washers become discs, but the structure follows the same formula.
A region bounded between two functions above the x-axis, rotated around the x-axis.
- The outer radius comes from the top function’s height.
- The inner radius comes from the lower function’s height.
A region to the right of the y-axis rotated around the y-axis.
- Radii become horizontal distances, requiring expressions in terms of $y$ for integration.

Each case requires identifying which curve is farther from the axis, ensuring proper alignment with the washer framework.

Reading Graphs and Equations to Determine Radii

Determining radii often requires careful interpretation of graphs. Students need to:

Observe relative vertical or horizontal distances to the axis.
Identify curve ordering across the interval.
Translate distances into algebraic expressions accurately.
Confirm that the selected functions correspond to outer and inner radii on the chosen interval.

This geometric reasoning ensures that the integrals correctly represent the volume formed by revolving the region around the coordinate axis.

FAQ

Choose the variable based on the direction of the slices. If washers are perpendicular to the x-axis, the radii must be written as functions of x. If washers are perpendicular to the y-axis, express all radii as functions of y.

This prevents mixing variables and ensures the integral corresponds to how the washers are formed along the axis of rotation.

Students often confuse vertical and horizontal distances. Radii must always be genuine distances measured straight to the axis of revolution.

Misidentifying which curve is further from the axis can also reverse the outer and inner radii, producing a negative integrand.

Ask whether the region touches the axis of rotation. If any boundary curve lies directly on the axis, the inner radius is zero, and the method reduces to discs.

If every point in the region is separated from the axis, washers must be used because the interior of each slice is hollow.

The area of each cross section is the area of a ring, which equals the area of a large circle minus the area of a smaller circle.

Since circle area depends on radius squared, each radius must be squared separately before subtraction.

The limits represent how far the washers extend along the axis of rotation. They mark the interval over which the slices accumulate to form the entire solid.

• For rotation about the x-axis, limits are x-values.
• For rotation about the y-axis, limits are y-values.

Always align the limits with the variable used in your radius expressions.

Practice Questions

(1–3 marks)
A region in the first quadrant is bounded above by the curve y = 4, below by the curve y = x, and on the left by the y-axis. The region is revolved about the x-axis.
Write down the integral that represents the volume of the resulting solid using the washer method.

Question 1 (1–3 marks)
• 1 mark: Identifies outer radius as 4 (distance from y = 4 to x-axis).
• 1 mark: Identifies inner radius as x (distance from y = x to x-axis).
• 1 mark: Writes the correct integral for the volume: integral from 0 to 4 of pi(4 squared minus x squared) dx.

(4–6 marks)
Consider the region enclosed between y = 6, y = 2x, and the y-axis. The region is revolved about the y-axis.
a) State expressions for the outer radius and inner radius of a typical washer.
b) Write down the definite integral representing the volume of the solid formed.
c) Explain why washers (and not discs) are required for this problem.

Question 2 (4–6 marks)
a)
• 1 mark: Outer radius stated as the horizontal distance from y-axis to the curve y = 6, expressed as x = 0 to x = 3 (or equivalently radius = 3).
• 1 mark: Inner radius stated as the horizontal distance from y-axis to y = 2x, expressed as x = y/2.

b)
• 1 mark: Writes volume integral in terms of y: integral from y = 0 to y = 6 of pi[(3 squared) − (y/2 squared)] dy.
• 1 mark: Correct structure of a washer integral (outer squared minus inner squared).

c)
• 1 mark: States that washers are required because the region does not touch the axis of rotation; an inner gap exists, so discs would not describe the hollow interior.

Try All Topic Practice Questions

Written by:

Dr Rahil Sachak-Patwa

Oxford University - PhD Mathematics

Rahil spent ten years working as private tutor, teaching students for GCSEs, A-Levels, and university admissions. During his PhD he published papers on modelling infectious disease epidemics and was a tutor to undergraduate and masters students for mathematics courses.