AP Syllabus focus:
‘Graphs and diagrams help students visualize which function gives the outer radius, which gives the inner radius, and how the region generates the solid when revolved.’
The average student gains confidence with washer-method applications by closely interpreting visual information, since diagrams reveal radius relationships essential for writing correct volume integrals.
Understanding Visual Interpretation in Washer Problems
Graphs and diagrams play a central role in washer-method volume problems because they illustrate how a region is revolved around an axis and how radii must be identified to construct the correct integral. In these problems, a washer represents a circular slice with a hole, formed when a region bounded by curves is revolved around a line. Understanding which curve determines the outer radius and which determines the inner radius is essential for applying the washer method correctly. Students rely on images to distinguish vertical or horizontal distances, identify boundaries, and see how the generated solid takes shape.
When a washer forms, two radii appear: the distance from the axis of revolution to the farther boundary curve, and the distance from the axis of revolution to the closer boundary curve. These distances are extracted directly from the diagram by reading vertical or horizontal separations. The clarity provided by diagrams ensures that the volume integral reflects the actual geometry of the revolved region rather than an algebraic interpretation alone.
Graphs and diagrams show how these slices stack and how their radii vary across the interval.
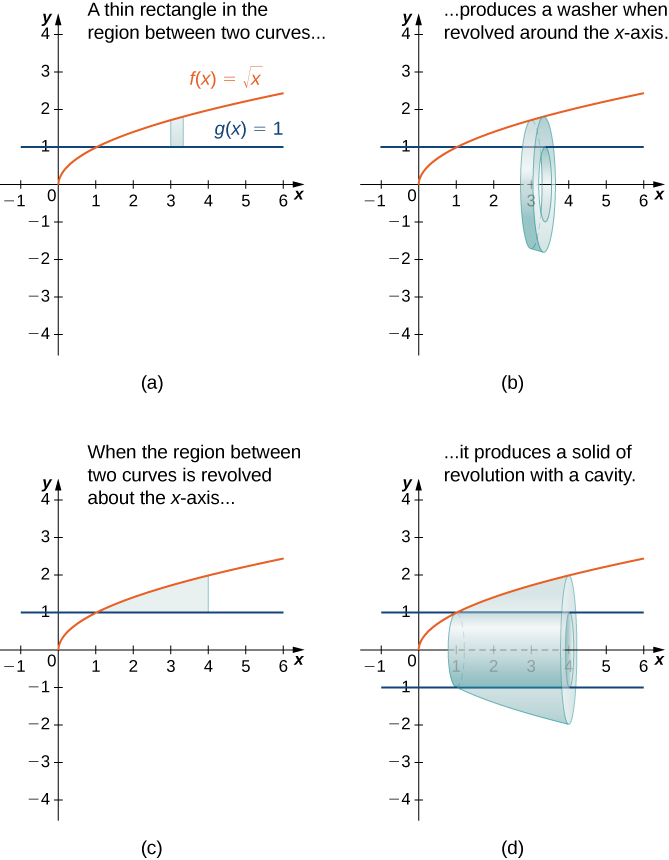
A region between two curves is sliced by a thin rectangle, which becomes a washer when revolved about the -axis. The four panels illustrate the region, a washer slice, the full bounded region, and the resulting solid. The functions and interval shown are specific examples that extend beyond the general syllabus but effectively demonstrate the washer construction. Source.
Identifying Outer and Inner Radii from Graphs
A diagram typically includes two curves, such as y=f(x) and y=g(x), along with a specified axis of revolution. The visual layout determines which curve is farther from the axis at each point in the interval. The outer radius is always the larger distance between a boundary curve and the axis, and the inner radius is the smaller distance.
Outer Radius: The distance from the axis of revolution to the farther boundary curve that determines the outer boundary of each washer.
This distinction is crucial because the washer method depends on subtracting the inner circular area from the outer circular area to obtain the ring-shaped slice.
A diagram also allows students to recognize when the relative positions of curves shift. For instance, a curve that forms the outer boundary over part of the interval may become the inner boundary elsewhere, requiring careful attention to graph intersections. These positional changes must be seen clearly to avoid applying incorrect radii over a region.
Understanding the Generated Solid Through Visualization
The washer method is fundamentally about accumulation: summing infinitely many circular slices to form a three-dimensional solid. Graphs and diagrams show how these slices stack and how their radii vary across the interval. The revolved region can appear simple or complex, but its shape becomes easier to interpret when the diagram makes clear the distance relationships.
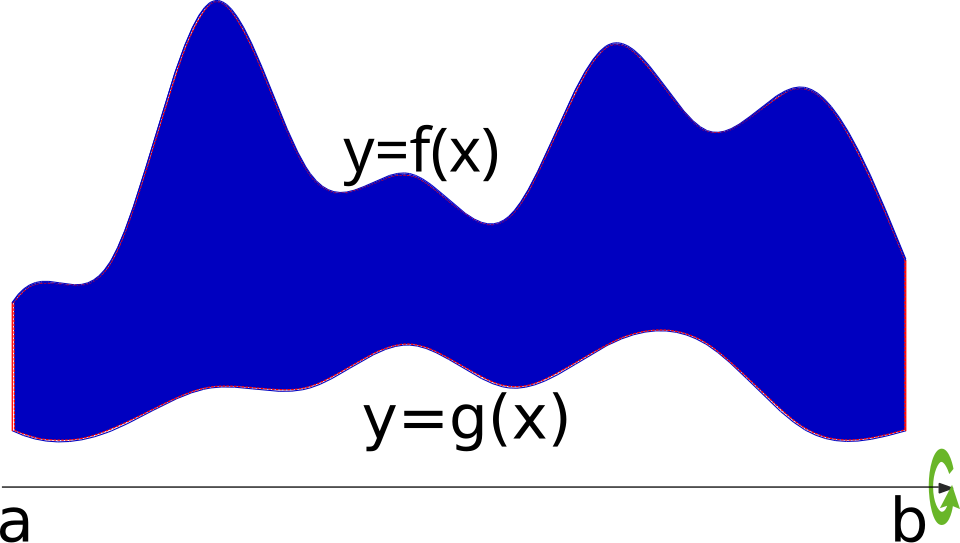
A shaded planar region appears beside an axis of revolution, with the corresponding solid of revolution sketched on the opposite side. The image highlights the connection between the two-dimensional region and the three-dimensional form it generates. The specific curves included provide additional detail beyond the syllabus but still illustrate the general washer geometry. Source.
Inner Radius: The distance from the axis of revolution to the closer boundary curve that forms the hole in the washer.
After identifying radii, students translate the visual information into a definite integral that captures the volume of all washers. Recognizing how a vertical or horizontal slice sweeps out a ring when revolved depends on noticing orientation. If slicing perpendicular to the axis, the variable of integration must match the slice direction, and the radii must be measured consistently in that orientation.
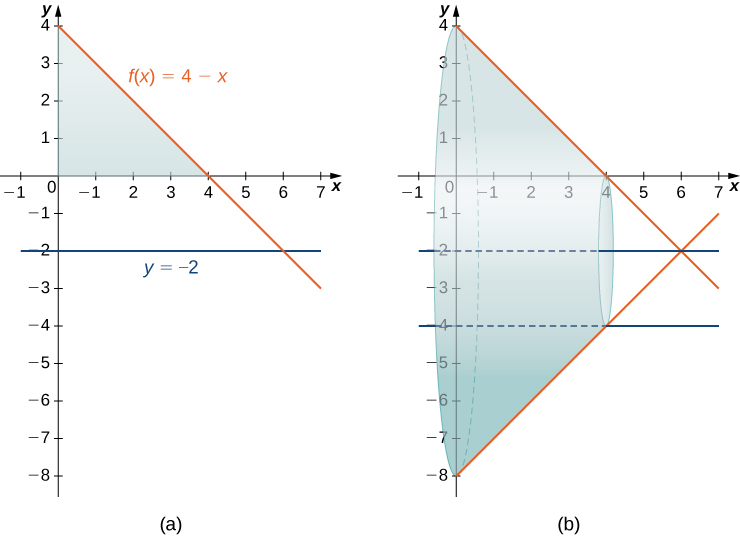
The diagram shows a triangular region under over and the solid formed by revolving it about . Outer and inner radii appear as distances from this shifted axis rather than the standard axes. The specific functions provide contextual detail beyond the syllabus but clearly illustrate washer geometry around a nonstandard axis. Source.
Expressing Radii and Setting Up the Volume Integral
Once diagrams reveal radius relationships, the washer volume is represented using the standard formula.
V(x) = π[(R(x))² − (r(x))²]
R(x) = Outer radius measured from the axis of revolution
r(x) = Inner radius measured from the axis of revolution
A single sentence separating equation blocks ensures that students understand that formulas follow directly from the meaning of circular areas.
Graphs often show whether radii should be written in terms of x or y, depending on how the region is oriented and how the washers stack. If washers stack along the horizontal direction, radii must be expressed using functions of x; if they stack vertically, functions of y are required instead. Diagrams guide this decision by highlighting the direction in which slices naturally form.
Using Intersection Points in Diagram-Based Interpretation
Intersections determine where the outer and inner radii may switch roles. Visualizing these points ensures the integral covers only the region that truly generates washers. Without this, a student might apply one radius expression across an interval where the curves actually change order. Diagrams make these transitions clear by showing where curves cross and how their distances to the axis change.
Accurate interpretation of these graphical features directly supports the syllabus expectation that students use diagrams to see how the solid forms, how radii arise, and how the washer method expresses volume as accumulated ring-shaped slices.
FAQ
If the diagram shows a region that does not touch the axis of revolution, a hollow space will form when it is revolved, indicating washers rather than discs.
Look for a visible gap between the region and the axis; if the boundary curve never reaches the axis, an inner radius will exist.
If the region touches the axis anywhere in the interval of revolution, discs may appear on that subinterval instead.
Changes usually occur where the curves intersect or where one curve switches from being farther from the axis to being closer.
Useful cues include:
• Intersection points marked or labelled on the graph.
• A curve bending or crossing the axis of revolution.
• A shaded region that appears to shift vertically or horizontally relative to the axis.
These suggest the need to split the integral into subintervals.
Look at the direction of the representative slice shown or implied by the diagram.
Vertical slices produce radii measured vertically and typically require integration with respect to x.
Horizontal slices produce radii measured horizontally and usually require integration with respect to y.
Diagrams with clearly drawn slices, shaded strips, or directional arrows are especially helpful for choosing the correct orientation.
Typical mistakes arise from reading distances incorrectly in relation to the axis.
Common issues include:
• Using the difference between two functions as a radius without referencing the axis.
• Misreading vertical distances as horizontal ones (or vice versa).
• Assuming the top curve is always the outer radius even if the axis is not horizontal.
Carefully tracing each radius directly back to the axis avoids these errors.
Diagrams often show the axis drawn clearly above, below, or beside the region, illustrating that radii extend across the empty space between the region and the axis.
To interpret this correctly:
• Identify the region’s boundary and locate the axis.
• Observe any visible gap indicating that radius lengths include that extra distance.
• Note whether the axis lies within the region, which would alter or eliminate the inner radius.
These visual relationships ensure radii are measured accurately.
Practice Questions
Question 1 (1–3 marks)
A region in the xy-plane is bounded above by the curve y = 5 − x and below by the x-axis. The region is revolved about the x-axis, forming washers. State which function determines the outer radius of the washers and give a reason based on the graph.
Question 1 (1–3 marks)
• 1 mark for identifying the outer radius as the distance from the x-axis to the curve y = 5 − x.
• 1 mark for correctly stating that y = 5 − x lies above the x-axis on the interval shown.
• 1 mark for a clear explanation that the outer radius is determined by the curve farthest from the axis of revolution.
Question 2 (4–6 marks)
The region bounded by y = 4x, y = 0, and x = 2 is revolved about the horizontal line y = −3.
(a) Write an expression for the outer radius in terms of x.
(b) Write an expression for the inner radius in terms of x.
(c) Using your radii, write the definite integral that represents the volume of the resulting solid using the washer method (do not evaluate).
Question 2 (4–6 marks)
• 1 mark for correctly expressing the outer radius as the distance from y = −3 to the curve y = 4x (outer radius = 4x − (−3) = 4x + 3).
• 1 mark for correctly expressing the inner radius as the distance from y = −3 to y = 0 (inner radius = 0 − (−3) = 3).
• 1 mark for recognising that washers are used because the solid has a hole.
• 1–3 marks for a correct definite integral for the volume of the solid:
Integral from x = 0 to x = 2 of pi[(outer radius)² − (inner radius)²] dx.

