Understanding Arc Length as Accumulated Change in Position

Arc length in AP Calculus AB (BC-only extension) describes how the total length of a smooth curve can be understood as the accumulation of infinitesimal changes in position, represented through a definite integral. These ideas build on students’ understanding of integration as summing infinitely many small contributions.

Arc length focuses on viewing a curve not just as a graph but as a path along which position changes continuously. Because a curve captures movement in both horizontal and vertical directions, its total length cannot be found using a simple subtraction of coordinates; instead, it requires integrating small changes that together form the entire distance traveled.

Small Changes in Position Along a Curve

A planar curve defined by a differentiable function changes position in a way that can be approximated by very small linear segments. Each segment reflects how the function moves in the plane over a tiny interval of its domain.

When we consider sufficiently small pieces of a curve, each piece behaves almost like a straight line. This idea allows us to measure curve length by summing the lengths of many very small line segments.

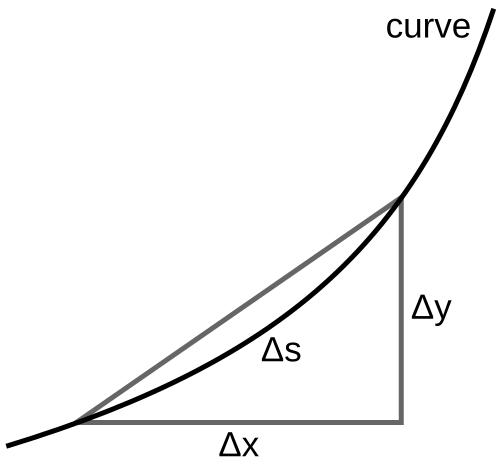
A smooth curve is divided into tiny pieces, each approximated by a straight segment with length $\Delta s$. The horizontal change $\Delta x$ and vertical change $\Delta y$ combine through the Pythagorean theorem to determine $\Delta s$. This visualization shows how summing these segment lengths leads to the definition of arc length as accumulated change in position. Source.

Infinitesimal Change and Smoothness

A curve suitable for arc length must be smooth, meaning its derivative exists and does not exhibit sudden jumps or corners. Smoothness ensures that the direction of the curve changes gradually, enabling the use of integration for measuring its length.

Smoothness also guarantees that the curve behaves predictably over small intervals, making the accumulation approach appropriate for defining total length.

Arc Length as Accumulation

To measure arc length, calculus treats the curve as being composed of infinitely many segments. Each segment represents a tiny change in position. These changes combine through integration to produce the exact length of the curve across the given interval.

Because arc length depends on how steeply a function rises or falls, the derivative plays a central role; it reflects the curve’s instantaneous rate of change. Steeper slopes create longer distances over the same horizontal movement.

This integral accumulates the lengths of infinitely many small linear approximations, each capturing both horizontal and vertical components of movement.

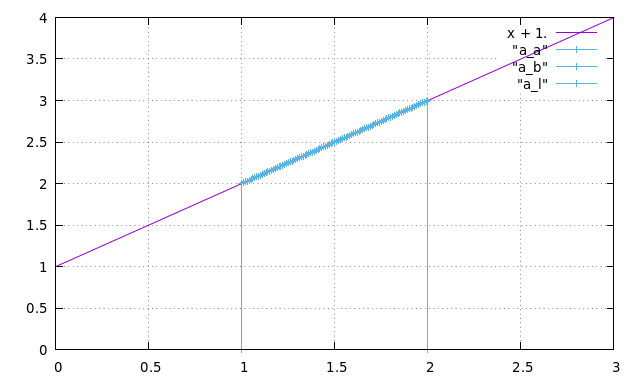
The graph of $f(x)=x+1$ over a closed interval is shown together with the arc length integral $\int_a^b \sqrt{1+(f'(x))^2},dx$. The constant slope $f'(x)=1$ makes the integrand constant, yet the arc length still requires integration to accumulate total distance. This figure demonstrates how the analytic arc length formula corresponds to geometric change in position along a graph. Source.

A sentence separating blocks helps reinforce that the integral emerges naturally from geometrical reasoning.

Why the Derivative Appears in Arc Length

The derivative quantifies how much the function changes vertically for a small horizontal change. This information combines with horizontal movement to determine the slant of each tiny segment. Because the curve’s steepness varies along its domain, the derivative ensures the accumulated length reflects each part’s true geometric contribution.

Interpreting Arc Length Through Motion

Arc length can also be understood through the lens of motion, where the curve represents a path and position changes continuously as a variable moves along the domain. In this view:

• The horizontal axis represents a parameter such as time or input value.

• The curve describes how position in the plane evolves.

• The definite integral of arc length expresses the total distance traveled along this path.

This interpretation aligns with the syllabus statement that arc length represents “accumulation of small changes in position.”

Key Ideas for Visualizing Accumulated Length

Arc length relies on geometric and analytical reasoning working together. The following points support student understanding:

• A curve is approximated by many small line segments. Each segment represents a nearly linear piece of the curve.

• The length of each small segment involves both horizontal and vertical change. These combine through the Pythagorean relationship embedded in the arc length formula.

• Integration sums infinitely many contributions. This accumulation produces an exact value, not an approximation.

• Smoothness guarantees reliability. The derivative must remain well-behaved on the interval so the integral accurately reflects the curve.

How Accumulation Reflects Movement in the Plane

Accumulation is central to understanding arc length because distance is inherently additive. Each tiny segment contributes some amount of length, and the integral ensures all contributions—no matter how small—are included. This process quantitatively captures the intuitive idea of tracing a curve from point $a$ to point $b$ with perfect precision.

Situating Arc Length in the Context of AP Calculus

Although arc length is a BC-only topic, it reinforces essential AP Calculus principles:

• The view of definite integrals as accumulated change.

• The use of derivatives to represent instantaneous behavior.

• The extension of integration beyond area to measure geometric quantities.

• The interpretation of mathematical expressions as representing real, measurable features of curves.