The arc length of a smooth curve represents how far a point travels along its path, and definite integrals allow us to accumulate infinitesimal changes in position precisely.

Understanding Arc Length as an Accumulated Quantity

Arc length extends the idea of measuring straight-line distance to measuring distance along a smooth planar curve, where the path may bend continuously. Because the curve is not composed of straight segments, distance is obtained by summing extremely small linear pieces that approximate the curve’s behavior over tiny intervals. This process reflects the syllabus emphasis on an appropriate definite integral expression used to compute the length over a specified domain.

A smooth curve in AP Calculus AB is typically described by a differentiable function whose derivative does not exhibit jumps or corners. This smoothness ensures that its local rate of change can be used to construct the integral expression for length.

The Arc Length Formula for a Function $y=f(x)$

To quantify how distance accumulates along a curve, we approximate infinitesimal segments of the curve using right triangles, where each triangle’s hypotenuse represents a tiny portion of the path.

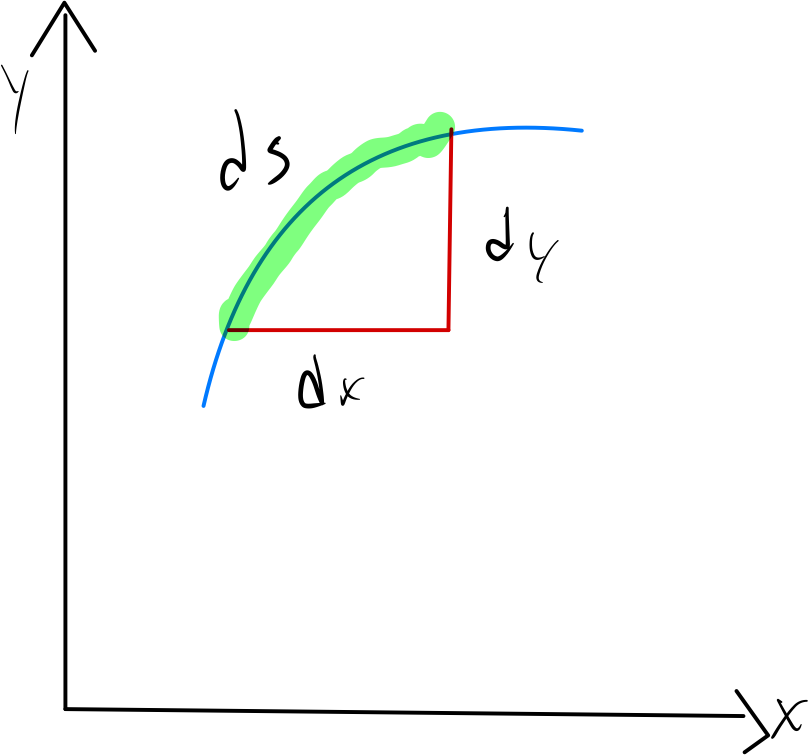
A smooth planar curve between two nearby points is approximated by a right triangle with horizontal change $dx$, vertical change $dy$, and arc length $ds$ along the curve. This geometry leads to the relation $ds = \sqrt{dx^2 + dy^2}$, which underpins the arc length integral. The diagram focuses purely on the local behavior of the curve and does not introduce extra topics beyond the AP Calculus AB arc length syllabus. Source.

Because the integrand involves a square root of an expression containing $f'(x)$, the resulting integral often cannot be evaluated using elementary antiderivatives. However, the purpose of this subsubtopic is not to emphasize evaluation techniques but rather the correct setup and conceptual understanding of how the integral expresses accumulated distance.

Conditions for Using the Arc Length Integral

The formula above applies when the curve is smooth, meaning the derivative exists and is continuous over the interval. This smoothness ensures that the small hypotenuse segments used in the derivation accurately reflect the curve’s behavior. When these conditions hold, the definite integral directly represents the sum of all infinitesimal distances between nearby points along the curve.

The integral’s structure also guarantees that the integrand remains nonnegative, since distances must accumulate positively regardless of whether the function increases or decreases.

Interpreting the Components of the Arc Length Expression

Each part of the integrand corresponds to a geometric interpretation grounded in the Pythagorean theorem.

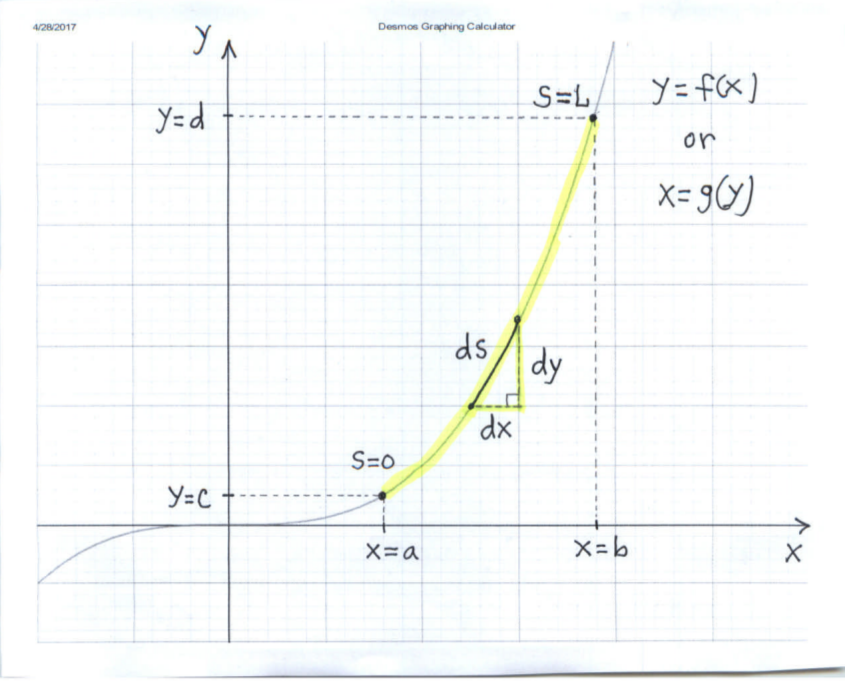
This graph shows a smooth curve $y=f(x)$ from $x=a$ to $x=b$, with the arc length parameter $s$ running from $0$ to $L$. A small segment of the curve is magnified as a right triangle with base $dx$, height $dy$, and hypotenuse $ds$, illustrating how $ds$ is built from horizontal and vertical changes. The labels $y=c$, $y=d$, and “$x=g(y)$” slightly exceed the AB syllabus but reflect the same geometric structure underlying arc length. Source.

For students, recognizing how the slope contributes to arc length reinforces the idea that curves become “longer” where they turn sharply and “shorter” where they remain nearly horizontal. The definite integral then accumulates all these local contributions to provide the total length.

A smooth curve can be steep in some regions and nearly flat in others, and the arc length integral adapts seamlessly to these variations.

Why Definite Integrals Are Essential for Arc Length

The syllabus emphasizes that an appropriate definite integral expression is used to find arc length. This is because a definite integral is uniquely suited to accumulate infinitely many pieces of infinitesimal information. In the arc length context, these pieces represent tiny distances, each derived from the function’s differential structure.

Between definition blocks, it is important to understand that the definite integral is not merely symbolic; it stems from geometric reasoning about distances in the plane.

Interpreting Arc Length in Applied and Geometric Contexts

Arc length calculations arise when a quantity depends on the exact distance traveled along a curve rather than straight-line displacement. For instance, the path of a particle or the length of a wire shaped as a smooth graph requires the accumulated distance along that graph. This subsubtopic focuses specifically on using the integral expression, not on modeling or real-world interpretation, but the meaning of arc length remains grounded in accumulated position change.

The requirement that the curve be planar indicates that all measurements occur in the two-dimensional coordinate system, with no additional geometric complexity.

Structuring Arc Length Computations in AP Calculus AB

In AP Calculus AB, the primary objective for this subsubtopic is:

• Identify when a curve is given by a differentiable function $y=f(x)$.

• Confirm that the function is smooth on the specified interval.

• Compute or set up $f'(x)$ and substitute it into the arc length integrand.

• Express the arc length using the definite integral from $a$ to $b$.

• Interpret the integral as an accumulated distance along the curve.

These steps reflect the balance between conceptual understanding and proper mathematical expression expected at this level.

Though closed-form antiderivatives may not exist for many arc length integrals, proper setup demonstrates mastery of the topic and aligns with the syllabus focus on selecting and using the appropriate definite integral expression for the curve’s length over a domain.