Area Between Two Functions of x (8.4.2) | AP Calculus AB Notes

AP Syllabus focus:
‘The area of a region between two functions of x on [a,b] is found with a definite integral of the difference, ∫_a^b (top function − bottom function) dx.’

The area between two functions of x is determined by interpreting the vertical difference between them as accumulated rectangular slices, enabling precise measurement of enclosed regions using integration.

Area Between Two Functions of x

Determining the area between two functions of x is an essential skill in integral calculus and one that relies on understanding how vertical distances accumulate across an interval. When two curves bound a region, the definite integral provides an exact measure of that enclosed area by summing infinitely many thin slices whose heights represent differences between function values.

Understanding Vertical Distance Between Curves

When two functions, written as $y=f(x)$ and $y=g(x)$ , describe the upper and lower boundaries of a region on an interval, the vertical separation of the curves at each value of $x$ represents the height of a rectangular slice. The area is accumulated by integrating this vertical distance across the domain where the functions enclose the region.

In this context, the phrase top function refers to the function with the greater $y$ -value on the interval, while the bottom function refers to the function with the lesser $y$ -value. Identifying these roles is essential because the area formula subtracts the bottom value from the top value to ensure a nonnegative slice height.

When the bottom function is the x-axis, the area is just the area under a single graph, which is a special case of the area-between-curves formula.

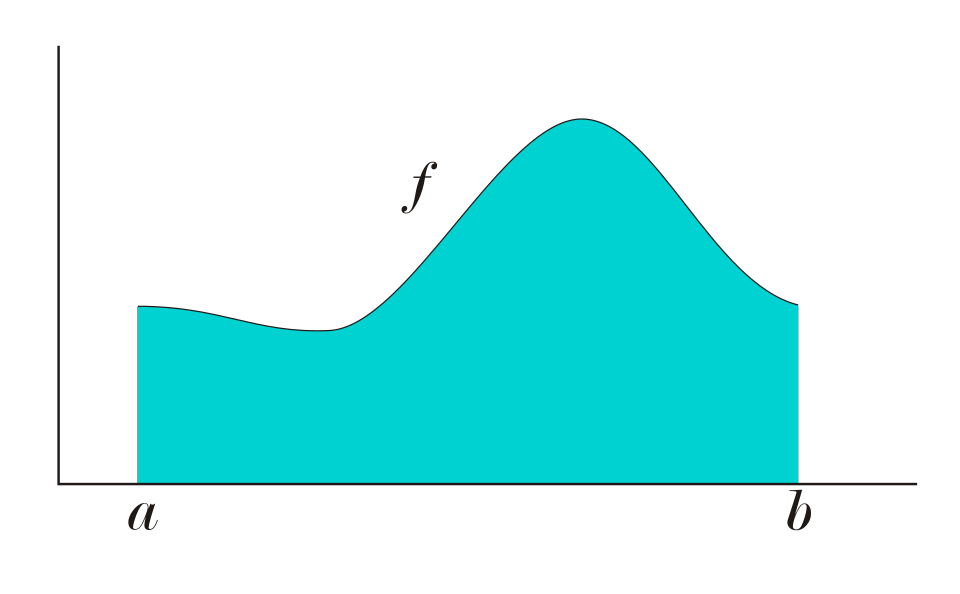
This graph shows a positive function with the region under its curve between $x=a$ and $x=b$ shaded to represent the definite integral. The shaded area corresponds to $\int_a^b f(x),dx$ , which can be interpreted as the area between the curve $y=f(x)$ and the x-axis. In the context of area between curves, this is the special case where the bottom function is $y=0$ . Source.

The Integral Structure of Area Between Curves

The definite integral serves as the tool for accumulating infinitely many slices of equal infinitesimal width and varying height. For AP Calculus AB students, this relationship is expressed with a precise and widely used formula.

$A = \int_a^b \big( f_{\text{top}}(x) - f_{\text{bottom}}(x) \big), dx$
$A$ = Area between the curves on the interval; units squared
$f_{\text{top}}(x)$ = Function with greater value on $[a,b]$
$f_{\text{bottom}}(x)$ = Function with lesser value on $[a,b]$
$a, b$ = Interval endpoints

This formulation reflects that area is inherently positive. By designating a top and bottom function, the integrand remains nonnegative across the interval of integration. The definite integral accumulates the vertical distances, producing a total area measurement aligned with geometric intuition.

When two curves intersect at the endpoints or within the interval, those intersection points may serve as the limits of integration or guide the identification of correct top and bottom functions.

Identifying Top and Bottom Functions Across an Interval

To use the area formula correctly, students must determine which function lies above the other on the interval. This process involves:

Checking values of each function at test points within the interval.
Considering the graphs of both curves if provided.
Using algebraic reasoning, such as evaluating inequalities between $f(x)$ and $g(x)$ .

Because errors in these identifications change the sign of the integrand, careful analysis is required before setting up the integral. This step ensures that the integrand reflects the vertical thickness of the region at every position between $a$ and $b$ .

Once the correct top and bottom functions are established, the area between the curves is determined by integrating their difference.

Essential Characteristics of the Area Formula

The formula for area between curves expresses several core ideas emphasized in the AP Calculus AB curriculum:

Accumulation of differences: The definite integral measures accumulated vertical distances.
Dependence on function ordering: The subtraction operation requires knowing which curve is higher.
Application on a closed interval: The area is always computed across a specified domain $[a,b]$ .
Geometric interpretation: Each term in the integrand represents the height of a thin vertical slice.

These ideas combine to give students a robust understanding of how integrals translate geometric and graphical properties into quantitative results.

Step-by-Step Structure for Setting Up an Area Integral

Students typically approach area-between-curves problems using a clear, repeatable structure:

Identify the interval where the region is bounded in the $x$ -direction.
Determine which function is on top and which is on the bottom on that interval.
Write the integrand as the difference:
- top function minus bottom function.
Set the limits of integration using the interval boundaries or intersection points.
Integrate the expression to find the area.

Conceptually, the definite integral adds up the areas of infinitely many thin vertical slices, each with height given by the difference between the top and bottom functions.

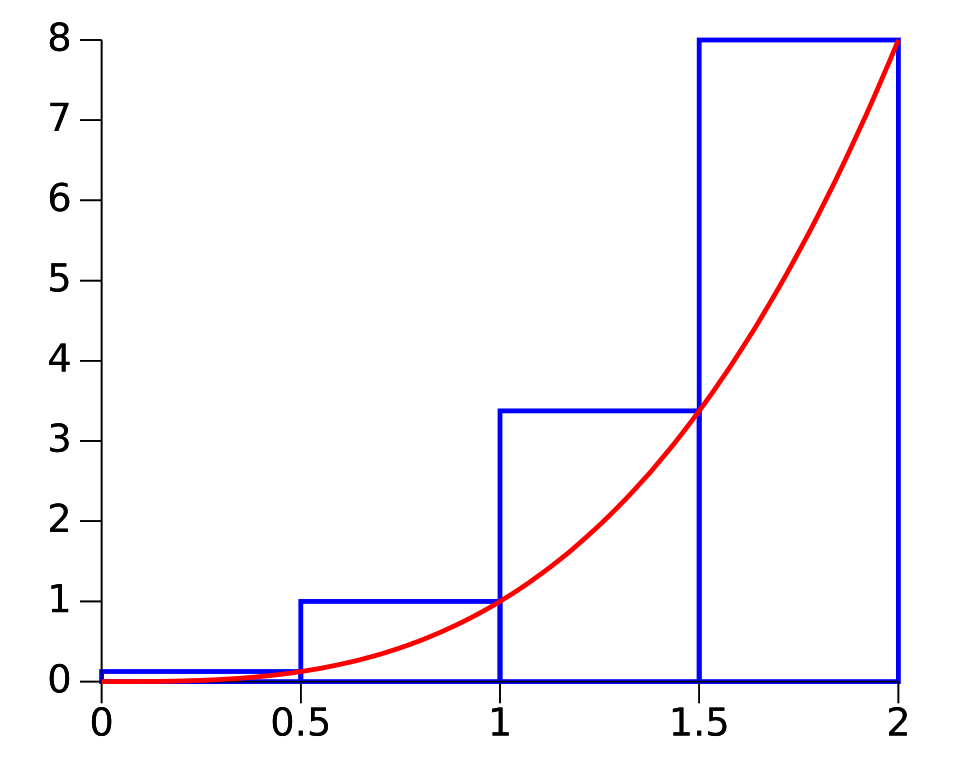
This diagram shows a curve $y=x^3$ over the interval $[0,2]$ with four blue rectangles forming a right Riemann sum. Each rectangle’s height is taken from the function value at the right edge of its subinterval, illustrating how sums of rectangle areas approximate $\int_0^2 x^3,dx$ . Although the picture uses a single top function and the x-axis as the baseline, the same idea extends to rectangles whose heights are $\text{top} - \text{bottom}$ for area between two curves. Source.

Interpreting the Integral Geometrically

Viewing the integral as the sum of infinitely many thin vertical slices reinforces the conceptual link between geometry and accumulation. Each slice:

Has a width of $dx$
Has a height equal to the vertical difference $f_{\text{top}}(x) - f_{\text{bottom}}(x)$
Represents a tiny rectangle whose area contributes to the full region’s area

Through integration, these infinitesimal rectangles are aggregated, revealing the total enclosed area. This perspective ties directly to the syllabus statement that the area between two functions on an interval is found using the definite integral of their difference.

The definite integral $\int_a^b (\text{top function} - \text{bottom function}),dx$ represents the total vertical gap between two graphs over the interval $[a,b]$ .

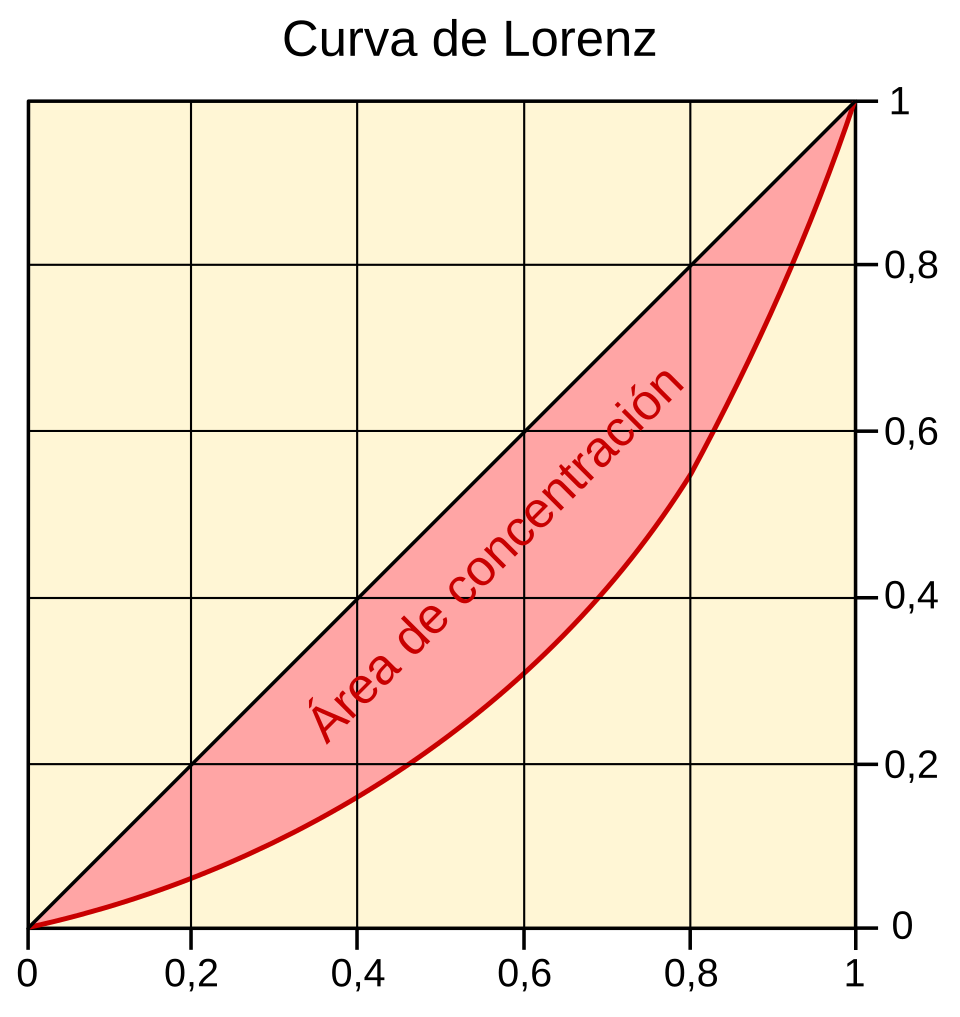
This figure shows two curves on the same axes: a straight “line of equality” and a bowed Lorenz curve, with the region between them shaded. Geometrically, the shaded region represents the area between two graphs, just as in $\int_a^b (\text{top} - \text{bottom}),dx$ . The specific economic interpretation goes beyond the AP Calculus AB syllabus, but the picture clearly illustrates the geometric idea of area between curves. Source.

Relevance to the AP Curriculum

This subsubtopic is a cornerstone of applications of integration. Students use this technique in pure geometric settings and in modeling contexts where two functions represent physical quantities. Mastery of the process prepares students to analyze more complex regions and supports later study of volumes, accumulation functions, and applied modeling with integrals.

FAQ

If the intersection points are not provided, you must find them by solving the equation f(x) = g(x). These solutions give the x-values where the graphs meet and define the boundaries of the region.

If the curves meet more than twice, check which pair of intersections encloses the specific region described in the question. A quick sketch helps avoid selecting the incorrect interval.

If the graphs cross within the interval, the top function may change. You cannot use a single integral if the ordering reverses.

Instead:
• Identify where the crossing occurs.
• Split the integral at the crossing point.
• Use the appropriate top minus bottom function on each subinterval.

This guarantees that each integrand represents a non-negative vertical distance.

Yes, but only when the difference f(x) − g(x) changes sign in a manageable way. Integrating the absolute value ensures all vertical distances are taken as positive.

However, absolute value integrals can be harder to evaluate algebraically, so splitting the integral is often clearer and reduces the risk of errors in sign.

No, the area between two curves depends only on the vertical separation between them, not their position relative to the x-axis.

Even if both functions are negative, the area is still found by subtracting the lower graph from the upper graph. The only time the x-axis matters is when it acts as one of the bounding curves.

A useful habit is to test a single point within the interval. At that x-value:

• Compute f(x) and g(x).
• Check that f(x) − g(x) is positive when f is the top function.
• If the result is negative, you have likely reversed the order of subtraction.

This simple check prevents wasted time evaluating an incorrect integral.

Practice Questions

Question 1 (1–3 marks)
The curves y = 5 − x and y = x − 1 intersect at x = 3.
Find the area of the region bounded by the two curves on the interval 1 ≤ x ≤ 3.

Question 1 (Total: 3 marks)
• 1 mark: Correct identification of top and bottom functions on 1 ≤ x ≤ 3 (top: 5 − x, bottom: x − 1).
• 1 mark: Correct set-up of the integral for area: integral from 1 to 3 of (5 − x) − (x − 1).
• 1 mark: Correct evaluation of area = 4.

Question 2 (4–6 marks)
Let f(x) = x^2 + 2 and g(x) = 6 − x.
(a) Determine the x-values at which f and g intersect.
(b) On the interval between these intersection points, identify which function lies above the other.
(c) Hence calculate the area enclosed between the two curves.

Question 2 (Total: 6 marks)
• 1 mark: Setting f(x) = g(x) to find intersection: x^2 + 2 = 6 − x.
• 1 mark: Solving correctly for x-values: x = −3 and x = 1.
• 1 mark: Correctly identifying the top function on the interval (g(x) = 6 − x above f(x) = x^2 + 2).
• 1 mark: Correct set-up of the area integral: integral from −3 to 1 of (6 − x) − (x^2 + 2).
• 2 marks: Correct evaluation of the integral giving area = 32.

Try All Topic Practice Questions

Written by:

Dr Rahil Sachak-Patwa

Oxford University - PhD Mathematics

Rahil spent ten years working as private tutor, teaching students for GCSEs, A-Levels, and university admissions. During his PhD he published papers on modelling infectious disease epidemics and was a tutor to undergraduate and masters students for mathematics courses.