AP Syllabus focus:
‘Definite integrals for areas between curves are used to model applied problems where a quantity is represented as the vertical difference between two graphs.’
Applied area problems use definite integrals to represent real quantities by interpreting vertical differences between functions as measurable amounts accumulated across an interval.
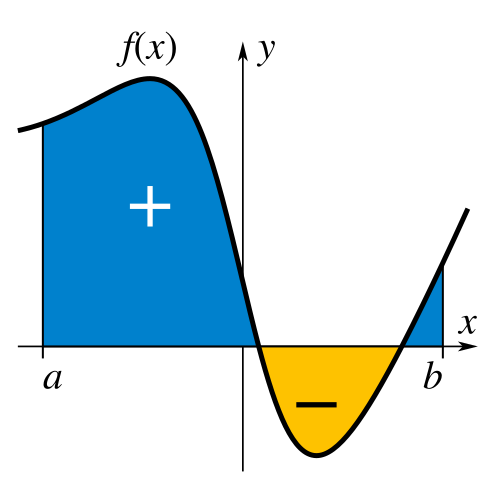
This diagram illustrates a definite integral as the shaded region under a function between two points on the x-axis, and . The shaded region represents the accumulated value of the rate given by the function across the interval. Although the figure includes both positive and negative shaded regions, only the fundamental idea of area as accumulated quantity is required for this subsubtopic. Source.
Understanding Applied Area Problems Using Functions of x
Applied area problems involve identifying a real-world or contextual quantity that can be expressed as the vertical distance between two functions on an interval. This distance, when accumulated through integration, produces an area that corresponds to a meaningful measure in context. The approach extends the core idea that the area between two curves on is found by integrating the top function minus the bottom function, but applied situations require interpreting the resulting area in terms of physical, economic, biological, or other contextual quantities.
When problems are framed in applied settings, students must translate context into mathematical structure by recognizing how the graphs represent varying quantities and how integration captures the total accumulated effect over the specified interval.
Identifying Top and Bottom Functions in Context
Recognizing Graphical Meaning
In an applied setting, the top function is the one whose value lies above the other at each input within the relevant interval. The bottom function lies below it. This vertical hierarchy represents differences such as production minus cost, inflow minus outflow, or upper boundary minus lower boundary of a physical region.
Top Function: The function in an applied area problem whose graph lies above the other function on the interval used to compute the area.
This distinction is essential because the integral of the difference must remain nonnegative to accurately represent an area or accumulated amount.
Typical Applied Interpretations
Common scenarios include:
Net accumulation of a spatial quantity (e.g., height differences forming a physical region).
Differences between two varying rates or levels, such as revenue minus cost.
Representing a physical region in terms of upper and lower boundaries.
These contexts all rely on the consistent interpretation of vertical distance as the amount being accumulated.
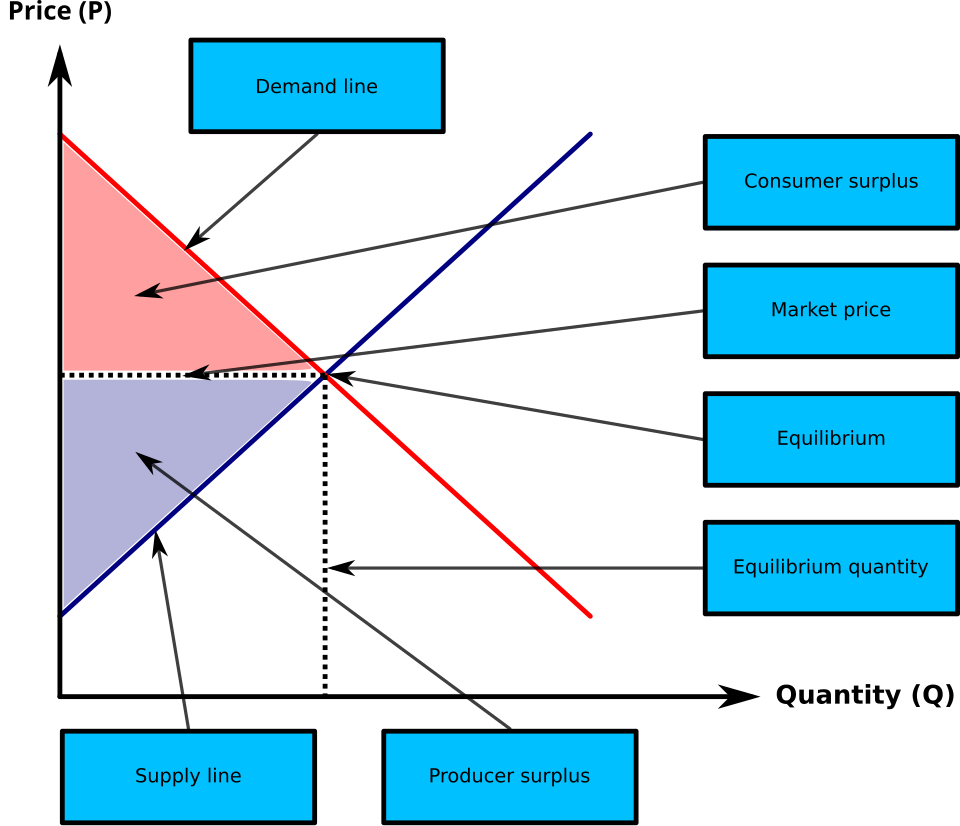
This graph shows demand and supply curves with shaded regions representing consumer and producer surplus. Each shaded region is an area between curves, interpreted as an accumulated economic quantity across all units. The presence of both surplus regions introduces extra economic context beyond the calculus syllabus, but the essential idea is the vertical difference between functions. Source.
Setting Up the Definite Integral for Applied Areas
Translating Applied Descriptions
To formulate an area integral, students translate verbal descriptions into mathematical expressions by identifying:
The interval that defines the domain of the region or time period.
The two functions describing the boundaries.
Which function represents the upper boundary and which represents the lower boundary.
= Accumulated area or contextual quantity
= Top function providing the upper boundary
= Bottom function providing the lower boundary
= Interval endpoints for accumulation
Applied interpretations require viewing this integral not simply as geometric area but as total accumulated quantity across the input interval.
Students must identify correct limits based on contextual cues, such as time windows, location boundaries, or intersection points stated or implied in the problem.
Interpreting the Integral in Applied Contexts
Understanding Accumulated Quantities
In applied problems, the definite integral measures how much of a selected quantity accumulates over an interval. The amount accumulated at each point is represented by the instantaneous vertical difference between the two functions. Integrating this difference compiles the contributions from infinitely many small slices.
Accumulated Quantity: The total amount represented by summing contributions of a quantity across an interval, computed using a definite integral.
Between definition blocks, it is important to emphasize that interpretation depends entirely on the real-world meaning assigned to the functions.
Types of Applied Interpretations
Students may encounter situations where the area corresponds to:
Physical size, such as land areas bounded by functional curves.
Economic totals, such as accumulated profit constructed from vertical differences between revenue and cost graphs.
Environmental or biological measures, such as differences between two growth-related functions.
Engineering or physics quantities, such as displacement differences represented graphically.
Each requires understanding that the vertical separation directly encodes the amount per unit input, and integration produces the total.
Analyzing Applied Problems Graphically and Verbally
Using Graphs
Graphs help students visualize which function lies above the other. Important steps include:
Locating intersection points whenever the curves meet.
Determining the ordering of the functions on each subinterval.
Verifying that the top function remains above the bottom function across the domain.
Using Descriptive Information
Verbal descriptions may specify contextual boundaries that determine the integration interval. Students must:
Interpret phrases like “between time and ,” “over the length of the beam,” or “across the region bounded by…”
Translate descriptive boundaries into a closed interval for integration.
Identify which function represents the greater level or quantity at each input.
Process for Solving Applied Area Problems
Students can approach applied area problems by following a clear process that ensures accurate translation from context to mathematics:
Determine the relevant interval based on contextual cues or stated boundaries.
Identify the two functions that define the quantity’s upper and lower limits.
Decide which function is top and which is bottom on the interval.
Express the accumulated quantity using the definite integral of their difference.
Interpret the definite integral’s result entirely in terms of the applied situation.
Applied area problems reinforce that simply calculating an integral is not enough; the value must be understood as a meaningful, context-dependent quantity representing accumulated difference between two varying levels.
FAQ
The meaning depends entirely on what the functions represent in the real context. If the functions describe physical boundaries, the integral gives a geometric area.
If the functions describe varying levels of a quantity such as cost, temperature, or concentration, the integral represents the total accumulated difference, not a physical region.
Always check the units of each function and the input variable to guide interpretation.
You must determine whether the curves intersect by analysing the functions or their graphs.
If they swap positions, split the interval at each intersection point.
Then integrate top minus bottom separately on each subinterval to ensure the accumulated quantity remains meaningful and non-negative.
Continuity ensures that no sudden jumps or breaks occur, making the vertical difference well-defined everywhere.
It also guarantees that the definite integral exists over the entire interval.
If functions are not continuous, you may need to break the interval at discontinuities and interpret each section separately.
Look for consistent trends: one function may always exceed the other in value even when the curves appear visually close.
Check labelled tick marks to compare specific values.
Trace both functions at key points—start, end, and mid-interval—to confirm which lies above.
Subtracting two functions must give a quantity with meaningful units, such as metres, dollars, or degrees Celsius.
Integrating that difference multiplies the units by those of the input variable, producing the correct final unit.
If the resulting unit does not match the intended interpretation, the integrand or interval may have been chosen incorrectly.
Practice Questions
Question 1 (1–3 marks)
A company tracks two functions over the time interval 0 ≤ t ≤ 5.
The revenue at time t is given by the function R(t), and the cost at time t is given by the function C(t).
Explain how you would compute the total profit accumulated over the interval 0 ≤ t ≤ 5 using an integral, and state which function must be placed first inside the integrand.
(No evaluation of the integral is required.)
Question 1 (1–3 marks)
• 1 mark: States that the total profit is found by integrating the vertical difference between the revenue and cost functions.
• 1 mark: Identifies that the correct integrand is R(t) − C(t).
• 1 mark: States that the integral is taken over the interval 0 ≤ t ≤ 5.
Question 2 (4–6 marks)
A tank contains two flowing substances.
The height of substance A above the base at position x is modelled by the function f(x), and the height of substance B above the base at the same position is modelled by the function g(x).
On the interval 2 ≤ x ≤ 10, the height of substance A is always greater than the height of substance B.
(a) Write an integral expression for the total area of the vertical cross-section between the surfaces of the two substances on 2 ≤ x ≤ 10.
(b) Interpret the meaning of this area in the real context of the tank.
(c) State one reason why the order of the functions inside the integrand matters in applied problems of this type.
Question 2 (4–6 marks)
• 1 mark: Correctly writes an integral of the form ∫[2 to 10] (f(x) − g(x)) dx.
• 1 mark: Ensures the order f(x) − g(x) reflects that f(x) is above g(x).
• 1 mark: Provides a correct contextual interpretation that the area represents the total vertical separation or total accumulated height difference between the two substances.
• 1 mark: Identifies that the area corresponds to a physically meaningful quantity in the tank (for example, a measure of volume per unit width).
• 1 mark: States that the order of functions matters because a negative value would not represent an area or meaningful physical quantity.
• 1 mark: Gives a second valid reason related to applied interpretation, such as ensuring the difference reflects the correct upper and lower boundaries.

