AP Syllabus focus:
‘To calculate area between curves, students identify where graphs intersect, determine which function is greater on each subinterval, and set up appropriate definite integrals.’
Understanding how to use graphs and intersection points to construct area integrals is essential because graphical relationships reveal which function dominates each interval, ensuring accurate representation of accumulated area.
Using Graphical Information to Determine Regions
Graphical analysis is central to setting up area problems because the shape, boundaries, and relative position of curves determine how the integral must be written. When working with regions bounded by two functions, students rely on plotted behavior to identify where these functions intersect and how their ordering changes.
Reading Graph Behavior
Graphs show key features needed to construct the correct integral expression:
Points at which functions cross or touch
Intervals on which one function lies above the other
Changes in vertical ordering that require adjusting the integrand
Visual cues for where the region begins and ends
These graphical features guide the choice of bounds and the structure of the integrand, reinforcing the idea that area is accumulated vertical distance over the interval of interest.
Identifying Intersection Points
Intersection points anchor the boundaries of subintervals and frequently serve as the limits of integration. The intersection point between two functions and is the value of at which the two curves produce the same output.
Intersection Point: A value of the input where two functions satisfy , determining boundaries for region separation.
Intersection points may be provided, estimated from a graph, or solved algebraically depending on the information available. Because area between curves depends on the difference between outputs, finding these points ensures the definite integral begins and ends at locations corresponding to genuine geometric boundaries.
A graph typically reveals whether intersections create a single unified region or multiple sections.
From the graph, the intersection points mark the -values that become the limits of integration for the area between the curves.
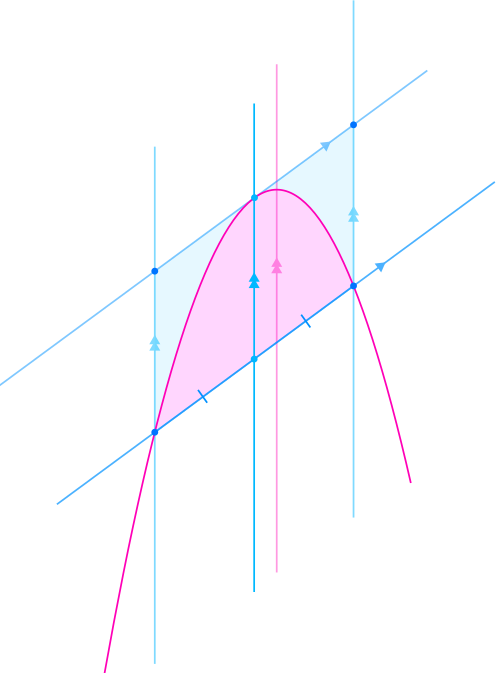
A parabola and a slanted chord define a shaded bounded region, illustrating how intersection points establish the limits of integration when constructing an area-between-curves integral. The specific curves exceed syllabus requirements, but the geometric idea directly supports understanding of bounded regions. Source.
Determining Top and Bottom Functions
Recognizing which function is the top function and which is the bottom function above an interval is essential, because area between curves is always computed in terms of vertical distance.
Top Function: The function with the greater output value on a given interval, defining the upper boundary of the region.
Students use graphs to visually confirm which function lies above the other. Because functions may switch positions, the graph must be reviewed across the entire interval to ensure that a single integrand accurately represents the region.
An interval where the ordering changes cannot use one integrand expression; it must be split into subintervals according to intersection points.
Setting Up the Definite Integral
Once the vertical arrangement of functions and their intersection points are known, the definite integral expressing area can be formed. The general expression uses the difference between the top and bottom functions, integrated across the interval that defines the region.
= Area of the region (square units)
= Intersection points or interval endpoints (units of )
Students must ensure the integrand is always nonnegative, reflecting area as an accumulation of vertical distance. When the graph shows the top and bottom functions changing, the total area is written as the sum of multiple integrals, each with its own integrand corresponding to the correct ordering of functions.
This process emphasizes that the graph dictates the structure, not the algebra alone. Even functions that appear simple symbolically may require multiple integrals when plotted.
Using Intersection Points to Partition the Region
Intersection points divide the region into subintervals, each with consistent vertical ordering. The essential steps are:
Identify all intersection points within the interval of interest.
Divide the overall region into subregions according to these intersection points.
Determine which function is above and which is below on each subregion.
Write a separate definite integral for each portion.
This partitioning process ensures that the integrand always reflects the true geometry of the region and avoids misrepresenting area when curves intersect more than once.
Visual Reasoning for Accurate Integral Construction
Graphs provide immediate insight into qualitative behavior such as steepness, curvature, crossings, or pointwise dominance. When students rely solely on symbolic expressions, they may misinterpret which function forms the top boundary, particularly in intervals where the functions exhibit similar values.
Bullet points for essential visual checks:
Confirm the direction of increasing and the orientation of curves.
Identify whether intersections form closed bounded regions.
Check whether end behavior beyond intersections affects the chosen interval.
Observe whether any portion of the region extends above or below the -axis (though for area between curves this does not affect integrand setup).
Graphs thus serve as the foundation for validating the structure of the integral and preventing common errors such as reversing top and bottom functions or using incorrect bounds.
Interpreting the Region Defined by the Curves
After setting up the integrals, students must ensure the integrals correspond exactly to the graphically defined region. This conceptual connection—area as accumulated vertical separation—is reinforced whenever graphs are used to outline the region’s shape, intersection points form boundaries, and integrals represent the geometric structure precisely as the syllabus describes.
Once the region is identified on the graph, the definite integral represents the accumulation of thin rectangular strips that approximate its area.
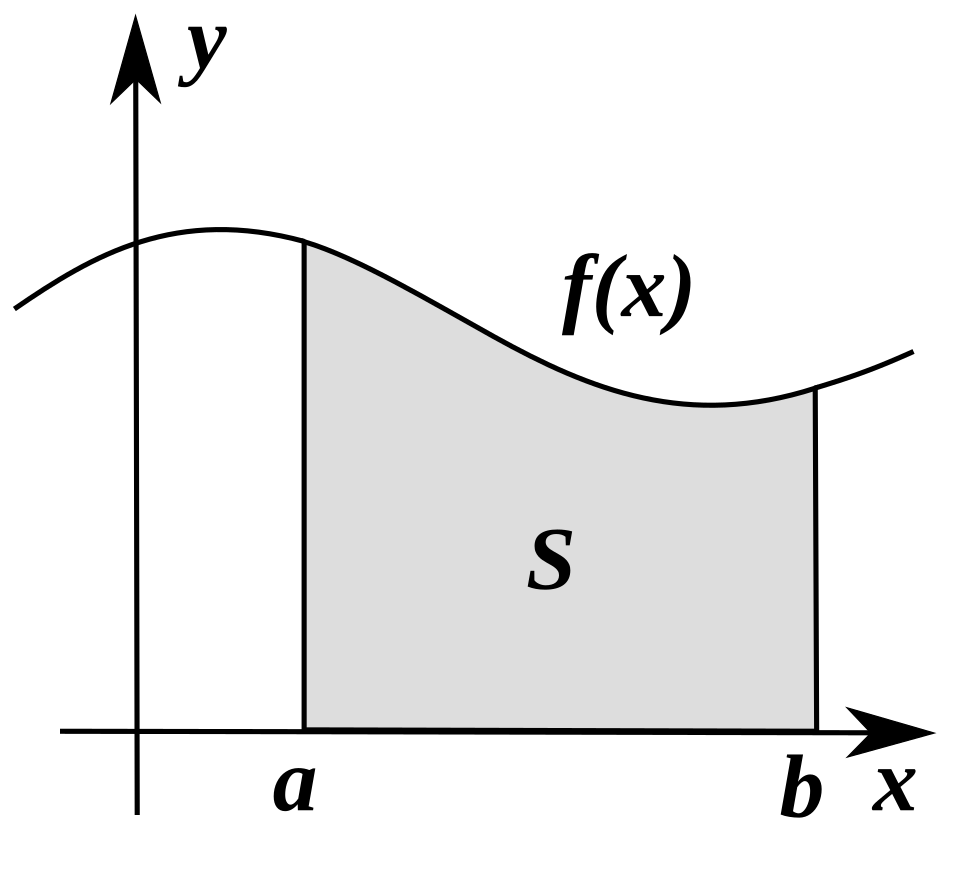
A curve and its shaded subregion illustrate how a definite integral accumulates area through vertical slices, reinforcing the interpretation of area as . Although shown for a single curve, the same slicing concept underlies integrals of “top minus bottom” for area between curves. Source.
FAQ
When an exam diagram is provided, intersection points only need to be read to the level of precision implied by the scale. This may mean integer, half-integer, or one-decimal-place accuracy depending on the axes.
If the graph has no visible scale, the problem will usually accept a qualitative description, such as “the curves intersect at the point where they cross on the left side of the region.”
Exam questions will not expect overly fine numerical accuracy when the graph itself does not permit it.
If the crossover is not clearly visible, identify the approximate switching point by observing where the curves appear to touch or approach each other. Then confirm by comparing function values at test x-values on each side.
A graph that is intentionally ambiguous typically signals that the student is meant to rely partially on the algebraic expressions rather than the drawing alone.
Vertical tangents and corners do not change the need to identify the top and bottom functions, but they can make the ordering appear unclear. In such cases:
• Check function values immediately to the left and right of the point.
• Use the algebraic expressions if the graph is visually misleading.
These points do not prevent setting up a valid definite integral as long as the vertical ordering is established.
If the graph seems open, first check whether the problem statement specifies endpoints. Sometimes the axis or another curve acts as an unseen boundary.
If no explicit boundary is stated and the region is genuinely unbounded, you cannot form a finite area integral. AP-style questions will always provide enough information to ensure that the region is properly closed, even if the graph alone does not make this obvious.
Symmetry can reduce the amount of analysis needed if the region is mirrored about the y-axis or a vertical line. It can:
• Indicate that top and bottom functions remain the same on symmetric intervals.
• Allow the use of doubling when the left and right halves of the region match exactly.
However, symmetry only applies when the graph clearly supports it; do not assume symmetry if the drawing or functions do not justify it.
Practice Questions
A region in the plane is bounded by the curves y = 4 − x and y = x, which intersect at x = 2.
(a) Using the graph, state which function is the top function on the interval between the intersection points.
(b) Write, but do not evaluate, the definite integral representing the area of the region between the curves.
Question 1 (1–3 marks)
(a) 1 mark:
Correctly identifies y = 4 − x as the top function on the region between the intersection points.
(b) 2 marks:
1 mark for correct integrand: (4 − x) − x.
1 mark for correct limits: from 0 to 2, or equivalent indication that the intersection points define the interval.
Integral should be written as: ∫ from 0 to 2 of (4 − x − x) dx.
Any equivalent correct form earns full marks.
The curves y = x^2 + 1 and y = 5 − x form a closed region.
(a) Find the intersection points of the two curves.
(b) Determine on which intervals each curve is the top function.
(c) Using your results, set up the definite integral or sum of integrals that represent the total area of the region. Do not evaluate the integrals.
(d) Give one reason, based on the graphs of the curves, why more than one integral may be required.
Question 2 (4–6 marks)
(a) 1 mark:
Correctly solves x^2 + 1 = 5 − x to obtain the intersection points x = −2 and x = 2.
(b) 1 mark:
Identifies that y = 5 − x is the top function on the interval between x = −2 and x = 2.
(c) 2 marks:
1 mark for writing the correct difference of functions: (5 − x) − (x^2 + 1).
1 mark for correct integral setup: ∫ from −2 to 2 of (5 − x − x^2 − 1) dx, or equivalent.
A split into multiple integrals also accepted if correctly justified and written.
(d) 1 mark:
Provides a correct explanation, such as: “If the curves intersect more than once, the top and bottom functions may change, requiring separate integrals for each interval.”

