Area Formula with Right Function Minus Left Function (8.5.2) | AP Calculus AB Notes

AP Syllabus focus:
‘When curves are written as x in terms of y, area is computed with a definite integral ∫_c^d (right function − left function) dy for the region between the curves.’

When regions are described more naturally with vertical boundaries, expressing curves as functions of y allows the area to be computed efficiently using right–minus–left integration.

Understanding Regions Defined by Functions of y

When describing a plane region, it is sometimes more intuitive or more efficient to represent the boundaries as x-values that depend on y. In such cases, curves are rewritten in the form x = g(y) and x = h(y), allowing the region to be understood through horizontal slicing. A horizontal slice has a small thickness dy, and its length corresponds to the horizontal distance between the bounding curves. Since the goal is to accumulate the area of these horizontal slices, the integral naturally runs from y = c to y = d, the vertical bounds of the region.

This graph shows a region bounded by the curves $f(y)=1-y^2$ on the right and $g(y)=y^3-y$ on the left, filled with horizontal strips. Each strip represents a slice of area whose width $W(y)$ equals $\text{right function} - \text{left function}$ . This directly illustrates computing area as $\int_c^d W(y),dy$ when the boundaries are expressed as functions of $y$ . Source.

This perspective is useful whenever expressing the region with respect to x would force multiple integrals or awkward expressions. The AP curriculum stresses choosing this orientation when it simplifies the description of the region and the corresponding definite integral.

The Structure of Horizontal Slices

To compute area using horizontal slices, the student must identify which boundary lies on the right and which lies on the left. The right function gives the larger x-value for a given y, while the left function gives the smaller x-value. The horizontal slice extends from the left boundary curve to the right boundary curve, and its length is the difference between these two x-values.

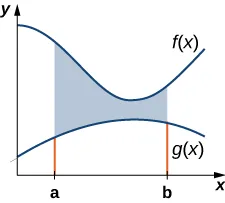
This diagram shows the region between the parabola $x=y^2$ and the line $x=9$ , shaded to emphasize the horizontal extent of each slice. For a fixed value of $y$ , the slice length is $9 - y^2$ , illustrating the “right minus left” structure of the integrand. This makes the area naturally written as an integral with respect to $y$ , $A = \int_c^d (9 - y^2),dy$ , consistent with the syllabus focus on functions of $y$ . Source.

Because area is always accumulated using positive lengths, subtracting left from right ensures a nonnegative expression.

Introducing the distinction between the two curves emphasizes the geometric meaning behind the integral: each thin horizontal slice represents a small rectangular approximation whose width is the horizontal distance between the curves.

The Area Formula for Functions of y

In this context, area is obtained by integrating the horizontal length of the slice with respect to y. This leads directly to the syllabus-required expression of the form right function minus left function over the interval of y-values.

$A(y) = \int_{c}^{d} \big( \text{right function} - \text{left function} \big), dy$
$A$ = Area of the region (square units)
$c, d$ = Lower and upper bounds of y (units consistent with the axes)

This formulation highlights that each slice contributes a small amount of area equal to the slice length multiplied by its differential thickness. It reinforces the principle that definite integrals serve as accumulations of infinitely many small geometric contributions.

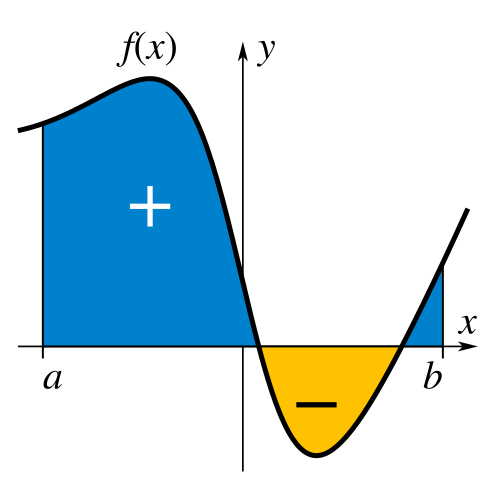
This graph represents a definite integral as the net area between the graph of $f(x)$ and the x-axis from $x=a$ to $x=b$ . The blue region contributes positively while the yellow region contributes negatively, providing context for how definite integrals accumulate signed area. The extra emphasis on signed area extends beyond the syllabus but reinforces understanding of definite integrals before specializing to $\int_c^d (\text{right} - \text{left}),dy$ . Source.

A normal sentence appears here to satisfy placement requirements before introducing additional structural content.

Identifying Right and Left Functions

Correctly determining the right and left boundaries is essential. Students must interpret graphs or equations to determine which function provides the greater x-value for each y in the interval. Key ideas include:

Right boundary: The curve with the higher x-value at a given y.
Left boundary: The curve with the lower x-value at the same y.
Consistency across the interval: The roles of right and left must remain the same from y = c to y = d.
If the curves switch roles, the region must be subdivided so that each integral uses a consistent orientation.

These points reinforce the geometric nature of integration and the importance of graphical reasoning. They also connect to the broader AP theme of determining which variable of integration yields a single, clean definite integral.

Step-by-Step Structure for Setting Up the Integral

To help students build reliable habits, the following list summarizes a clear process for setting up area integrals using functions of y:

Identify the vertical interval of interest by finding intersection points or given y-limits.
Rewrite equations as x = f(y) where necessary.
Determine which curve represents the right function and which represents the left function across the entire interval.
Express the horizontal slice length as right − left.
Write the definite integral with respect to dy using the derived limits.
Confirm that the integrand remains nonnegative on the interval.

Presenting the material in this structured way encourages students to connect conceptual understanding with algebraic execution.

Conceptual Significance for AP Calculus AB

The AP syllabus emphasizes interpreting integrals as accumulation, and the right-minus-left formula exemplifies this perspective. By integrating with respect to y, students see how orientation affects the integrand and how geometry informs the limits and expressions used. This reinforces broader AP goals such as:

Viewing area as accumulated contributions from small geometric slices.
Translating verbal or graphical descriptions into integrals.
Choosing the most efficient variable of integration for a given region.

These ideas align directly with the syllabus requirement that students compute area using the definite integral
$\int_c^d (\text{right function} - \text{left function}), dy$ ,
highlighting how geometry and calculus work together when expressing area using functions of y.

FAQ

A region is better described using functions of y when horizontal slices each touch both boundary curves without interruption.

This usually occurs when the curves can be expressed cleanly as x = f(y), and when vertical slices would require splitting the region or handling changing top and bottom functions.

Choose functions of y if it produces a single, continuous integral with one pair of boundaries.

If the curve that is on the right for some y-values becomes the left curve for others, the interval must be divided into separate sub-intervals.

On each sub-interval:
• Identify which curve is right and which is left.
• Set up a separate integral with consistent orientation.
• Sum the results to obtain the full area.

Horizontal slices ensure that the integrand represents the horizontal distance between the curves.

If this distance is computed incorrectly, such as by subtracting the larger x-value from the smaller, the integrand becomes negative, which does not reflect geometric area.

Using right minus left guarantees that the slice width is always non-negative.

Yes, but only when the geometry forces it.

This happens if neither horizontal nor vertical slices alone can describe the entire region without splitting.

In such cases:
• Divide the region into parts.
• Use x-slicing for one part and y-slicing for another.
• Compute both integrals and add the results.

It can be, especially if one curve already has a simple x = f(y) form.

If the second curve can be expressed in terms of y without excessive algebra, this can simplify the integral.

However, if rewriting the second boundary becomes too complicated, it may be more efficient to reconsider whether using functions of y is the best strategy.

Practice Questions

A region in the plane is bounded on the left by the curve x = y + 1 and on the right by the curve x = 5. The values of y range from y = 0 to y = 3.
Write a definite integral with respect to y that represents the area of this region.
(1–3 marks)

Question 1 (1–3 marks)

• 1 mark: Correct identification of the right-hand function as x = 5 and the left-hand function as x = y + 1.
• 1 mark: Correct integrand written as (5 – (y + 1)) or equivalent.
• 1 mark: Correct limits of integration, 0 to 3, and correctly written definite integral.

A fully correct answer:
∫ from 0 to 3 of (5 – (y + 1)) dy
(3 marks)

1. The region R is bounded on the left by the curve x = y^2, on the right by the curve x = 8, and vertically between y = –2 and y = 2.
(a) Sketch or describe the shape of the region R, identifying clearly which boundary is the right-hand curve and which is the left-hand curve.
(b) Set up, but do not evaluate, the definite integral with respect to y that represents the area of R.
(c) Explain why integrating with respect to x would be less efficient in this case.
(4–6 marks)

Question 2 (4–6 marks)

(a)
• 1 mark: Identifies x = y^2 as the left boundary (smaller x-values).
• 1 mark: Identifies x = 8 as the right boundary.
• 1 mark: Correct description that the region extends vertically from y = –2 to y = 2.

(b)
• 1 mark: Correct integrand (8 – y^2) or equivalent.
• 1 mark: Correct definite integral written from y = –2 to y = 2.

(c)
• 1 mark: States clearly that integrating with respect to x would require splitting the region or inverting the parabola, making the integral more complicated.

A fully correct answer:
Area = ∫ from –2 to 2 of (8 – y^2) dy
(6 marks)

Try All Topic Practice Questions

Written by:

Dr Rahil Sachak-Patwa

Oxford University - PhD Mathematics

Rahil spent ten years working as private tutor, teaching students for GCSEs, A-Levels, and university admissions. During his PhD he published papers on modelling infectious disease epidemics and was a tutor to undergraduate and masters students for mathematics courses.