AP Syllabus focus:
‘Students decide whether to integrate with respect to x or y, selecting the orientation that gives a single definite integral or simpler description of the region.’
Choosing the correct variable of integration allows areas between curves to be expressed with the simplest possible definite integral, ensuring clearer region descriptions and more efficient setup.
Understanding the Choice of Integration Variable
When finding the area between curves in the plane, students must decide whether integrating with respect to x or with respect to y gives the most direct and manageable representation of the region. This decision follows from recognizing how the region is bounded and which orientation yields a single integral instead of multiple integrals.
Because area can be described using horizontal or vertical slices, the variable of integration determines the direction in which the region is sliced.
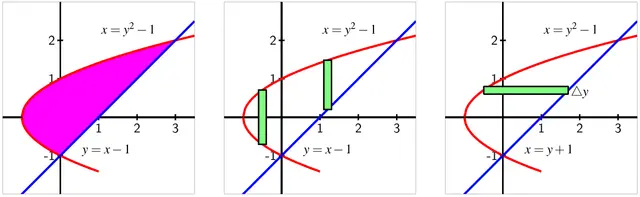
This three-panel diagram shows a region between two curves, then approximates its area using vertical slices in the middle panel and a horizontal slice in the right panel. It visually contrasts integrating with respect to x versus integrating with respect to y. The curves and numerical labels extend beyond syllabus requirements but simply illustrate one concrete example. Source.
Vertical Slice: A rectangular element whose height is determined by functions of x and whose width is an infinitesimal change in x.
A normal sentence ensures smooth continuation. Vertical slices are most natural when curves are given as y-values that are easy to compare on an interval of x-values.
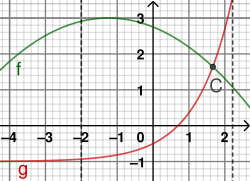
This diagram plots two functions with a shaded region representing the area between them using vertical slicing. It visually reinforces the “top minus bottom” interpretation used when integrating with respect to x. The specific forms of the curves are illustrative and not required by the syllabus. Source.
Area Formulas and Orientation
Once a slicing direction is selected, the appropriate definite integral formula follows automatically. Integrating with respect to x typically measures vertical distance between two functions, while integrating with respect to y measures horizontal distance.
= Area of the region (square units)
= Independent variable describing vertical slices (units depend on context)
A normal sentence separates equation blocks. In many regions, however, horizontal slicing produces a more concise description.

This figure shows a region between two curves shaded with horizontal bands, emphasizing that horizontal slices naturally describe this region. It demonstrates why integrating with respect to y sometimes avoids splitting the region into multiple integrals. The specific functions provide extra context beyond syllabus requirements but illustrate the principle clearly. Source.
= Independent variable describing horizontal slices
= Functions defining horizontal boundaries
Criteria for Choosing x or y Integration
Structural Considerations
Students determine which orientation simplifies the integral by analyzing the region’s boundaries in detail.
Key considerations include:
How the region is bounded. Determine whether boundaries are easier to express in terms of x or y.
Whether one orientation avoids splitting the region. A single slice direction that spans the entire region without interruption is preferred.
Which orientation aligns with the simplest functional relationships. If curves are explicitly written as y in terms of x, vertical slicing is often favored.
Whether inversion is necessary. Sometimes re-expressing a function as x in terms of y allows a more efficient setup.
Situations Favoring Integration with Respect to x
Students should integrate with respect to x when:
The top and bottom boundaries can be described as functions of x over a closed interval.
Vertical slices intersect the region exactly once across the entire domain.
Functions are naturally given in the form y = f(x), avoiding algebraic rearrangement.
Situations Favoring Integration with Respect to y
Integration with respect to y is advantageous when:
The region’s boundaries are more naturally viewed as right and left functions of y.
Vertical slices would require breaking the region into subregions due to changing top and bottom curves.
The problem statement explicitly rewrites functions as x = g(y) or provides tabular data in terms of y.
Visual Analysis for Selecting Orientation
Graphical Interpretation
A clear sketch often reveals which integration direction yields a simpler description. Students inspect:
Where slices intersect bounding curves.
Whether vertical slices change which function is on top.
Whether horizontal slices change which function is on the right.
If vertical slices encounter a switch in top/bottom functions but horizontal slices remain consistent, integrating with respect to y leads to a single integral and cleaner setup.
Intersection-Based Decisions
To maintain a single definite integral:
Identify points where curves intersect.
Determine if these intersections segment the region when slicing vertically or horizontally.
Choose the orientation that avoids piecewise definitions.
Procedural Steps for Selecting x or y Integration
Students can follow a structured approach:
Sketch the region to visualize boundaries.
Identify functional forms: decide which variable each boundary is expressed in.
Examine slice behavior: check for switches in top/bottom or left/right functions.
Choose the simpler orientation that produces a single integrand and avoids splitting regions.
Confirm bounds based on the chosen variable, using intersection points or endpoints as needed.
Role of the Syllabus Requirement
The AP Calculus AB syllabus emphasizes that students must “select the orientation that gives a single definite integral or simpler description of the region.” This means the choice must always be justified by clarity and simplicity, not by arbitrary preference. By learning to compare vertical and horizontal slicing, students develop flexibility in setting up area integrals that align with the structure of the region being analyzed.
Selecting the appropriate variable of integration strengthens conceptual understanding and ensures efficient problem-solving when finding areas between curves.
FAQ
Look for any point where the curve that appears to be on top crosses below another curve when viewed vertically. If the relative vertical ordering changes even once, vertical slices cannot describe the whole region in a single integral.
A fast check is to trace a pencil straight down the page: if it hits the same two curves in the same order throughout, vertical slicing works cleanly.
Choose the orientation that keeps the integrand simpler to write. Even when both give single integrals, one may produce a polynomial while the other produces a reciprocal or root.
You may also prefer the orientation whose bounds are easier to determine, especially if one set of bounds requires solving a messy intersection equation.
Graphical shape matters as much as algebraic complexity. Even if two functions are easy to compute with, the region between them may bend or loop in a way that breaks a slice’s path.
If any slice intersects the region in two disconnected pieces, that orientation must be split into multiple integrals.
Yes. Rearranging may produce multiple branches, such as when taking square roots. If the curve splits into two x-values for the same y-value, horizontal slicing becomes impractical or impossible.
Before committing to integrating with respect to y, check whether the rewritten expression gives a one-to-one horizontal boundary.
Yes. If one orientation forces an integrand that changes sign, you would need absolute values or piecewise expressions to correct it.
Choosing the orientation where the bounding function differences stay positive simplifies the integral and reduces the risk of sign errors.
Practice Questions
(1–3 marks)
A region in the plane is bounded above by the curve y = 4 − x and below by the curve y = x − 2.
Explain whether integrating with respect to x or with respect to y allows the area of this region to be found using a single integral.
(1–3 marks)
• 1 mark for identifying the correct orientation: integrating with respect to x.
• 1 mark for explaining that the top and bottom curves are already expressed as functions of x and do not switch order over their intersection interval.
• 1 mark for correctly noting that integrating with respect to y would require rearranging both functions into x expressed in terms of y.
(4–6 marks)
A region R is bounded by the curves y = x², y = 2x + 3, and x = −1.
(a) Determine whether vertical or horizontal slices will allow the area of R to be expressed as a single definite integral.
(b) Set up, but do not evaluate, the definite integral for the area of R using your chosen orientation.
(c) Justify why the alternative orientation would require splitting the region.
1.(4–6 marks)
(a)
• 1 mark for choosing vertical slices (integration with respect to x).
• 1 mark for stating that vertical slices intersect the region without the top and bottom curves switching roles.
(b)
• 1 mark for giving correct limits of integration: from x = −1 to the x-value where x² and 2x + 3 intersect.
• 1 mark for correctly setting up the integral of (upper function minus lower function): area = integral from x = −1 to intersection of (2x + 3 − x²) dx.
(c)
• 1 mark for clearly stating why horizontal slices fail: the right-hand boundary alternates between x = −1 and the rearranged form of y = 2x + 3, causing the region to be split.

