A region in the plane can often be analyzed more efficiently by expressing its boundaries as functions of y, especially when vertical description simplifies geometry and integral setup.

Describing Regions Using Functions of y

Representing regions using functions of y involves rewriting boundary curves in the form $x = g(y)$ or $x = h(y)$ so that the region is described over a vertical interval. This method is particularly helpful when horizontal slices offer a clearer or single-integral representation of area. The goal is to structure the region so that every horizontal slice spans from a left boundary to a right boundary, allowing a straightforward definite integral with respect to $y$.

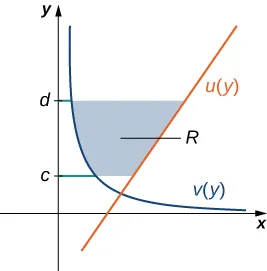
This diagram shows a region $R$ bounded on the left by the curve $x = v(y)$ and on the right by $x = u(y)$, for $y$ between $c$ and $d$. It illustrates how a region can be fully described by specifying a vertical interval $[c,d]$ together with left and right boundary functions of $y$. This supports the idea that each horizontal slice of the region has a clearly defined start and end in the $x$-direction. Source.

When Describing a Region with Respect to y is Advantageous

In many problems, vertical slices (integration with respect to $x$) may require multiple integrals or produce unnecessarily complicated expressions. By rotating perspective, students often obtain:

• A simpler domain defined by $c \le y \le d$

• A clear pairing of left and right boundary curves

• A single expression for area rather than piecewise descriptions

• A more direct representation of geometric or physical constraints expressed naturally in terms of $y$

This perspective aligns with the specification’s emphasis on choosing the functional orientation that most efficiently represents the region.

Boundary Curves Rewritten as Functions of y

A boundary originally given as $y = f(x)$ can frequently be solved for $x$, producing a relation of the form $x = f^{-1}(y)$, provided the inverse exists on the interval of interest. Once rewritten, the expression assigns a unique horizontal position to each height $y$ in the region. This becomes the foundation for integral expressions used later in area calculations, although the area formulas themselves belong to other subsubtopics.

Rewriting boundaries in terms of $y$ also clarifies how the region extends vertically. Many regions have natural top and bottom limits that appear explicitly once the functions are expressed as $x$ in terms of $y$.

Vertical Extent of the Region

The interval $[c,d]$ represents all $y$-values for which the region exists. Identifying this interval requires determining where boundary curves begin and end vertically. This step is essential because horizontal slices must fully lie within the region for all $y$ between $c$ and d.

Students are expected to read graphs and determine this interval by:

• Locating intersection points of the boundary curves

• Observing the lowest and highest $y$ values included in the region

• Ensuring that each horizontal slice is bounded by consistent left–right curves

A clear vertical interval ensures that the region is represented smoothly and without gaps.

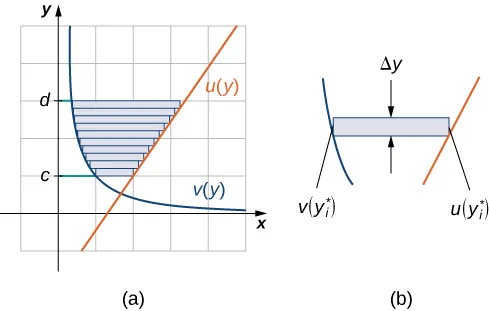
This diagram depicts the region between $x = v(y)$ and $x = u(y)$ subdivided into horizontal rectangles of thickness $\Delta y$. Each rectangle spans from the left boundary curve to the right boundary curve at a fixed $y$-value, visually encoding the width $u(y) - v(y)$ of a horizontal slice. The presence of $\Delta y$ anticipates later area computations while emphasizing how the region is structured using functions of $y$. Source.

Left and Right Boundaries of the Region

Once the vertical interval is known, each horizontal slice spans from a left boundary curve to a right boundary curve. These boundaries must be expressed explicitly as functions of y.

A sentence is included here to separate definition blocks appropriately.

Understanding which curve lies on each side is crucial. Graphs often help determine relative placement, especially when curves change orientation or when the algebraic form alone does not clearly indicate left–right relationships.

This graph shows a shaded region bounded between the curves $x = f(y) = 1 - y^2$ and $x = g(y) = y^3 - y$, with $y$ ranging approximately from $-1$ to $1$. It demonstrates how left and right boundary curves of a region can be represented naturally as functions of $y$, clarifying which curve forms each boundary at any given height. The hatched shading emphasizes the region without introducing concepts beyond those needed to describe boundaries in terms of $y$. Source.

Interpreting Regions Described with Functions of y

Describing regions with respect to $y$ provides a geometric translation that supports deeper conceptual understanding. Students learn to see:

• Horizontal slices as representations of width

• Vertical intervals as indicators of the region’s full height

• Left/right boundaries as constraints determining the slice’s horizontal extent

These observations reinforce the idea that a region’s area is built from the accumulation of widths stacked vertically, even though the explicit integral expression belongs to the subsequent subsubtopic.

Conceptual Importance for Later Integration

Although area computation is covered elsewhere, the conceptual groundwork begins here. AP Calculus AB emphasizes understanding accumulation in geometric contexts, and describing regions using functions of y offers an alternative orientation for such accumulation. Students gain flexibility in analyzing regions and choosing an appropriate approach depending on the geometry of the problem.

The specification highlights this flexibility: some regions simply cannot be described efficiently using functions of x, but rewrite naturally in terms of $y$. Developing fluency with both orientations allows students to set up integrals correctly, generate accurate representations of regions, and interpret graphs with confidence.

Process for Describing a Region Using Functions of y

Students typically follow a structured approach:

• Identify the curves that bound the region.

• Rewrite each boundary in the form $x = g(y)$ or $x = h(y)$, when possible.

• Determine the vertical interval $[c,d]$ by locating the minimum and maximum $y$ values present in the region.

• Establish which curve acts as the left boundary and which acts as the right boundary over this entire interval.

• Confirm that every horizontal slice intersects the region exactly once on each side to avoid piecewise descriptions.

Mastering this method equips students with tools needed for more advanced area and volume problems that depend on describing regions accurately before integrating.