This subsubtopic explains how using an absolute value inside a definite integral guarantees a nonnegative measure of vertical distance between curves, even when the top and bottom functions switch.

Using the Integral of the Absolute Value of a Difference

When determining the area between two curves, students often subtract the lower function from the upper function on a given interval. However, when the relative positions of the curves change, identifying which function is greater at each subinterval can become inefficient or unclear. The integral of the absolute value of the difference provides a consistent method to ensure that accumulated area remains nonnegative regardless of which curve lies above the other.

Understanding Vertical Distance

The vertical distance between curves at a point $x$ refers to the magnitude of the difference in their $y$-values. Since area must always be nonnegative, the integrand should never be allowed to take on negative values. The absolute value resolves this issue by ensuring positivity. Whenever the value of $f(x) - g(x)$ changes sign, the integral of $|f(x) - g(x)|$ continues to accumulate distance without requiring manual subdivision of the interval.

Between graphs that may cross multiple times, this definition guarantees that the expression inside the area integral represents the actual separation rather than a signed quantity. This allows the absolute-value integral to function as a general tool for constructing area expressions without the need for piecewise analysis unless simplification is desired.

The Absolute Value Integral as Total Enclosed Area

Using the integral of the absolute value of a difference gives a single expression for the area between curves on an interval $[a, b]$:

This formulation corresponds directly to the syllabus requirement: the integrand must represent a nonnegative quantity. Because the absolute value automatically adjusts to whichever function lies above at a point, the approach is particularly useful if intersections are difficult to solve analytically or if the region switches configuration often.

A key feature of this method is that it mirrors how area is treated geometrically: area accumulates magnitude only, without regard to orientation. Without the absolute value, a definite integral of $f(x) - g(x)$ could produce cancellation, distorting the actual enclosed area. The absolute value prevents such cancellation.

When the Absolute Value is Especially Useful

Students encounter situations in which the absolute value integral provides a cleaner or more reliable representation of area. Common conditions include:

• Multiple intersection points where determining subintervals manually would be cumbersome.

• Alternating top and bottom curves, making the usual “top minus bottom” formula unstable across $[a,b]$.

• Graphs defined by tables or data where the ordering of $f$ and $g$ is not algebraically obvious.

• Contextual problems where sign changes occur unpredictably and precise decomposition is unnecessary for conceptual understanding.

Each of these circumstances benefits from a method that ensures correct accumulation of area even when algebraic complexity increases. The absolute value thus streamlines the process while preserving mathematical correctness.

Conceptual Meaning of the Absolute Value

The presence of the absolute value indicates that the integral is accumulating a distance rather than a net difference. Whereas $\int (f(x) - g(x)),dx$ measures signed area, the expression with $|f(x) - g(x)|$ captures the full geometric region. This interpretation aligns closely with the idea of area as a physical quantity, reinforcing the foundational principle that area is inherently nonnegative.

A definite integral of a real-valued function represents a signed area, where regions below the x-axis contribute negative area.

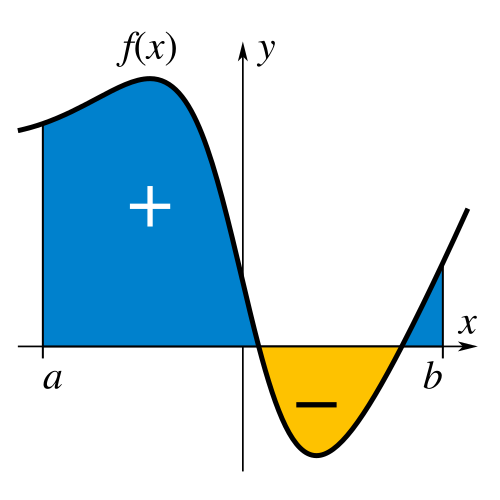
This graph shows a function with regions above and below the x-axis shaded in distinct colors, illustrating positive and negative signed areas. It highlights that $\int_a^b f(x),dx$ can include both positive and negative contributions. The geometric region may appear similar, but the sign difference affects the integral’s value. Source.

Between any two definition blocks, regular sentences are present to maintain clarity. Understanding the distinction between signed area and geometric area helps students appreciate why the absolute value formulation is necessary in certain integral applications.

Structure of the Integrand

The integrand $|f(x) - g(x)|$ embodies the magnitude of separation between curves. Because the absolute value function measures distance on the real number line, it naturally fits the requirement for representing the vertical separation of curves. Additional insights into the behavior of the integrand include:

• When f(x) > g(x), the integrand simplifies to $f(x) - g(x)$.

• When f(x) < g(x), it becomes $g(x) - f(x)$.

• At intersection points where $f(x) = g(x)$, the integrand is zero, but this does not affect total area.

We can interpret $\int_a^b |f(x)-g(x)|,dx$ as the accumulated area of infinitely many thin vertical strips between the two graphs over $[a,b]$.

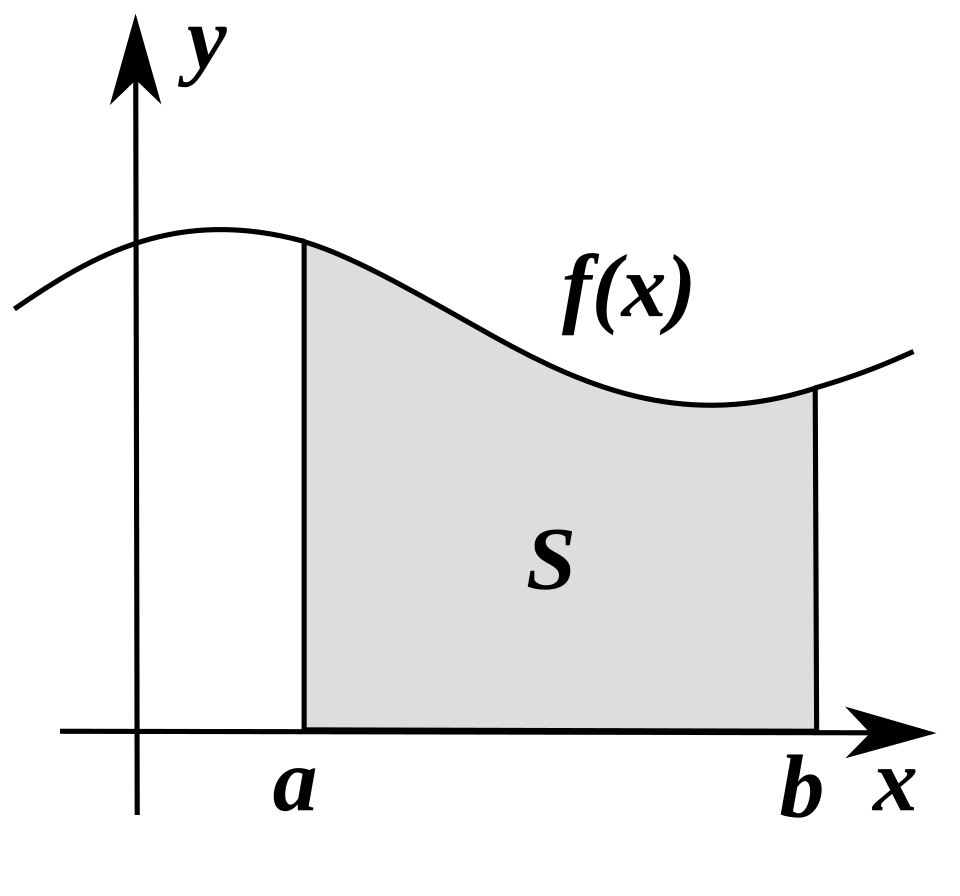
This diagram shows $y=f(x)$ with the region under the curve shaded from $x=a$ to $x=b$. It illustrates the definite integral as accumulated area formed by thin vertical slices. Though shown for a single curve, the same idea applies when slice height equals $|f(x)-g(x)|$. Source.

Notably, the integral does not require explicit partitioning where the curves cross, though doing so may sometimes simplify evaluation.

Interpreting the Absolute Value Graphically

Graphically, the quantity $|f(x) - g(x)|$ corresponds to the vertical distance between the two curves at each value of $x$. This perspective reinforces the geometric meaning of the area integral. Regardless of orientation, the distance remains measured as a nonnegative quantity, maintaining consistency with the procedure required for computing enclosed area.

Benefits for Applied or Complex Regions

In applied contexts or when working with irregularly shaped regions, the absolute value approach provides an efficient and reliable method. Because it avoids assumptions about which function lies above, it aligns naturally with situations where modelled phenomena cross or fluctuate. Whenever $f$ and $g$ intersect, the identity of the top and bottom curves changes, so we split the interval at those intersection $x$-values and evaluate separate integrals on each subinterval.

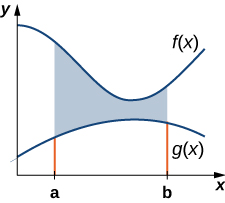
This graph displays $y=\sin x$ and $y=\cos x$ with the region between them split into two subregions. One curve lies above the other in each subregion, illustrating how the vertical distance $|f(x)-g(x)|$ changes at intersection points. The extra labels (R1 and R2) help highlight the shift in which function is on top. Source.