AP Syllabus focus:
‘Students interpret graphs where the top and bottom curves change, setting up sums of definite integrals or absolute-value integrals to represent the total enclosed area.’
Applied area problems with shifting upper and lower boundaries require careful interpretation of graphs so integrals correctly represent accumulated area, even when curve dominance changes across intervals.
Understanding Changing Top and Bottom Curves
When a region’s top function and bottom function change roles across different portions of the domain, students must reinterpret the geometry at each subinterval. These situations arise when curves intersect multiple times or when contextual conditions cause one quantity to exceed another only on certain intervals. The central idea is to view area as accumulated vertical distance between functions, adjusting integrals so the integrand remains nonnegative across all pieces of the region.
Intersection Points and Shifting Dominance
Intersection points determine where dominance switches. Because area must represent the positive vertical separation, the student must confirm which curve lies higher between each pair of consecutive intersection values. This ensures that integrals reflect the correct structure of the region, avoiding sign errors that would artificially reduce area. In modeling contexts, dominance may correspond to which rate, cost, or physical quantity exceeds another, meaning such analysis is both geometric and conceptual.
Key Terminology in Applied Area Problems
When exploring regions with variable dominance, the ideas of enclosed region, vertical separation, and piecewise accumulation become essential. Each term reinforces how definite integrals model physical or contextual quantities.
Enclosed Region: The set of all points between two curves on an interval where the curves form boundaries of a finite area.
Between changes in curve dominance, the integrand must reflect the correct relationship between the functions. This prevents any misinterpretation of the region, especially when dealing with irregular or real-world shapes.
Constructing Appropriate Integrals for Applied Settings
Applied problems often provide graphs or descriptions instead of explicit formulas. Students must translate these representations into integrals that reflect how the region behaves. When dominance is constant, one integral suffices. When dominance changes, multiple integrals are needed, each tailored to its subinterval. Alternatively, a single integral incorporating an absolute value may be used when the problem structure allows it.
Using Standard Area Integrals
The typical area representation uses the difference between the top and bottom functions on each subinterval. Because area must be nonnegative, integrals must be separated where necessary to preserve positivity.
On any interval where one curve is always above the other, the geometric area is ∫(top − bottom) dx over that interval.
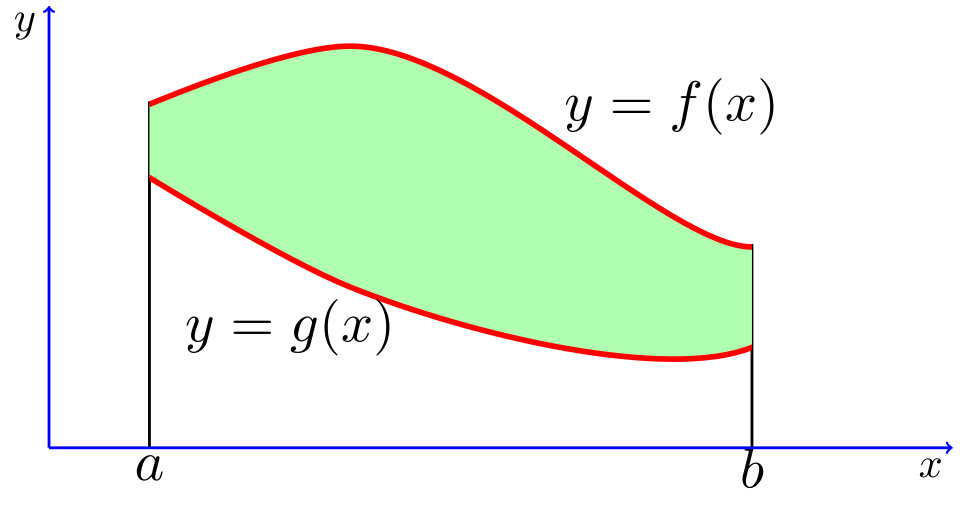
This graph shows two functions, labeled and , with the region between them shaded between and . It illustrates how geometric area corresponds to the vertical distance “top minus bottom” accumulated along the interval. This supports the formula for a region where the same function stays on top. Source.
= Area between the two curves on the interval
= Vertical distance between functions
This form aligns with geometric intuition: a small rectangular slice has height equal to the vertical separation of the curves, and the integral sums infinitely many such slices.
Because definite integrals compute signed area, regions where the vertical difference is negative would otherwise subtract from the total.
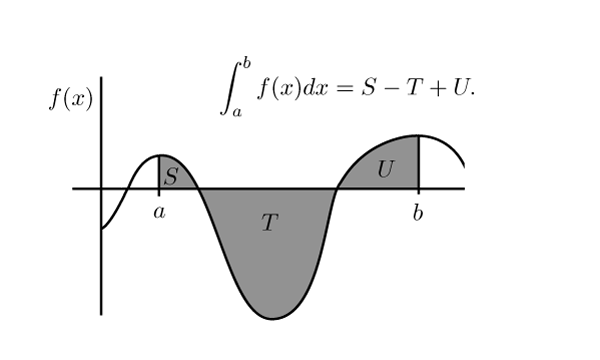
This figure shows a curve crossing the -axis, with areas above the axis shaded and labeled positive and areas below shaded and labeled negative. It highlights that a standard definite integral returns the net signed area rather than total geometric area. In applied top–bottom problems, this motivates using or splitting intervals to keep the integrand nonnegative. Source.
A single equation cannot always describe the region when the ordering of curves changes. Instead, structure is imposed by partitioning the domain and creating a sum of integrals, each capturing only the portion where a single dominance condition holds.
Applying Absolute Value to Area Integrals
When applied contexts favor a single expression or when the functions cross multiple times but are difficult to analyze piecewise, the integral of the absolute value is useful. The absolute value ensures a nonnegative integrand regardless of which function is larger.
= Total area enclosed by the two curves on the interval
= Magnitude of the vertical separation
This representation captures the total area without requiring explicit piecewise structure, though students must still conceptually understand where and why dominance changes. Applied problems often provide graphs indicating varying performance, flow, or measurements that cross over time; the absolute-value formulation preserves the full magnitude of these differences.
Process for Setting Up Area Integrals in Context
Students benefit from a clear procedure to structure applied area problems where curve roles change. The following steps outline the necessary reasoning:
Identify the interval on which the region exists, using context or graphical information.
Locate intersection points of the curves, either visually or by interpreting the provided functions or data.
Determine which function is on top on each subinterval formed by the intersection points.
Express area integrals piecewise using the top-minus-bottom structure or construct a single absolute-value integral if the problem calls for it.
Interpret the meaning of each integral in context, recognizing what the vertical distance represents (e.g., difference in rates, costs, outputs, or physical measurements).
Understanding each step supports accurate modeling and ensures that area is interpreted correctly in applied scenarios.
Interpreting Applied Graphs with Changing Dominance
In many applications, graphs represent data such as supply and demand, pollutant concentration, or velocity profiles. The area between these graphs may model net differences in quantity, energy, cost, or displacement. When curve dominance flips, these changes reflect real transitions — moments when one quantity overtakes another in significance. Recognizing these transitions reinforces the broader AP Calculus AB theme that definite integrals represent accumulated change, whether geometric or contextual.
In an applied setting, the region whose area we want is always some vertical strip or collection of strips between two graphs over a stated interval of x.
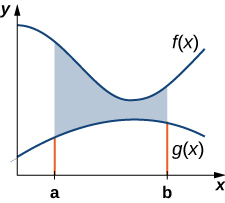
This figure shows two functions, labeled and , with the region between them shaded from to . It emphasizes that the area in question is the collection of all vertical slices between the graphs over the specified interval. Some surrounding text mentions Riemann rectangles, which provide additional context but exceed the specific requirements of the AP syllabus. Source.
FAQ
Look first for the intersection points, as they are the only locations where the ordering of the curves can change.
Then inspect each subinterval between intersection points and compare the vertical positions of the curves by checking a single sample point in each region. This avoids scanning the entire graph and reduces visual overload.
If the graph is dense, trace each curve lightly with your finger or a straightedge to track which one lies higher.
No. If the problem provides a clearly labelled graph, you may use the intersection points shown on the diagram, even if they are not numerically specified.
However, when the problem relies on precise calculations or asks for an exact expression, you must determine the intersection points algebraically.
If estimation is acceptable, the exam question will explicitly indicate that graphical or numerical reasoning is allowed.
Students often integrate the entire interval using a single difference, forgetting to account for where the roles change.
This leads to cancellation of positive and negative areas, giving an answer far smaller than the true geometric area.
Avoid this by listing all subintervals before writing any integrals and checking that the integrand remains positive on each.
Contextual descriptions often imply dominance even before looking at a graph:
• If a rate, cost, or measurement is described as larger or exceeding another over a period, that function is likely the top function for that interval.
• If the problem mentions crossover points or switching conditions, these usually correspond to intersection points.
Use these clues to confirm or guide your interpretation of the graph.
It is preferable when:
• The curves intersect many times and writing piecewise integrals would be lengthy.
• The problem emphasises total magnitude rather than the details of each interval.
• The expression is purely symbolic and the examiner expects a compact form.
However, when a question asks explicitly about which function is on top, you should still use piecewise integrals.
Practice Questions
A region in the plane is bounded by two functions f and g over the interval 0 ≤ x ≤ 4. The graphs of f and g intersect at x = 1 and x = 3.
(a) State how the total area between the curves should be computed when the top and bottom functions change between intervals.
(a)
• 1 mark for stating that the area must be split into separate integrals on intervals where one function is consistently on top.
• 1 mark for stating that each integral should use top minus bottom.
(max 2 marks)
A pollutant concentration in a lake is modelled by two functions, C1 and C2, measured in milligrams per litre, over the time interval 0 ≤ t ≤ 10 hours.
The graphs of C1 and C2 intersect at t = 2 and t = 7.
• On 0 ≤ t < 2, C1 lies above C2.
• On 2 ≤ t < 7, C2 lies above C1.
• On 7 ≤ t ≤ 10, C1 again lies above C2.
(a) Write an expression for the total area between C1 and C2 over 0 ≤ t ≤ 10.
(b) Explain the meaning of this area in the context of the problem.
(c) State how the integral expression would change if the examiner required a single integral involving the absolute value of the difference of the functions.
(a)
• 1 mark for correctly identifying the three subintervals: 0 to 2, 2 to 7, and 7 to 10.
• 1 mark for writing the area on 0 to 2 as the integral of (C1 − C2).
• 1 mark for writing the area on 2 to 7 as the integral of (C2 − C1).
• 1 mark for writing the area on 7 to 10 as the integral of (C1 − C2).
(max 4 marks)
(b)
• 1 mark for stating that the area represents the total difference in pollutant concentration between the two measurements over time.
• 1 mark for noting that it measures accumulated magnitude of separation, not signed difference.
(max 2 marks)
(c)
• 1 mark for stating that a single integral of the absolute difference, integral of |C1 − C2| from 0 to 10, would be used.
(max 1 mark)

