AP Syllabus focus:
‘When curves intersect multiple times, the region between them may be split into subregions, each described by its own definite integral for area on a subinterval.’
When two curves intersect at more than two points, students must separate the overall region into smaller, manageable subregions to compute area correctly using appropriate definite integrals.
Understanding Regions Formed by Multiple Intersections
When two functions intersect repeatedly over an interval, the region enclosed between them may change shape, orientation, or which function lies above the other. This subsubtopic focuses on how to correctly split such regions into subregions and assign a definite integral to each portion. Because the standard method for area between curves relies on identifying a consistent top function and bottom function, multiple intersections require additional organizational steps to apply integration properly.
The Need for Subdivision
When curves intersect more than twice, the spatial relationship between them typically shifts along the domain. In some portions of the interval, one function may lie above the other, while in adjacent portions the roles reverse. This shifting makes it impossible to write a single definite integral that uses one consistent difference of functions. Instead, students must divide the region into separate intervals, each having:
A clear and unchanging top and bottom function over that subinterval
A definite integral representing area between the curves
Clearly identified intersection points that serve as boundaries
These divisions ensure that each integral computes an area that is always nonnegative without requiring absolute values in the integrand.
A graph of the curves forming two shaded subregions R1R_1R1 and R2R_2R2, illustrating that each lies on an interval with a consistent top and bottom function. The figure demonstrates how splitting the region ensures each integral correctly represents nonnegative area. The visual emphasizes that total area equals the sum of the areas of the subregions. Source.
Identifying Intersection Points
The starting point for handling regions with multiple intersections is determining all intersection points within the relevant domain. Intersection points occur where the two curves share the same output value.
Intersection Point: A value of for which two functions satisfy , representing a shared point on their graphs.
To compute or estimate these points, students may use algebraic solving, graphical intersection features, table values, or other given information. These points become the boundaries dividing the overall region into smaller segments where the graph configuration remains consistent.
After identifying all intersection points, students analyze each interval between consecutive intersection points to determine which function is above the other. This step is essential because the vertical ordering determines the integrand used to compute the region’s area.
Ensuring Correct Integrand Construction
To compute area between curves on a subinterval, the formula requires that the integrand represent the vertical distance between functions. Because this distance must always be nonnegative when representing area, the functions must be ordered properly on each interval. That distance is the difference between the top and bottom functions.
= The subinterval boundaries determined by intersection points
Between every pair of intersection points, the ordering of curves stays consistent. Students verify this ordering by evaluating the functions at a sample point or by examining their graphs. Only after this analysis can a correct definite integral be assigned to the subregion.
Students must note that a single overall region might consist of two, three, or more such subregions, depending on how many times the curves intersect.
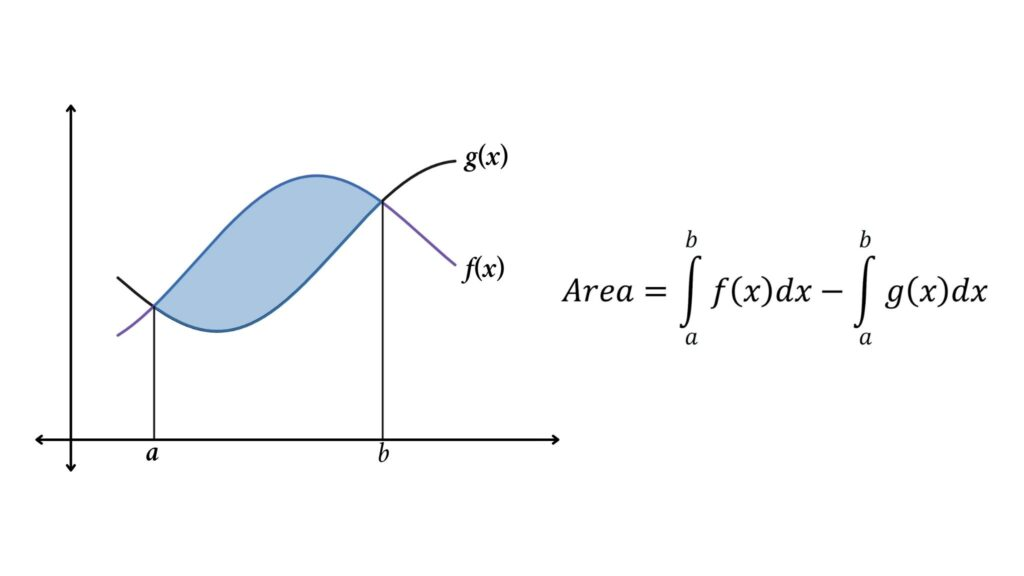
A pair of intersecting curves with the shaded region split at the intersection point ccc into two intervals. The total area is shown as the sum of two integrals, demonstrating why the integrand must change when the top and bottom curves swap. The surrounding article adds broader context beyond the AP subsubtopic but remains visually useful. Source.
Organizing the Process of Splitting Regions
A structured method helps prevent common errors and ensures that each subregion is correctly represented. Students benefit from following a logical sequence whenever multiple intersections occur.
A Process-Oriented Framework
Identify all intersection points of the two curves within the relevant interval.
Sort these intersection points in ascending numerical order to create distinct subintervals.
Examine each subinterval to determine which function lies above and which lies below.
Construct a definite integral for each subinterval using the difference of the two functions.
Express the total enclosed area as a sum of the integrals over the subintervals.
Evaluate or estimate each definite integral separately when required.
This systematic approach ensures clarity and prevents mixing intervals where the functions change orientation.
When Subregions Become Necessary
Multiple-intersection cases arise in various contexts, especially when curves cross back and forth or when one curve oscillates relative to another. In such scenarios, the total area cannot be captured by a single integral. Splitting the region reflects the reality that the geometric structure of the region changes, even if subtly, across different portions of the domain.
Visual and Conceptual Benefits of Subdivision
Subdivision clarifies how the region’s shape evolves along the -axis.
Students see that each subregion contributes independently to the total area.
The method reinforces the idea that area accumulation is additive, allowing integration to reflect the geometry accurately.
It emphasizes the principle that definite integrals accumulate signed quantities, but area must remain nonnegative within each portion of the region.
By isolating segments where the functions’ ordering stays constant, students apply the area formula cleanly and avoid incorrect negative contributions.
Connecting Subregions to the Larger Concept of Area Between Curves
Splitting regions with multiple intersections highlights the broader AP Calculus AB principle that definite integrals represent accumulated quantities over intervals where the integrand maintains consistent meaning. Just as students break complex motion or accumulation problems into manageable intervals, they also break geometric regions into subregions when necessary. This reinforces the conceptual understanding that area calculations must reflect the true structure of the region, respecting where curves meet, change position, or redefine the boundaries of the enclosed space.
FAQ
A useful approach is to analyse the general behaviour of the curves. If one function oscillates, is non-monotonic, or visibly crosses the other more than once on a graph, splitting will likely be required.
You can also check sign changes in the difference f(x) – g(x); if this expression changes sign within the interval, the curves must switch order, indicating the need for subregions.
Yes. For area set-up questions, the AP exam allows you to use visually estimated intersection points when exact values are not required by the problem.
However, if the problem later requires numerical evaluation, you must use the values provided in the question or compute them using algebra or technology if permitted.
Use a structured check:
• Evaluate both functions at a convenient test point within each suspected subinterval.
• Compare their values numerically to determine which is larger.
• If necessary, zoom in on the graph or examine a table of values.
This prevents misidentifying the top function, which would produce incorrect integrands.
Yes. If the curves come close but do not intersect, they form a single continuous region with a consistent ordering.
A split is only required when an actual crossing occurs, altering which curve lies above the other.
It can. If you integrate with respect to y, you must identify where the curves intersect vertically, which may differ from the horizontal intersection structure.
When the region is complex, choose the orientation that minimises the number of subregions. This often simplifies both the analysis and the required integral expressions.
Practice Questions
Question 1 (1–3 marks)
The graphs of two functions f and g intersect at x = 1 and x = 4. On the interval 1 ≤ x ≤ 4, the functions cross again at x = 2, after which g lies above f.
(a) Write an expression for the total area between the curves on the interval 1 ≤ x ≤ 4 by splitting it into appropriate subregions.
Question 1
(a)
• 1 mark: Identifies the need for two integrals based on the second intersection at x = 2.
• 1 mark: Correctly sets up the area from 1 to 2 using the correct top and bottom functions (f above g).
• 1 mark: Correctly sets up the area from 2 to 4 using the correct top and bottom functions (g above f).
Total: 3 marks.
A correct answer is of the form:
Area = ∫ from 1 to 2 of (f(x) – g(x)) dx + ∫ from 2 to 4 of (g(x) – f(x)) dx.
Question 2 (4–6 marks)
The curves y = h(x) and y = k(x) intersect at x = -3, x = 0, and x = 5. On the interval -3 < x < 0, h(x) is above k(x). On the interval 0 < x < 5, k(x) is above h(x).
(a) Explain why the region between the curves must be split into two subregions when finding its area.
(b) Write a sum of definite integrals that represents the total area of the region between the curves.
(c) State one reason why writing a single integral from -3 to 5 using h(x) minus k(x) would be incorrect.
Question 2
(a)
• 1 mark: States that the curves swap which one is on top at x = 0.
• 1 mark: Explains that this change requires separate integrals to keep the integrand non-negative.
(b)
• 1 mark: Correct integral set-up on -3 to 0 with h(x) above k(x).
• 1 mark: Correct integral set-up on 0 to 5 with k(x) above h(x).
A correct answer is of the form:
Area = ∫ from -3 to 0 of (h(x) – k(x)) dx + ∫ from 0 to 5 of (k(x) – h(x)) dx.
(c)
• 1 mark: States that using a single integrand (e.g. h(x) – k(x)) would produce negative area on the interval where k(x) is above h(x), giving an incorrect result.
Total: 6 marks.

