Comparing distributions graphically helps reveal meaningful similarities and differences between independent samples by focusing on shape, center, variability, and unusual features visible in visual representations.

Graphical Comparisons of Quantitative Distributions

Graphical displays allow statisticians to compare two or more independent samples by visually examining essential characteristics of their distributions. The AP Statistics curriculum emphasizes selecting appropriate graphs—such as histograms and side-by-side boxplots—to understand how groups differ or resemble each other across key aspects including center, variability, and unusual features like outliers or gaps. Effective graphical comparison requires careful attention to how each display summarizes and communicates quantitative information.

Choosing Appropriate Graphical Representations

Selecting the correct graph is crucial when examining differences among distributions. Each display highlights distinct features of the data, and students must match the graph to the comparison goal.

Histograms for Distribution Shape

Histograms are particularly useful when the goal is to understand the shape of the distributions. By dividing data into intervals and representing frequency with bar height, histograms emphasize:

• The overall shape of each distribution (symmetry, skewness, modality)

• How the data are spread across values

• General patterns of clustering or spacing

Because histograms group values into bins, they help reveal distributional patterns, but they do not show exact data values.

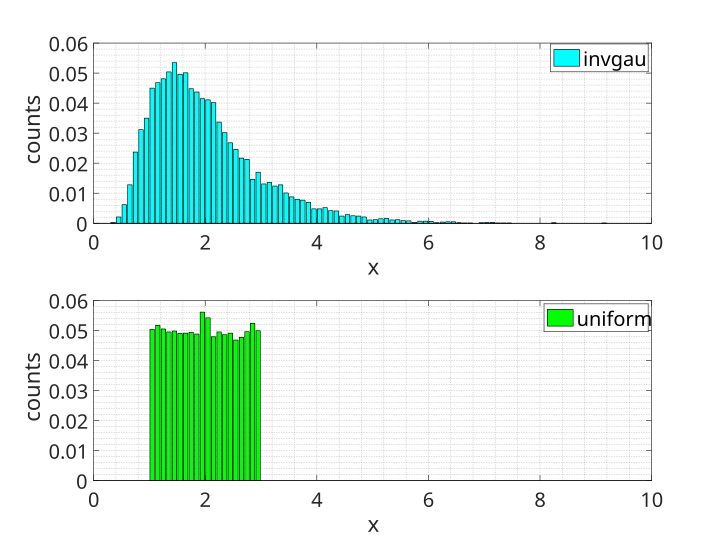
Two histograms display distributions of inverse Gaussian and uniform models over the same range, highlighting pronounced differences in shape and spread. The contrasting bar heights reveal how one distribution clusters while the other remains evenly dispersed. Although labeled with specific probability models, the visual comparison directly supports understanding how histograms reveal differences between groups. Source.

When using histograms for comparison:

• Ensure both samples use the same bin width and common scale

• Compare the prominent features of each distribution’s outline

• Note whether distributions have similar or different degrees of skewness

Side-by-Side Boxplots for Center and Spread

Side-by-side boxplots provide a compressed summary of each dataset and are ideal for comparing center, variability, and overall range. Boxplots rely on the five-number summary (minimum, Q1, median, Q3, maximum), allowing quick identification of structural differences.

Key comparisons visible in boxplots:

• Median position, indicating differences in central tendency

• Interquartile range (IQR), reflecting variability within the middle 50%

• Whisker length, showing the spread of the overall distribution

• Potential outliers, marked with special symbols outside the whiskers

• Relative symmetry, inferred from median placement within the box

Side-by-side boxplots are especially effective for comparing groups because they standardize visual structure, making differences immediately perceptible.

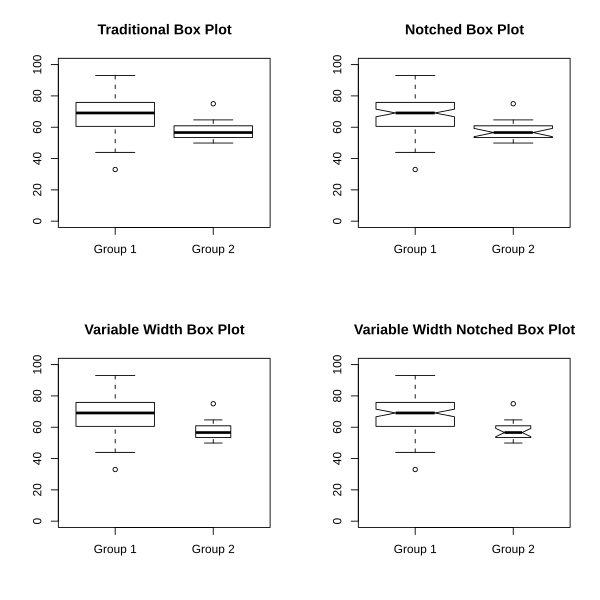
Four paired boxplot displays illustrate how different boxplot styles compare two distributions while emphasizing center, spread, and potential outliers. Each variant presents the same datasets, reinforcing how standardized formats aid visual comparison. Notches and width adjustments exceed syllabus requirements but help students recognize common real-world boxplot variations. Source.

Core Aspects to Compare Across Distributions

Graphical comparisons in AP Statistics emphasize four major distributional features: center, variability, shape, and unusual characteristics. Each contributes to a complete comparative analysis.

Comparing Centers

The center of a distribution—typically represented visually by the median in boxplots or the peak region in histograms—helps determine which group tends to have larger or smaller values.

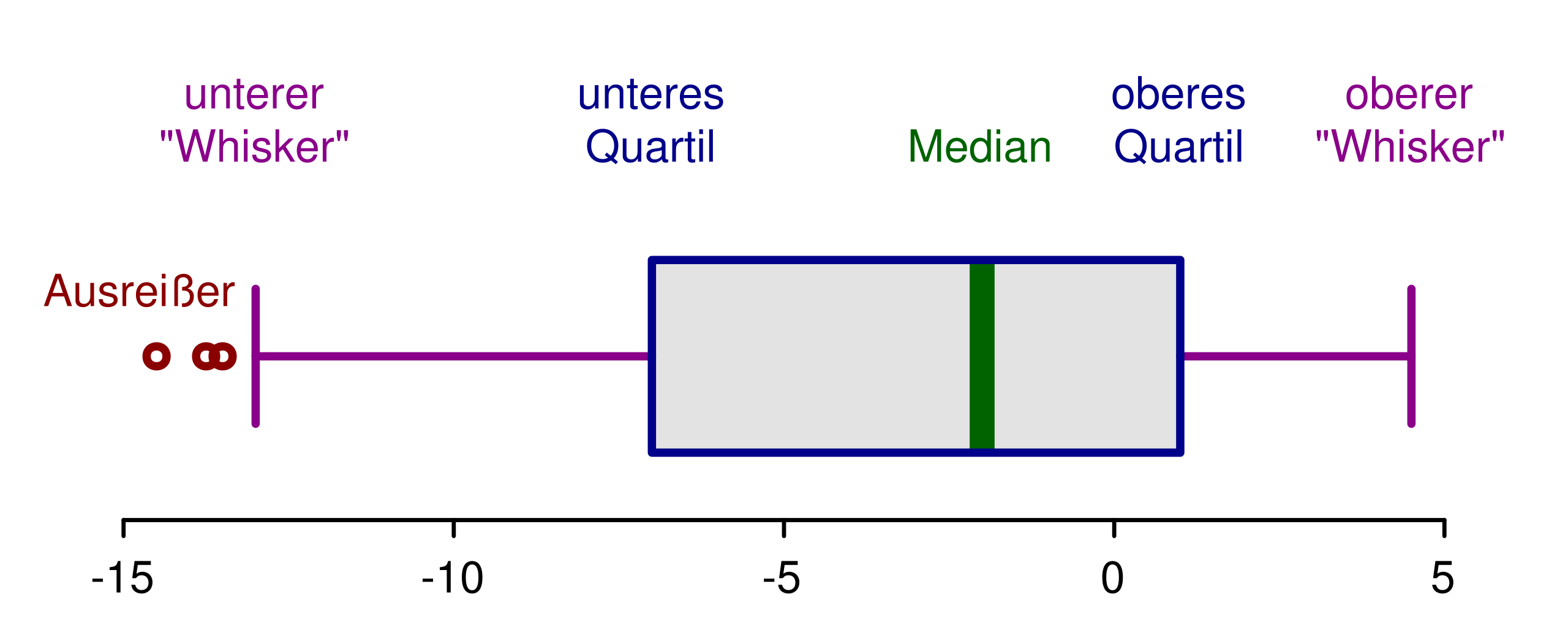
An annotated boxplot labels each component of the five-number summary, demonstrating how boxplots display central tendency and spread. The marked median and quartiles show where data concentrate and how values vary across the distribution. Its precise labeling supports interpreting boxplots before comparing multiple groups. Source.

Students should look for:

• Higher or lower medians in boxplots

• The approximate level of concentration in histogram peaks

• Whether one sample consistently trends above or below the other

Comparing Variability

Variability indicates how spread out data values are within each distribution. Graphs reveal variability through:

• Width of the box in a boxplot (IQR)

• Length of whiskers, representing the overall spread

• Range of bars in a histogram, showing how far values extend

When one group has much greater variability, its distribution appears more stretched or dispersed.

Comparing Distribution Shape

The shape of a distribution influences how data should be interpreted and compared. In graphical comparisons, shape differences may involve:

• Symmetry versus skewness

• Unimodality or multimodality, revealed in histograms

• Clusters, shown as concentrated groups of bars or visible segments

• Gaps, where no data values appear

Shape differences can suggest varying underlying processes or population characteristics.

Identifying Unusual Features

Unusual features add important context to distribution comparisons. These include:

• Outliers, which may distort measures like the mean and standard deviation

• Gaps, indicating missing intervals of data

• Clusters, suggesting subgroups within a sample

• Multiple peaks, revealing structural complexity in the distribution

Careful attention to such features enriches interpretations and prevents misleading conclusions.

Interpreting Graphical Comparisons Effectively

Once graphs are chosen and features identified, students must articulate clear, context-specific comparisons. Effective interpretation should include:

• Explicit statements about which group has the higher center

• Observations on which group shows greater variability

• Notes on shape differences, especially skewness or modality

• Identification of outliers and discussion of their implications

Well-supported claims rely on visual evidence rather than numerical calculations when working exclusively with graphical displays.

Using Visual Representations to Communicate Findings

Graphical comparisons provide accessible, immediate insights into group differences. They help justify claims by showing patterns clearly aligned with context. By focusing on center, spread, shape, and unusual features, AP Statistics students gain skill in examining multiple distributions and drawing accurate, data-informed conclusions directly from visual summaries.