Comparing distributions numerically provides a structured way to evaluate differences in center and variability across independent samples, strengthening interpretations and supporting justified, context-aware statistical claims.

Numerical Comparisons of Distributions

Numerical comparisons focus on using summary statistics—numeric measures describing aspects of a dataset—to contrast two or more independent quantitative distributions. These comparisons complement graphical methods by providing precise, quantitative evidence that supports claims about how distributions differ. In AP Statistics, students are expected to interpret and communicate these comparisons clearly, drawing on measures of center, spread, and relative variability to justify conclusions in context.

Side-by-side boxplots displaying distributions from five independent experiments, highlighting differences in medians and spreads that support numerical comparisons of center and variability. Source.

Measures of Center for Comparison

When comparing distributions, the mean and median serve as the primary indicators of central tendency. The mean is appropriate when data are reasonably symmetric and free from extreme values, while the median is a more resistant measure of center, meaning it is less affected by outliers or skewed distributions.

Using these measures allows students to determine which distribution tends to have higher or lower typical values, forming the foundation of comparative statements. A larger mean or median suggests that observations in one sample generally fall above those of another, but the validity of this comparison depends on the shape and variability of each distribution. Evaluating center alone is insufficient, making measures of variability essential components in comparative analysis.

Measures of Variability for Comparison

Variability indicates how spread out data values are within each distribution. Key measures include the range, interquartile range (IQR), and standard deviation, each highlighting a different aspect of spread. The range captures overall spread but is highly sensitive to extreme values. The IQR measures the spread of the central 50% of the data, making it resistant and useful when data contain outliers or skewness. Standard deviation reflects the average distance of data values from the mean and is especially informative when distributions are roughly symmetric.

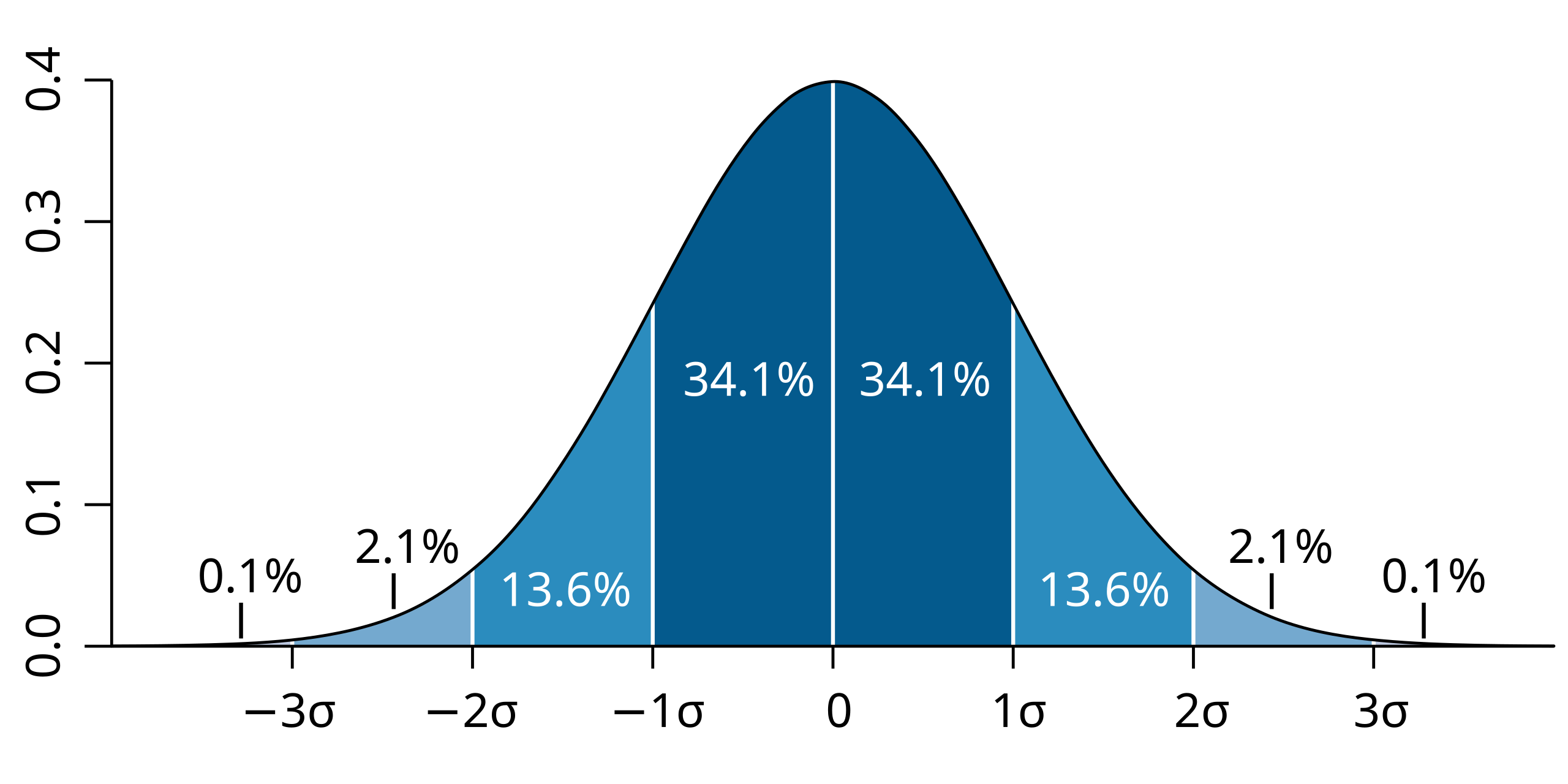
A normal distribution visualizing distances of one, two, and three standard deviations from the mean, reinforcing how standard deviation measures spread around the mean in symmetric distributions. Source.

Numerical comparisons of variability help determine whether one sample exhibits greater consistency or wider dispersion than another. A larger standard deviation or IQR indicates a more variable distribution. These comparisons are crucial because two distributions may share similar centers but differ meaningfully in how spread out the data are.

Using Nonresistant and Resistant Statistics in Comparisons

Choosing appropriate statistics depends on distribution characteristics. Nonresistant statistics, such as the mean, range, and standard deviation, are influenced by outliers and skewness. Resistant statistics, including the median and IQR, provide more stable comparisons when data depart from symmetry.

Effective numerical comparison requires evaluating which statistics best capture meaningful differences given the nature of the data. For example, if one distribution is heavily skewed, comparing medians and IQRs may offer more reliable insight than comparing means and standard deviations. Numerical comparisons should therefore be grounded in an understanding of each distribution’s shape and unusual features.

Communicating Numerical Comparisons

Clear communication is central to this subsubtopic. Students must be able to explain how differences in center and variability support claims about distributions in context. This involves articulating whether one sample tends to have higher typical values, exhibits greater spread, or displays more consistency. Contextual interpretations demonstrate understanding of what numeric differences imply about real-world phenomena.

When presenting comparisons, effective communication includes:

• Identifying which summary statistics were used and why they are appropriate.

• Describing differences in measures of center, such as noting which sample has a larger mean or median.

• Discussing differences in spread, referencing standard deviation, IQR, or range as needed.

• Embedding all comparisons within the context of the data to ensure meaningful interpretation.

• Justifying conclusions by connecting numerical differences directly to the question or claim being addressed.

Integrating Center and Variability in Comparative Claims

Meaningful comparisons typically integrate both center and variability, as considering only one dimension can produce misleading or incomplete conclusions. For example, one distribution may have a higher mean but also substantially greater variability, suggesting less consistency despite a higher typical value. Conversely, a distribution with lower variability may indicate more predictable outcomes even if its center is lower.

Numerical comparisons allow students to articulate multi-dimensional insights, such as:

• Whether differences in center are practically important given the amount of variability.

• Whether distributions overlap substantially or remain distinct based on their spreads.

• How differences in variability might influence decision-making or interpretation.

Understanding these relationships strengthens students’ ability to construct well-justified statistical arguments, aligning with Skill 2.D, which emphasizes selecting and interpreting appropriate numerical summaries to compare independent samples.